Funkcje: potęgowa, wykładnicza i logarytmiczna

Funkcja wykładnicza.

Zad.1. Wyznaczyć dziedziny funkcji :

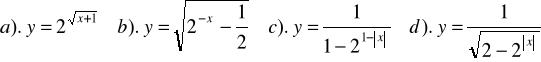
Zad.2. Podać wzór funkcji, której wykres jest symetryczny do wykresu funkcji
względem osi OX .

Zad.3. Podać wzór funkcji, której wykres jest symetryczny do wykresu funkcji
względem osi OY .

Zad.4. Podać wzór funkcji, której wykres jest symetryczny do wykresu funkcji
względem początku układu współrzędnych.

Zad.5. Sprawdzić czy dana funkcja jest parzysta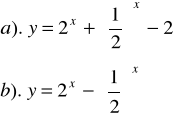

Zad.6. Sporządzić wykres funkcji :

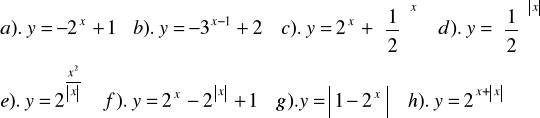
Zad.7. Rozwiązać równania :

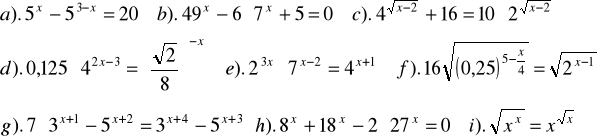
Zad.8. Rozwiązać równanie :

Zad.9. Rozwiązać nierówność :

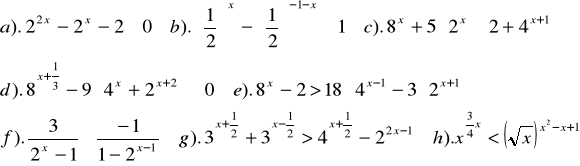
Zad.10. Rozwiązać nierówność :

Zad.11. Rozwiązać układ równań :

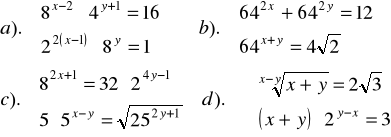
Zad.12.Dane są funkcje

Rozwiązać nierówność :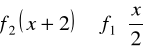
.

Zad.13. Wyznaczyć największą liczbę x , dla której jest spełnione równanie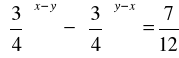
i nierówność :
.

Zad.14. Dla jakich wartości parametru m. równanie :

ma dwa pierwiastki różnych znaków ?

Funkcja logarytmiczna.

Zad.1. Obliczyć na podstawie definicji logarytmu :

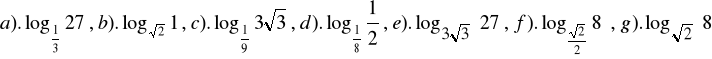
Zad.2. Obliczyć

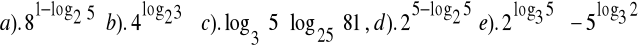
Zad.3. Obliczyć

Zad.4. Uprościć wyrażenie :

Zad.5.

a). Wiedząc, że
obliczyć
.

b). Wiedząc, że
i
, obliczyć
.

c). Wiedząc, że
obliczyć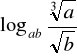
.

Zad.6. Naszkicować wykres funkcji oraz określić dziedzinę, zbiór wartości

i przedziały monotoniczności :

Zad.7. Czym różni się wykres funkcji
od wykresu funkcji
?

Zad.8. Rozwiązać graficznie układy nierówności :

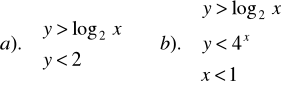
Zad.9. Wyznaczyć dziedzinę funkcji :

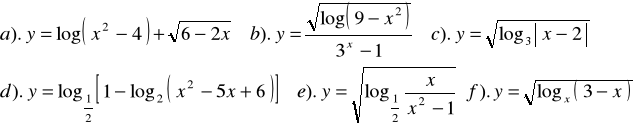
Zad.10. Rozwiązać równania :

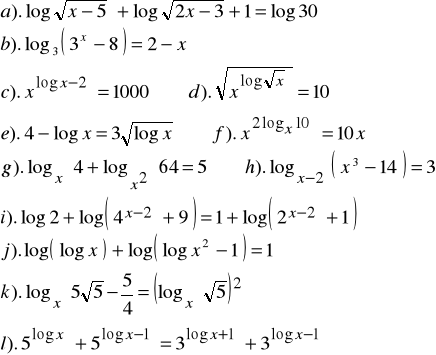
Zad.11. Rozwiązać równanie :

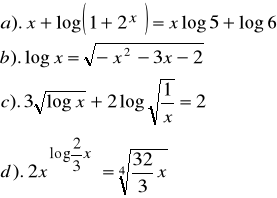
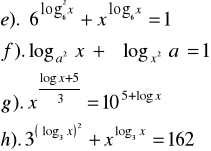
Zad.12. Rozwiązać nierówności :

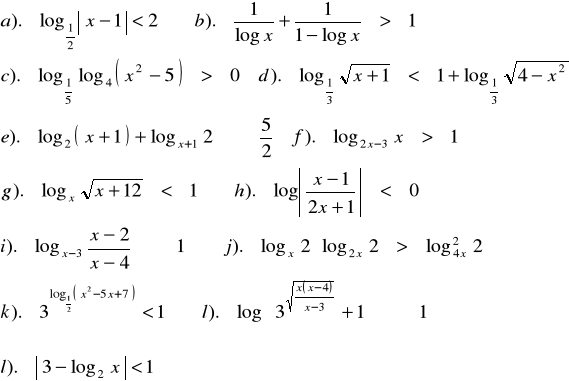
Zad.13. Rozwiązać układ równań :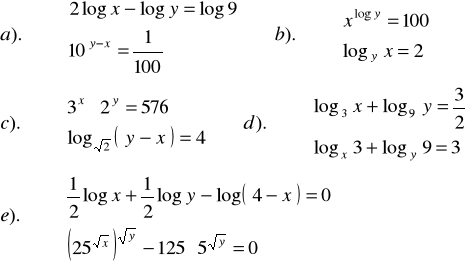

Zad.14. Dla jakich wartości parametru
rozwiązania równania

należą do przedziału
, gdzie

jest rozwiązaniem równania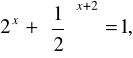
natomiast

rozwiązaniem równania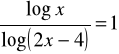
.

Zad.15. Przedyskutować ze względu na parametr
rozwiązalność równania

.

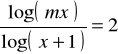
Zad.16. Dla jakich wartości parametru
równanie :

ma dwa różne pierwiastki rzeczywiste ?

Zad.17. Dla jakich wartości parametru
dziedziną funkcji

jest zbiór wszystkich

liczb rzeczywistych ?

Zad.18. Wykazać, że jeżeli
spełnia równanie

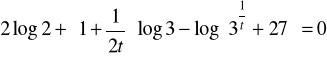
, to nierówność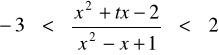
jest prawdziwa dla każdej wartości x.

Zad.19. Dla jakiej wartości parametru
równanie

ma dwa różne pierwiastki ?

Zad.20. Narysować zbiór wszystkich punktów płaszczyzny, których

współrzędne
spełniają nierówność :
.

---