Informacja - podstawy teoretyczne - PRZYKŁADY W PDF 05

Pojęcia wprowadzające

Komunikat - przekaz (mówiony, pisany, radiowy itd), który może przenosić wiadomości

Wiadomość - treść przekazywana przez komunikat (mająca charakter relacji pomiędzy nadawcą i odbiorcą)

• Różne komunikaty mogą przekazywać tą samą wiadomość, np. komunikat: „papież” przekazuje tę samą wiadomość co „biskup Rzymu” czy „głowa kościoła rzymsko - katolickiego”. Wszystkie one identyfikują dla odbiorcy komunikatu tę samą osobę.

• Ten sam komunikat może przekazywać różne wiadomości w zależności różnych uwarunkowań. Np. komunikat „zakwitły kasztany” dla postronnego odbiorcy jest naturalną cechą pory majowej, dla konspiratora zaś może być umownym hasłem informującym o spotkaniu z agentem.

Ogólną własnością komunikatów przekazujących wiadomości jest posiadanie pewnej ilości informacji

uogólniając:

„Komunikatem nazywamy odpowiednio zakodowaną wiadomość, zawierającą pewną ilość informacji”

Dane - taka postać wiadomości, którą można zapisać i/lub przetworzyć z pomocą sprzętu komputerowego, a także - surowe, nie podane obróbce analitycznej liczby i fakty dotyczące zjawisk lub wydarzeń.

Informacja

Termin „informacja” ma charakter interdyscyplinarny. Wywodząc się bezpośrednio z teorii informacji, będącej obszarem szczególnego zainteresowania takich dyscyplin naukowych jak: matematyka , cybernetyka, informatyka czy też elektronika, znajduje swoje miejsce w szeregu innych obszarów nauki, także tych o typowo humanistycznym charakterze.

Pojęcie informacji jest jednym z najtrudniej definiowanych pojęć naukowych. Mimo że każdy intuicyjnie zdaje sobie sprawę z tego, co to jest informacja, to jed­nak jej zdefiniowanie napotyka wiele problemów.

Nie istnieje jedna uznana definicja informacji.

• N. Winer wprowadzając pojęcie informacji stwierdza, że „... Jest ona jak gdyby nazwą treści pochodzącą ze świata zewnętrznego w miarę jak do niego przystosujemy swoje zmysły...”.

• K. Krzakiewicz przez informację rozumie „...przekazywaną przez nadawcę do odbiorcy pewną treść będącą opisem, poleceniem, nakazem, zakazem lub poleceniem.”

• R. Aschby uważa, że „...informacja to przekazywanie różnorodności”.

• W. Głuszkow określa informację „...jako wszelkie wiadomości o procesach i stanach dowolnej natury, które mogą być odbierane przez organy zmysłowe człowieka lub przyrodę..”.

• A.Mazurkiewicz, (cytat za: W.M.Turski, Propedeutyka informatyki, PWN, Warszawa 1985) „Informacją nazywamy wielkość abstrakcyjną, która może być przechowywana w pewnych obiektach, przesyłana między pewnymi obiektami, przetwarzana w pewnych obiektach i stosowana do sterowania pewnymi obiektami, przy czym przez obiekty rozumie się organizmy żywe, urządzenia techniczne oraz systemy takich obiektów.”

• W. Flakiewicz określa informację jako: „... czynnik, który zwiększa naszą wiedzę o otaczającej nas rzeczywistości”.

• Tsitchizris i Lochovsky definiują informację jako „przyrost wiedzy, który może być uzyskany na podstawie danych”

W informatyce przyjmuje się, że informacją nazywamy wielkość abstrakcyjną, która może być przechowywana w pewnych obiektach (np. komputerach), przesyła­na między pewnymi obiektami (np. komputerami), przetwarzana w pewnych obiek­tach (np. komputerach) i stosowana do zarządzania pewnymi obiektami. Obiekt może być komputerem, ale nie musi być nim.

W rozumieniu cybernetyki, informacja jest to: każdy czynnik, dzięki któremu obiekt otaczający go (człowiek, organizm żywy, organizacja, urządzenie automatyczne) może polepszyć swoja znajomość otoczenia i bardziej sprawnie przeprowadzać celowe działanie.

Najbardziej precyzyjna definicja, pochodząca z teorii informacji podchodzi do informacji jako do miary niepewności zajścia pewnego zdarzenia (otrzymania określonego wyniku pomiaru, wyemitowania określonej wiadomości przez źródło) spośród skończonego zbioru zdarzeń możliwych.

Teoria informacji - Dział matematyki na pograniczu statystyki i informatyki dotyczący informacji oraz jej transmisji, kompresji, kryptografii itd. Za ojca teorii informacji uważa się Claude E. Shannona, który w latach 1948-1949 ogłosił fundamentalne prace z tej dziedziny.

Podstawowe założenia ilościowej teorii informacji polega na tym, że komunikat zawiera tym więcej informacji, im mniejsze jest prawdopodobieństwo jego wystąpienia.

Cechy informacji:

• jest niezależna od obserwatora;

• jest różnorodna;

• jest niewyczerpywalna;

• może być powielana w czasie i przestrzeni;

• można ją przetwarzać, nie powodując jej zużycia;

• jest subiektywna - ma inne znaczenie dla różnych odbiorców;

• opisuje obiekt ze względu na tylko jedną jego cechę;

• przejawia cechę synergii (Synergia to współdziałanie różnych czynników, skuteczniejsze niż suma ich oddzielnych działań. Przykładowo: umiejętności kluczowe, nabyte w ramach jednego przedmiotu, skutkują w przypadku pozostałych, pomagając w uzyskiwaniu osiągnięć przez uczniów.)

Ilość informacji

Jednym z podstawowych parametrów opisujących informację zawartą w wiadomości jest jej ilość.

Ustalenie miary informacji jest uzależnione zarówno od podejścia badacza (humanista, fizyk, informatyk). Nadal otwartym pozostaje problem zwartej i uniwersalnej definicji ilości informacji. Można wyróżnić trzy metody określenia miary ilości informacji:

1. podejście uwzględniające strukturalną budowę informacji - uwzględnia się determinowaną budowę masywów informacji. Pomiar tych masywów następuje przez obliczanie elementów informacyjnych (kwantów), tworzących te struktury, albo przez odpowiednie kodowanie masywów.

2. podejście uwzględniające semantyczną wartość informacji - podejście uwzględnia poszczególne cechy informacji takie jak: zasadność, cenność, pożyteczność oraz istotę informacji.

3. podejście uwzględniające zależności statystyczne - operuje pojęciem entropii jako miary nieokreśloności, uwzględniającej prawdopodobieństwo pojawienia się tych lub innych zdarzeń.

Przyjmuje się, że komunikat, którego prawdopodobieństwo wystąpienia wynosi p, zawiera

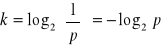
jednostek informacji. Jednostkę informacji nazywa się bitem.

Gdyby równoprawdopodobnych możliwych treści komunikatu było 8, wówczas prawdopodobieństwo każdego z nich wynosiłoby 0,125 i wówczas zgodnie ze wzorem, ilość informacji zawartą w każdym z takich komunikatów wynosiłaby:

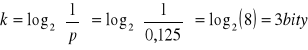
W sytuacji gdy wariantów tych jest mniej, wówczas ilość niezbędnych bitów jest nieco mniejsza (ułamkowa), a tym samym nie realizowalna technicznie. W przypadku zastosowania najmniejszej możliwej ilości bitów do zakodowania wariantów tego komunikatu mamy do czynienia ze zjawiskiem redundancji (patrz dalej).

W praktyce niezmiernie rzadko mamy do czynienia z sytuacjami, w których wszystkie możliwe warianty komunikatu dotyczącego jednej cechy zmiennej losowej są równieprawdopodobne. W dalszym ciągu, zgodnie ze wzorem i z intuicją możemy twierdzić, że wystąpienie wariantu najmniej prawdopodobnego - najmniej oczekiwanego - niesie ze sobą największą porcję informacji, natomiast wystąpienie wariantu najbardziej prawdopodobnego jest najbardziej spodziewane czyli niesie najmniejszą porcję informacji.

W sytuacjach takich, o wysokim stopniu złożoności, szczególnie użyteczną jest miara mówiąca o średniej ilości informacji niesionej przez poszczególne możliwe (ale niekoniecznie równieprawdopodobne) komunikaty. Średnia ta, dla uwzględnienia częstości występowania różnych wariantów komunikatu, powinna mieć charakter średniej ważonej częstością ich występowania.

Entropia

Założenia:

• Aby zdarzenie było charakteryzowane między innymi przez prawdopodobieństwo, musi być zdarzeniem losowym. „Jeżeli zajścia lub niezajścia pewnego zdarzenia nie można przewidzieć, i jeśli powiedzenie, że zachodzi ono lub nie, ma zawsze sens, to mówimy, że takie zdarzenie jest zdarzeniem losowym.”

Jeżeli zdarzenie losowe ma charakter masowy, to prawdopodobieństwo wystąpienia określonych stanów może być zastąpione jego częstością. Dla przykładu, wartość dziennych wpłat i wypłat w danym oddziale banku jest zmienna masową. Ustalenie prawdopodobieństwa wystąpienia określonego poziomu wpłat lub wypłat w danym dniu może być zastąpione wyznaczoną na podstawie analizy danych historycznych częstością jego występowania w przeszłości. Dla odmiany prawdopodobieństwo wystąpienia określonego poziomu wypłat w tymże oddziale banku na drugi dzień po ogłoszeniu problemów z utrzymaniem przez bank płynności nie jest możliwe do oszacowania tą drogą bowiem jest to zdarzenie losowe ale występujące sporadycznie. Szacunek prawdopodobieństwa jest w tym przypadku dokonany przez ekspertów na podstawie ich wiedzy i doświadczania.

• Niech X jest zmienną losową. X1, ..., Xn będą wartościami tej zmiennej (wariantami treści wiadomości) występującymi z prawdopodobieństwem p(X1), ..., p(Xn), przy czym:

• 
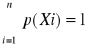
  Entropię dyskretnej zmiennej losowej X (danej wiadomości) definiuje się jako średnią ważoną:

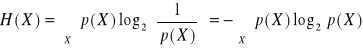
• Entropia jest w efekcie formalną miarą ilości informacji w wiadomości mogącej być wyrażoną różnymi wariantami komunikatu.

Cechy entropii

• Można udowodnić, że dla zmiennych dyskretnych przyjmujących n wartości entropia jest maksymalna w przypadku rozkładu jednostajnego p(X1) = p(X2) = ... = p(Xn) = 1/n, tj. gdy wszystkie warianty wiadomości są jednakowo prawdopodobne i wynosi log n. Dla zmiennych ciągłych największą entropię wśród wszystkich rozkładów o tej samej wariancji posiada rozkład normalny.

• H(X) maleje ze wzrostem nierównomierności wystepowania poszczególnych wiadomości osiągając minimum równe 0 dla p(Xi) = 1 Oznacza to, że przykładowa wiadomość, iż: „w bilansie banku, suma aktywów jest równa sumie pasywów” nie niesie za sobą żadnej informacji, bowiem prawdopodobieństwo tego stanu jest równe jedności (prawdopodobieństwo wszystkich innych stanów jest równe zeru). O ile więc w potocznym rozumieniu stwierdzenie to uznamy za informację wzbogacającą rozumienie otaczających zjawisk, to z punktu widzenia teorii nie jest to informacja.

• Podobnie z resztą, wbrew potocznemu rozumieniu wiadomość ta zasłyszana po raz drugi nie będzie już niosła informacji, bowiem posiadając zdobytą wcześniej wiedzę posiadamy już pewność odnośnie takiego stanu rzeczy.

Kodowanie - dobór języka zapisu informacji

W praktyce poszczególne warianty komunikatu rzadko mogą być wyrażone prostymi krótkimi oznaczeniami literowymi lub cyfrowymi. Dla przykładu zakładając, iż poszczególne słowa używane w języku mówionym są różnymi wariantami komunikatu, mamy do czynienia z różną ich długością.

Jeżeli zakodować poszczególne warianty w sposób bardziej oszczędny, wówczas odbiorca komunikatu, znając sposób kodowania, jest w stanie odtworzyć ich postać pierwotną.

Kod danego komunikatu nazywa się ciągiem albo słowem kodowym komunikatu, a liczba występujących w nim znaków - długością słowa kodowego. W zależności od przyjętej konwencji kodowania mamy do czynienia z kodami o stałej lub zmiennej długości. . Jeżeli jednak do kodowania użyjemy tylko dwóch różnych symboli (np. 0 i 1), to minimalna długość Ni słowa kodowego komunikatu występującego z prawdopodobieństwem pi jest dana wzorem:

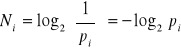
a tym samym jest tożsama ze wzorem na ilość informacji przekazywanej przez komunikat.

Uwzględniając różne prawdopodobieństwo występowania różnych wariantów komunikatu, średnią (ważoną) minimalną długość słowa kodowego wyznaczamy wzorem:

Ilość informacji mierzona entropią jest jednocześnie przeciętną liczbą bitów niezbędnych do zakodowania wszystkich możliwych informacji w optymalny sposób.

Kodowanie Huffmana

Algorytm Huffmana to jeden z najprostszych, jednak niezbyt efektywnych systemów bezstratnej kompresji danych.

Praktycznie nie używa się go samodzielnie, jednak często używa się go jako ostatniego etapu w różnych systemach kompresji, zarówno bezstratnej jak i stratnej.

Algorytm Huffmana to system przypisywania skończonemu zbiorowi symboli o z góry znanych prawdopodobieństwach kodów o zmiennej liczbie bitów. Później symbole te są zastępowane odpowiednimi bitami na wyjściu. Symbole te to najczęściej po prostu bajty, choć nie ma żadnych przeszkód żeby było nimi coś innego.

Algorytm

1. Dla każdego symbolu S tworzymy węzeł o wartości równej prawdopodobieństwu wystąpienia S. Prawdopodobieństwa nie muszą w sumie dawać jedynki, muszą jedynie zachować proporcje, tak więc można równie dobrze używać np. ilości wystąpień danego znaku.

2. Bierzemy 2 wolne węzły z najmniejszymi wartościami (jeśli kilka węzłów ma taką samą wartość bierzemy dowolny z nich) i łączymy je jako 2 podgałęzie nowego węzła. Węzeł ten ma wartość równą sumie wartości obu węzłów.

3. Powtarzamy tak długo dopóki jest więcej niż 1 wolny węzeł.

Kody dla znaków obliczamy w następujący sposób - idąc od ostatniego wolnego węzła - w lewo bit 0, w prawo bit 1.

Redundancja

Redundancja, w teorii informacji nadmiar informacji przekraczający minimum potrzebne do rozwiązania danego problemu lub przekazu tej informacji, np. zapis liczby 1 jako 01,00 jest redundantny.

Innym przykładem redundancji może być przesyłanie daty dziennej i jednocześnie nazwy dnia tygodnia (nazwa dnia jest jednoznacznie określona datą).

Jeśli na przesyłaną wiadomość składa się losowa kombinacja 26 liter alfabetu angielskiego, odstępu i 5 znaków interpunkcyjnych i jeśli założymy, że prawdopodobieństwo każdej takiej wiadomości jest takie samo, to entropia wynosi H = log₂32 = 5. Oznacza to, że potrzebujemy 5 bitów aby zakodować dowolny znak lub wiadomość: 00000, 00001, 00010, ... 11111. Efektywność transmisji lub zapisu (przechowywania) wiadomości wymaga aby zredukować liczbę bitów użytych do kodowania. Jest to możliwe podczas przetwarzania angielskiego tekstu ponieważ występowanie poszczególnych liter nie jest całkowicie przypadkowe. Na przykład prawdopodobieństwo, że literą następującą po ciągu liter INFORMATIO jest "N" jest niezwykle wysokie. Można wykazać, że entropia zwykłego angielskiego tekstu wynosi około jeden bit na literę. Oznacza to, że język angielski (tak jak i każdy inny język) ma wbudowaną bardzo dużą nadmiarowość określaną mianem redundancji.. Redundancja umożliwia np. zrozumienie wiadomości, w której pominięto samogłoski lub odczytanie niestarannego pisma odręcznego. We współczesnych systemach komunikacyjnych, sztuczna redundancja jest wprowadzana w procesie kodowania wiadomości w celu zmniejszenia liczby błędów w transmisji wiadomości.

SZUM INFORMACYJNY I JEGO WPŁYW NA POZIOM RYZYKA

Dotychczasowe rozważania koncentrowały się wokół ryzyka, którego źródłem jest niepewność osiągania wartości oczekiwanych (realizacji celu) przez poszczególne zmienne ekonomiczne. Ich suma składa się na ryzyko rzeczywiste analizowanego systemu ekonomicznego. Dyskutowane wcześniej miary informacji (prawdopodobieństwo, entropia) służyły więc pomiarowi ilości informacji niezbędnej do całkowitego wyeliminowania tej niepewności.

Złożoność analizowanych systemów ekonomicznych nie pozwala często decydentowi na bezpośredni odczyt czynników ryzyka w miejscu w którym występują.

Naturalną sytuacją jest występowanie kanałów informacyjnych, które pośredniczą pomiędzy źródłem danych a jej odbiorcą (Rysunek)

Jego obecność staje się podstawą sformułowania istotnego problemu teorii informacji, dotyczącego kwestii doskonałego przesłania informacji przez niedoskonały kanał informacyjny.6

Kanał informacyjny staje się bowiem źródłem szumu informacyjnego, który dodatkowo powiększa lukę informacyjną związaną z ryzykiem rzeczywistym. W efekcie obserwator narażony jest na ryzyko łączne, będące sumą ryzyka właściwego i szumu informacyjnego (Rysunek).

Przykładami „zaszumianych” kanałów informacyjnych mogą być np.: dla właściciela firmy - uproszczone sprawozdania finansowe, dla inwestora giełdowego - niepełna lub przekłamana informacja o czynnikach kształtujących kurs spółki, dla posiadacza jednostek uczestnictwa - uproszczona informacja o strategii inwestycyjnej funduszu itd.

Szum informacyjny może powodować zarówno zawyżenie ryzyka postrzeganego w stosunku do rzeczywistego, jak również jego zmniejszenie.

W obydwu przypadkach istotnym jest, iż o ile cena za oczekiwany dochód wynika z poziomu ryzyka postrzeganego, o tyle oczekiwany dochód z inwestycji wiąże się z istniejącym ryzykiem rzeczywistym.7

Systemowe lub incydentalne zakłócenia w procesie pozyskiwania informacji na temat zachodzących procesów prowadzić mogą do istotnego przekłamania oceny ryzyka i jego ekonomicznych skutków.

Informacja w procesie zarządzania

Jest związana z realizacją funkcji zarządzania (planowanie, organizowanie, przewodzenie i kontrolowanie) oraz pozwala na podjęcie decyzji na różnych szczeblach zarządzania.

Grupy informacji dla zarządzania:

• pokrzepiająca - dotyczy sytuacji bieżącej, jej celem jest zapewnienie, że wszystko przebiega zgodnie z przyjętymi założeniami;

• rozwojowa - ocena stanu (przebiegu) zjawiska lub procesu; ewentualnie pokazanie trudności;

• ostrzegawcza - sygnalizuje, iż wystąpiły określone zagrożenia w wyniku realizacji działalności organizacji lub też, że mogą one niebawem wystąpić;

• planistyczna - odnosząca się do poziomu lub stanu przyszłego zjawiska lub procesów gospodarczych;

• operacyjna - określa działanie własnej organizacji i umiejscawia ją na mapie jej podobnych;

• opiniodawcza - dotyczy otoczenia organizacji;

• kontrolna - przekazywana otoczeniu (banki) o działalności organizacji.

Informacja zawarta w sprawozdaniach finansowych firmy

• Złożoność wewnętrznych mechanizmów funkcjonowania, jak również występowanie szeregu zmiennych egzogenicznych o bardzo ograniczonej przewidywalności sprawiają, że skutek podejmowanych działań może być również przewidywany wyłącznie z pewnym, z reguły niewielkim prawdopodobieństwem. Z tego też względu wiadomość o finansowych efektach danego przedsięwzięcia gospodarczego, zawarta na przykład w sprawozdawczości banku, niesie za sobą ogromną ilość informacji o decydującym znaczeniu dla każdego analityka.

• W zależności od przeznaczenia zróżnicowany będzie zarówno charakter jak i poziom jej szczegółowości. Nie ulega jednak wątpliwości, iż informacja dostarczona przez mechanizmy rachunkowości stanowi podstawę oceny aspektów finansowych funkcjonowania instytucji bankowej.

• Różna będzie też ilość informacji w sprawozdaniu dla różnych odbiorców

System informacyjny w systemowym modelu przedsiębiorstwa

• Traktując dowolne przedsiębiorstwo z punktu widzenia podejścia systemowego, możemy traktować je jako obiekt gospodarczy - otwarty, dynamiczny układ społeczno-techniczny, realizujący określone cele gospodarcze. W jego ramach można wyróżnić dwa podstawowe podsystemy: system zarządzania oraz system działalności podstawowej. Coraz częściej, wobec wzrastającego znaczenia informacji jako podstawowej determinanty sukcesu firmy wyodrębnia się system informacyjny jest jako odrębny, równoprawny system.

• Pomiędzy poszczególnymi systemami obiektu gospodarczego mają miejsce różnorodne przepływy o charakterze rzeczowym (przepływy zasileniowe) lub też informacyjnym. Proporcja pomiędzy tymi dwoma kategoriami przepływów zależy głównie od charakteru przedsiębiorstwa (produkcyjne, usługowe) oraz od stopnia skomplikowania działalności (handel detaliczny, usługi bankowe).

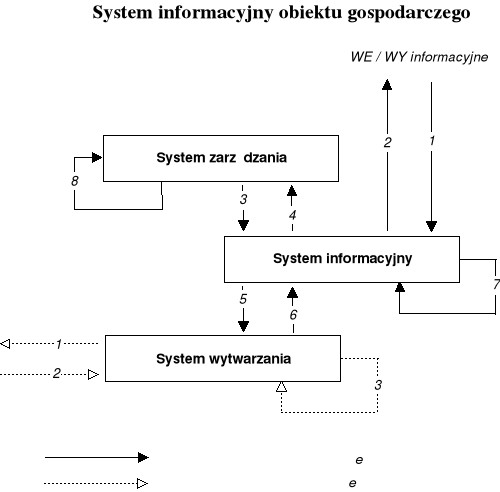
źródło: Praca zbiorowa pod redakcją Adama Nowickiego, Podstawy informatyki dla ekonomistów, Wydawnictwo Naukowe PWN, Warszawa 1995, s.16

• W przypadku przedsiębiorstwa bankowego na przepływy zasileniowo - rzeczowe składają się (oprócz marginalnych ilościowo i wartościowo działań w ramach gospodarki własnej banku) przede wszystkim czynności związane z obsługą obrotu gotówkowego. Działalność banku w zakresie obrotu gotówkowego jest wielokrotnie mniejsza od działalności w zakresie obrotu gotówkowego. Ponieważ pieniądz żyrowy ma w zasadzie postać zapisu informacyjnego na rachunku bankowym (realizowanego jedynie różnymi środkami technicznymi), dlatego też można w dużym uproszczeniu scharakteryzować bank jako przedsiębiorstwo zajmujące się w dużej mierze przetwarzaniem informacji. Z tego względu, decydującą rolę w obiekcie bankowym odgrywają przepływy o charakterze informacyjnym.

• Indywidualnego podejścia wymaga definicja bankowego „systemu wytwarzania”. W przypadku każdego przedsiębiorstwa powinien on reprezentować jego podstawową - pozainformacyjną - sferę działalności. Dla banku będzie to w dużej mierze sfera obsługi klienta.

• Szczególne znaczenie systemu informacyjnego przedsiębiorstwa bankowego wynika z wyjątkowej złożoności oraz niezwykle dużej (w porównaniu z innego typu podmiotami) ilości występujących przepływów informacyjnych. Wielokrotnie schemat obiegu informacji w banku jest utożsamiany z jego strukturą organizacyjną bądź też przynajmniej ze strukturą systemu informatycznego. Podejście to znajduje swoje uzasadnienie w znacznym powiązaniu i uzależnieniu tych struktur z wymogami informacyjnymi banku.

Wybrane implikacje dla SIZ:

• Scentralizowana struktura wymaga przepływu pionowego informacji i vice versa

• SIZ muszą być dostosowane do potrzeb poszczególnych zespołów, działów i obszarów funkcjonalnych

• System dostosowany do potrzeb danego przedsiębiorstwa

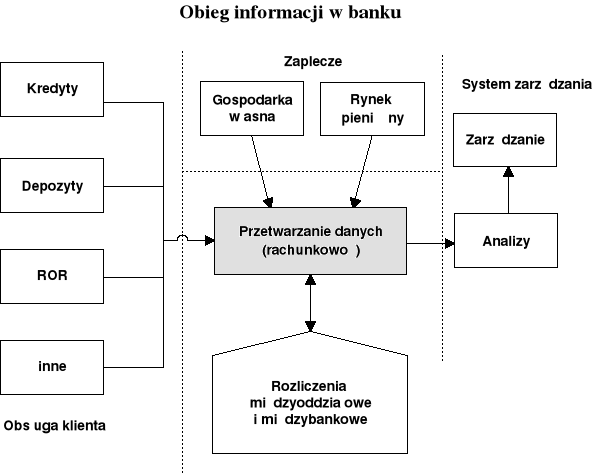
źródło: Adam Pawełczak, Informatyka bankowa, Wydawnictwo WSB, Poznań 1995, s.10

Cechy nowoczesnego przedsiębiorstwa

Elastyczne i szczupłe

• zdolne do szybkich inwestycji i dezinwestycji, mało zintegrowane, o małych kosztach stałych, zarządzane przez projekty i struktury macierzowe,

Kooperatywne

• poszukujące współdziałania a nie konkurencji, zawiązujące liczne umowy z dostawcami i nabywcami oraz alianse z konkurentami w celu budowy pełnej oferty bez własnych zasobów,

Inteligentne

• mające rozbudowane zasoby intelektualne a nie materialne, inwestujące w pracowników oraz badania i rozwój, dysponujące wywiadem ekonomicznym i sprawnie działającym kontrolingiem.

Fazy zarządzania wiedzą

• Nabywanie wiedzy

• Dzielenie się wiedzą

• praca w ramach projektu specjalistów z różnych podsystemów organizacji i o różnej wiedzy,

• dyskusje i grupowe rozwiązywanie problemów,

• codzienna współpraca zespołów z danej dziedziny np. w formie zespołów innowacyjnych czy laboratoriów,

• alianse z konkurentami i dostawcami, dzięki którym następuje transfer wiedzy z nieznanych nam sektorów, rynków i technologii.

• Przekształcanie wiedzy w decyzję

• formy i procedury decyzyjne umożliwiające zaangażowanie w proces decyzyjny najbardziej kompetentnych ludzi. Nie oznacza to zespołowej formy decyzji, ale wykorzystanie najlepszych kadr w procesie zbierania informacji, formułowania rozwiązań, doboru kryteriów, symulacji skutków każdego z wariantów,

• sprawnie działający i dostosowany do potrzeb określonych decydentów system wywiadu gospodarczego lub inny system wspomagający decyzje,

• systemy oceny i wynagradzania menadżerów promujące nowatorskie i śmiałe rozwiązania i wydłużające okres oceny, aby unikać decyzji koniunkturalnych .

T.Gerstenkorn, T.Śródka, „Kombinatoryka i rachunek prawdopodobieństwa”, Państwowe Wydawnictwa Naukowe, Warszawa 1980, s.57

1

---