PRACOWNIA FIZYCZNA A.P. W SIEDLCACH
Agnieszka Kisielińska, Matematyka III, dzienne Imię i nazwisko, kierunek studiów			Grupa IV
Numer ćwiczenia 62	Data wykonania 7 marca 2000	Ocena zaliczenia	Podpis

Temat: Wyznaczanie współczynnika temperaturowego oporu

Temperatura [ °C ]		Pomiar oporu Rx [ Ω ]		Współczynnik temperaturowy oporu α [ 1/°C ]
t1	t2	Rt1	Rt2	α	α1/2	αśr
22 30 35 40 45 50 55 60 65 70 75 80 85 90	30 35 40 45 50 55 60 65 70 75 80 85 90	4800 3000 2550 2060 1720 1550 1430 1120 920 740 600 530 480 420	3000 2550 2060 1720 1550 1430 1120 920 740 600 530 480 420	- 0,023077 - 0,015780 - 0,016388 - 0,014226 - 0,010462 - 0,010462 - 0,012264 - 0,011363 - 0,011043 - 0,010370 - 0,008485 - 0,008054 - 0,008434	- 0,0146668	- 0,0123398
											- 0,00962487

Wielkością charakteryzująca zmiany temperaturowe oporu przewodnika jest współczynnik temperaturowy oporu. Wyraża on względny przyrost oporu *R/R przy ogrzaniu przewodnika o 1°C. Jeśli przyrost oporu *R jest spowodowany ogrzaniem od 0 do t stopni, to współczynnik α możemy określić zależnością:

α =
=
,

ale w naszym doświadczeniu nie znamy wartości R₀, ale znając opory tego przewodnika w temperaturach t₁ i t₂

możemy posłużyć się wzorem na współczynnik α wyprowadzonym następująco

R_t = R₀ ( 1 + α t ),

Mając opory R₁ i R₂ tego samego przewodnika w temperaturach t­­­₁ i t­₂ uzyskujemy dwa równania

R₁ = R₀ ( 1 + α t₁ )

R₂ = R₀ ( 1 + α t₂ )

Rozwiązując układ równań otrzymujemy wzór na α jako funkcję α ( R₁, R₂, t₁, t₂ )

α =
(1)

Pomiary oporów R₁ i R₂ przeprowadzamy za pomocą układu liniowego mostka Wheastone'a.

Schemat mostka Wheastone'a

Po podstawieniu odpowiednich wartości do wzoru (1) otrzymujemy wartości zapisane w tabeli. Poszczególne α otrzymaliśmy dla wartości R1 i R2 przy temperaturach t1 i t2 których różnica wynosi 5 °C

Wartości średnie α:

- w temperaturze 22 °C - 55 °C α = - 0,0146668 [ 1/°C ]

- w temperaturze 60 °C - 90 °C α = - 0,00962487 [ 1/°C ]

- w całym przedziale temperatury α = - 0,0123398 [ 1/°C ]

Rachunek błędów:

*R = 10 Ω

*t = 1 °C

Błąd *α obliczamy metodą różniczki zupełnej traktując α jako funkcję α ( R₁, R₂, t₁, t₂, ). Obliczenia błędów robimy dla każdego α, jak wyżej obliczaliśmy samo α.

*α =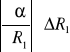
+
+
+

=

=

=

=
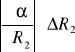
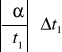
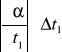
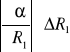
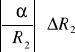
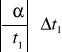
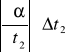
, a po podstawieniu wartości otrzymujemy:

*α₁ = 0,00027944 Ω *α₂ = 0,000116675 Ω *α₃ = 0,000932364 Ω *α₄ = 0,000746821Ω *α₅ = 0,00050924 Ω *α₆ = 0,000404849 Ω *α₇ = 0,000361646 Ω *α₈ = 0,000232091 Ω *α₉ = 0,00014302 Ω

*α₁₀ = 0,0000108729 Ω *α₁₁ = 0,000414271 Ω *α₁₂ = 0,000568111 Ω *α₁₃ = 0,000472925 Ω

Uwagi i wnioski:

Celem doświadczenia jest wyznaczenie współczynnika temperaturowego oporu. Opór jest stały dla danego przewodnika tylko wówczas gdy nie zmienia się jego temperatura. Przy ogrzewaniu lub oziębianiu przewodnika obserwuje się odpowiednio przyrosty dodatnie lub ujemne oporu *R, tym większe im większy jest przyrost temperatury *t. Dla każdego przewodnika charakterystyczny jest jego współczynnik temperaturowy oporu

α =
. Substancje dla których α < 0 to niemal wszystkie metale, półprzewodniki i elektrolity charakteryzują się tym, że α > 0, a α ≅ 0 posiada nieliczna grupa stopów.