MECHANIKA PŁYNÓW

1. Płyn - substancja, która może płynąć (=ciecze i gazy).
   

1. Jeżeli na płyn działa siła powierzchniowa, to musi być prostopadła do powierzchni płynu (styczna =warstwy ślizgają się powierzchni, bo płyn nie może zrównoważyć siły stycznej. Wynika z tego zdolność płynu do zmiany kształtu i płynięcia)
   

2. W świetle powyższych faktów wygodnie jest wprowadzić wielkość opisującą siłę działającą na płyn, uwzględniającą szczególny kierunek tej siły ⇒ CIŚNIENIE.

Ciśnienie - wartość prostopadłej siły (F), przypadającej na jednostkę powierzchni (s)

Związek pascala z innymi jednostkami ciśnienia (spoza układu SI):

1 atm = 760 mm Hg = 101325 Pa;

(atmosfera) (milimetry słupa rtęci)

(ciśnienie jest wielkością skalarną; jest przekazywane bez zmian na sztywne ścianki naczynia, wszystkie przekroje prostopadle do nich)

3. Gęstość ciała (substancji) - stosunek masy tego ciała (m) do jego objętości (V)

gęstość (=masa właściwa) jest wielkością skalarną; zależy m.in. od temperatury i ciśnienia; dla cieczy zmienia się nieznacznie, dla gazów -bardzo silna zależność.

4. Ciężar właściwy - stosunek ciężaru tego ciała (Q) do jego objętości (V)

ciężar właściwy jest wielkością wektorową (wektor zgodny z wektorem ciężaru)

5. Zmiany ciśnienia wewnątrz nieruchomego płynu

Ciśnienie hydrostatyczne - ciśnienie panujące w płynie będącym w spoczynku; jest to ciśnienie, jakie wywiera słup płynu o wysokości h i gęstości d (g- przyspieszenie ziemskie g ≈ 10m/s²)

a) ciecze - są nieściśliwe, a więc zależność od wysokości h jest liniowa:
,

gdzie p_o = 1,013⋅10⁵ Pa - ciśnienie atmosferyczne (=normalne)

b) gazy - są ściśliwe, a więc zależność od wysokości h jest nieliniowa:
gdzie d_o = 1,2kg/m³ - gęstość powietrza w
warunkach normalnych; g(d₀/p₀) = 0,116 km^-1

6. Prawo Pascala: Ciśnienie wywierane na zamknięty płyn jest przekazywane jednakowo na każdą część płynu oraz na ścianki naczynia bez żadnych strat (nie obowiązuje, gdy brak równowagi w cieczy, np. fala dźwiękowa).

7. Prawo Archimedesa: Ciało w całości lub częściowo zanurzone w płynie wypierane jest ku górze z siłą równą ciężarowi płynu (Q_pl) wypartego przez to ciało.

[N], gdzie m_pl - masa wypartego płynu,

d_pl - gęstość wypartego płynu,

V_pl - objętość wypartego płynu,

V_cz.zan. - objętość części zanurzonej ciała,

g - przyspieszenie ziemskie

siła wyporu = statyczna siła nośna

8. Warunek pływania:

Mówimy, że ciało pływa, jeśli nie zanurza się i nie wynurza. Oznacza to, że wszystkie siły działające w pionie na ciało muszą się równoważyć. I tak: warunek pływania dla ciała unoszącego się na powierzchni płynu przyjmie postać:

(siła wyporu = ciężar ciała)

9. Charakterystyka przepływu - opis ruchu płynu poprzez określenie jego gęstości i prędkości w każdym punkcie przestrzeni i w każdej chwili czasu.
   

10. Ciecz idealna = nieściśliwa i nielepka !!!

11. Cechy przepływu idealnego:
    a) ustalony (laminarny) - prędkość płynu jest w dowolnie wybranym punkcie stała w czasie (każda cząsteczka płynu przepływając przez ten punkt będzie miała przypisaną temu punktowi prędkość)
    b) bezwirowy - w żadnym punkcie element płynu nie ma względem tego punktu wypadkowej prędkości kątowej.

c) nieściśliwy - (np. ruch powietrza wzgl. skrzydeł samolotu lecącego z prędkością dużo mniejszą od
prędkości dźwięku w powietrzu - aerodynamika poddźwiękowa w gazie, dowolny ruch w cieczach)
d) nielepki - lepkość w ruchu płynu jest odpowiednikiem tarcia w ruchu ciał stałych (tarcie występuje między powierzchniami tych ciał, a lepkość - między warstwami płynu); powoduje pojawienie się sił stycznych między warstwami płynu, poruszającymi się wzgl. siebie. Efektem występowania lepkości są straty energii mechanicznej.

12. Równanie (=Prawo) ciągłości (strugi) - zwane też prawem zachowania masy dla płynów
    

gdzie Δm/Δt - strumień masy,

S - powierzchnia przekroju strugi,

v - prędkość przepływu,

d_pl - gęstość płynu,

S⋅v - strumień objętościowy lub natężenie przepływu

Dla nieściśliwego przepływu ustalonego prędkość płynu zmienia się odwrotnie proporcjonalnie do pola powierzchni przekroju. Iloczyn ten pozostaje stały wzdłuż strugi prądu (linii prądu) - oznacza to, że jeśli mamy do czynienia z węższą częścią strugi (= mniejszym przekrojem), to linie prądu są tam zagęszczone, a więc prędkość przepływu jest większa.

14. Równanie (=Prawo) Bernoulliego - jest spełnione dla przepływu nielepkiego, nieściśliwego i ustalonego (występujące w równaniu wielkości powinny być obliczone wzdłuż linii prądu); mówi, że w dowolnym punkcie przepływu (spełniającego powyższe warunki) suma ciśnień statycznego, hydrostatycznego i dynamicznego jest wielkością stałą.

, gdzie p_st - ciśnienie statyczne; ,

p_h - ciśnienie hydrostatyczne,

p_d - ciśnienie dynamiczne

, v - prędkość przepływu,

d_pl - gęstość płynu,

g - przyspieszenie ziemskie

h - wysokość (/położenie) rozważanego punktu w płynie nad poziomem odniesienia

Jeśli w płynie w dwóch miejscach wystąpi różnica prędkości przepływu (prędkość v₁ w punkcie A będzie większa niż v₂ w punkcie B), to w efekcie otrzymamy różnicę ciśnień dynamicznych (p_dA> p_dB), a żeby suma wszystkich ciśnień dawała tę samą liczbę w każdym z punktów - ciśnienia statyczne (p_st+ p_h) będą się różnić o dokładnie taką samą wartość jak dynamiczne, tylko (p_stA + p_hA) < (p_stB +p_hB ). Ponieważ różnica ciśnień zawsze wywołuje przepływ od wyższych ciśnień statycznych do niższych (a przynajmniej dążenie do wyrównania ciśnień), cząsteczki płynu, przepływając będą parły z siłą F_n na każdą napotkaną powierzchnię S. Otrzymujemy w ten sposób zależność:

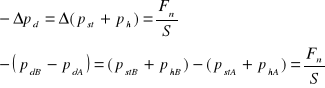
Siłę F_n nazywamy (dynamiczną) siłą nośną. Jest ona prostopadła do powierzchni S.

Zjawisko takie obserwuje się przy ruchu ciał w płynie, gdy następuje nierównomierny podział strugi na części nad- i pod ciałem. Z jednej strony ciała przepływa więcej warstw niż z drugiej, a co za tym idzie ich prędkość przepływu musi być większa niż tam, gdzie tych warstw jest mniej. Wywołana w ten sposób różnica ciśnień powoduje powstanie (dynamicznej) siły nośnej. Wspomniany nierównomierny podział strugi pojawi się, gdy poruszające się w płynie ciało jest niesymetryczne jak np. skrzydło samolotu (rys.1) lub gdy ciało jest wprawdzie symetryczne, lecz obraca się wokół osi prostopadłej do kierunku ruchu postępowego (rys.2). W tym drugim przypadku za powstanie siły nośnej odpowiedzialny jest efekt Magnusa, który tłumaczy m. in. zmiany trajektorii ruchu obracającej się piłki. (W przypadku przedstawionym na rys.2 piłka spadnie bliżej niż w przypadku gdyby się nie obracała. Stanie się tak, ponieważ oprócz siły grawitacji na piłkę będzie działała pionowo w dół siła nośna. Pojawi się ona w efekcie nierównomiernego podziału strug opływających piłkę (więcej przepłynie pod piłką niż nad). Wynika to nie z kształtu piłki (jest symetryczny wzgl. kierunku ruchu powietrza), lecz z faktu, iż obracająca się piłka pociąga za sobą strugi powietrza ze względu na ich lepkość (doskonale gładka powierzchnia piłki wykluczyłaby ten efekt). Gdyby piłka kręciła się w drugą stronę, zasięg rzutu uległby zwiększeniu, ponieważ siła nośna działałaby pionowo do góry, a więc przeciw sile grawitacji.)

15. Siła oporu ośrodka :

1. dla przepływów turbulentnych - wzór obowiązuje również dla dużych prędkości

[N] F_o - siła oporu ośrodka

c - współczynnik kształtu

S - powierzchnia natarcia (- rzutu na powierzchnię prostopa-
dłą do kierunku ruchu)

d_pl - gęstość ośrodka (płynu, w którym porusza się ciało)
v - prędkość ciała wzgl. ośrodka (np. jeśli biegniemy pod
wiatr będzie ona równa sumie prędkości człowieka wzgl.
Ziemi i prędkości wiatru)

1. Prawo Stokesa - przy przepływie laminarnym opór ośrodka jest proporcjonalny do prędkości v
   
   
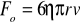
   zależność ta jest prawdziwa tylko dla bardzo małych prędkości v

2. lepkość:
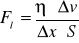
   η-współczynnik lepkości - zależy od rodzaju substancji, jej temperatury, ciśnienia

16. Liczba Reynoldsa - wielkość charakteryzująca przepływ - informuje czy jest on laminarny, czy nie; im większa tym większe wiry wokół ciała, względem którego jest przepływ.

, gdzie l - wymiar charakteryzujący ciało poruszające się w płynie
(=względem którego jest przepływ; np. rozpiętość skrzydeł)

v - prędkość lotu

 - współczynnik lepkości kinematycznej ośrodka;
między współczynnikiem  i ηzachodzi zależność:   η/d ,
gdzie d - gęstość ośrodka

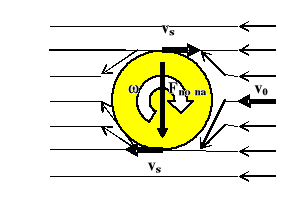
Rys. 2 Piłka „podkręcana”:   prędkość w ruchu obrotowym; v_s - prędkość mas powietrza „ciągniętych” przez piłkę (stycznych do jej powierzchni); v₀ - bezwzględna prędkość przepływu płynu; prędkość przepływu płynu bezpośrednio nad piłką: v_n=v₀-v_s; prędkość przepływu płynu bezpośrednio pod piłką: v_p=v₀+v_s. Prędkości spełniają więc warunek: v_n< v_p

Rys. 2

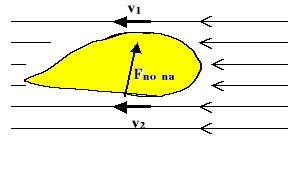
Rys. 1 Między prędkościami zachodzi zależność v₁>v₂

---