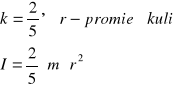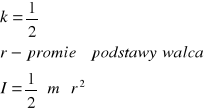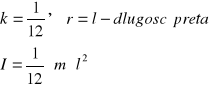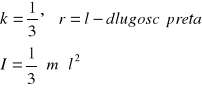WIADOMOŚCI OGÓLNE

Wszystkie wielkości fizyczne dzielimy na wielkości skalarne i wektorowe (w skrócie: skalary i wektory). Wielkości skalarne posiadają tylko wartość, np.: czas, długość, masa, energia, moc, temperatura i in.

Wielkości wektorowe są określane przez 4 cechy:

1. kierunek (czyli prosta, wzdłuż której działa wektor)

2. zwrot (określa, w którą stronę działa wektor)

3. punkt przyłożenia zw. też punktem zaczepienia (określa początek wektora)

4. wartość (informuje o długości wektora).

Z powyższego faktu wynika, że zmianę wektora powoduje zmiana którejkolwiek jego cechy (np. zmiana kierunku) podczas gdy zmiana wielkości skalarnej jest równoznaczna ze zmianą wartości

Wielkościami wektorowymi są np. przemieszczenie, prędkość, przyspieszenie, siła i in.

Elementy rachunku wektorowego:

(pogrubiona litera oznacza wektor, ta sama litera “zwykłej grubości - długość danego wektora)

Dodawanie wektorów - graficznie: a b

a

1. 
   
   
   reguła równoległoboku:

b

2. 
   
   reguła trójkąta:

a b

(a+b)

Wektor wypadkowy - wektor, będący sumą wektorową wektorów składowych; jego współrzędne otrzymuje się poprzez dodanie współrzędnych wektorów składowych (- “x_a” do “x_b”, “y_a” do “y_b” itd.) .

Jeśli wektory działają wzdłuż tej samej prostej (=mają ten sam kierunek), to wektor wypadkowy jest:

a) sumą składowych, jeśli ich zwroty były zgodne; a b

(a+b)

2. różnicą składowych, jeśli ich zwroty były przeciwne; a b

a (b-a)

Mnożenie wektorów:

1. iloczyn skalarny - wynikiem jest wielkość skalarna (czyli liczba) będąca polem równoległoboku wyznaczonego przez wektory; wartość wylicza się ze wzoru: a ° b = a⋅b⋅cosα, gdzie α- kąt zawarty między wektorami a i b

2. iloczyn wektorowy - wynikiem jest wektor prostopadły do mnożonych wektorów, którego zwrot wyznacza się przy użyciu reguły śruby prawoskrętnej, a długość (wartość iloczynu) wylicza się ze wzoru: a x b = a⋅b⋅sinα, gdzie α- kąt zawarty między wektorami a i b

Wszystkie wielkości fizyczne wyraża się w jednostkach układu SI. Oznacza to, że jeśli jakaś wielkość jest podana w jednostkach spoza tego układu, to trzeba ją przeliczyć; np. w ukł. SI jednostką mocy jest wat (1W), a nie koń mechaniczny (1KM), jeśli więc wartość mocy została podana w KM, to należy ją przeliczyć na waty wg zależności 1KM= 745,7W

Jeżeli dane są w pod- lub nadjednostkach, np. 3mm³, 8kJ, 0,2 kW/cm², to trzeba je również przeliczyć na jednostki podstawowe, czyli w przykładzie odpowiednio:

3 mm³ = 3⋅(0,001m)³ = 3⋅10^-9 m³ = 0,000000003m³

8 MJ = 8⋅10⁶ J = 8 000 000 J

0,2 kW/cm² = 0,2⋅1000W/(0,01m)² =0,2⋅1000W/10^-4 m² = 0,2⋅10⁷ W/m² = 2 000 000 W/m²

RUCH CIAŁ I JEGO OPIS

Ruchem nazywamy zmianę położenia ciała w czasie.

Ciało (układ ciał), względem którego opisujemy położenie innych ciał, nazywamy układem odniesienia.

Położenie ciała (s) -wektor określający przemieszczenie ciała względem początku układu odniesienia. Przemieszczenie (Δs) - wektor, będący efektem zmiany położenia, co do wartości równy różnicy wektorów położenia końcowego i początkowego.

Nie ma bezwzględnego ruchu i bezwzględnego spoczynku - każdy ruch (spoczynek) jest względny. Ta cecha ruchu oznacza, że ciało może być w ruchu względem jednego układu odniesienia i równocześnie pozostawać w spoczynku względem innego układu.

Tor ruchu punktu materialnego to linia, którą zakreśla punkt w czasie ruchu (czyli krzywa, po której porusza się ten punkt w układzie odniesienia).

Długość toru, przebytego przez punkt w czasie ruchu, nazywamy drogą. Droga jest wielkością skalarną.

Prędkość (v) - wektor; jest to stosunek zmiany położenia (=przemieszczenia - Δs) do czasu, w którym ta zmiana nastąpiła (- Δt)

, Δs = s_k - s_p s_k - położenie końcowe, s_p - położenie początkowe

Δt = t_k - t_p t_k - czas końcowy, t_p - czas początkowy

Jest wektorem, którego kierunek i zwrot jest zgodny z wektorem przemieszczenia.

• Prędkość średnia jest to stosunek całkowitego przemieszczenia ciała do czasu, w którym ono nastąpiło.

• Prędkość chwilowa jest to prędkość wyznaczona dla bardzo krótkiego czasu (Δt dążącego do 0)

Ruch jednostajny - charakteryzuje się stałą prędkością, a więc jego prędkość chwilowa jest równa prędkości średniej.

Wzory:

przemieszczenie :

prędkość :

Wykresy:

s v

„do przodu”

“do przodu”

spoczynek

0

0

t “do tyłu” t

„do tyłu”

koniec opisu ruchu jednostajnego

Przyspieszenie (a) - wektor; jest to przyrost prędkości do czasu, w którym ten przyrost nastąpił.

, Δv = v_k - v_p v_k - prędkość końcowa, v_p - prędkość początkowa

Δt = t_k - t_p t_k - czas końcowy, t_p - czas początkowy

• Przyspieszenie średnie jest to stosunek całkowitego przyrostu prędkości ciała do czasu, w którym ten przyrost nastąpił.

• Przyspieszenie chwilowe jest to przyspieszenie wyznaczone dla bardzo krótkiego czasu (Δt dążącego do 0)

Ruch zmienny - przyspieszenie jest różne od zera; jeśli jest dodatnie, to ruch jest przyspieszony, a jeśli ujemne - ruch opóźniony. Jeśli przyspieszenie jest dodatkowo stałe (=niezmienne w czasie), to ruch jest jednostajnie zmienny

Wzory:

przemieszczenie :

prędkość :

Wykresy:

s r.j.przysp. v a

r.j.przysp. r.j.przysp.

r.j.opóźn

0

. t

s₀ r.j.opóźn. r.j.opóźn.

t t

DYNAMIKA

I zasada dynamiki

Jeśli na ciało (lub układ ciał) nie działa żadna siła lub działające siły równoważą się, to ciało to pozostaje w spoczynku lub porusza się ruchem jednostajnym postępowym.

Ciało pozostaje w spoczynku jeśli w momencie zrównoważenia się sił jego prędkość była równa 0, natomiast porusza się ruchem jednostajnym jeśli prędkość miała wartość różną od 0.

II zasada dynamiki

Jeśli na ciało (lub układ ciał) o masie m działa stała niezrównoważona siła F, to ciało to porusza się ruchem jednostajnie zmiennym z przyspieszeniem a wprost proporcjonalnym do siły wypadkowej (F), a odwrotnie proporcjonalnym do jego masy (m)

III zasada dynamiki

Jeżeli na ciało A działa ciało B z siłą F_BA, to ciało A działa na ciało B z taką samą co do wartości i kierunku siłą , ale o przeciwnym zwrocie i innym (!) punkcie przyłożenia. (akcja = reakcja)

F_BA = -F_AB

(np. F_BA -siła grawitacji , F_AB - siła sprężystości podłoża)

Pęd jest to iloczyn prędkości (v) i masy danego ciała (m). p = m⋅v [kg⋅m/s = N⋅s]

Popęd siły (-“impuls siły”) jest to iloczyn siły (F) przez czas jej działania (Δt). π = F⋅Δt [N⋅s]

Jeżeli porównamy oba w/w wzory na przyspieszenie (a)

i przekształcimy je,

to otrzymamy inną postać II zasady dynamiki (-bardziej ogólną), która brzmi:

Przyrost pędu jest równy popędowi siły.

Z powyższych przekształceń wynika również wzór na siłę:
, co interpretujemy następująco: siła jest wielkością charakteryzującą tempo zmiany pędu (im większa siła, tym większe tempo zmian czyli tym szybciej zmienia się pęd)

Zasada zachowania pędu

Jeżeli na ciało (lub układ ciał) nie działają siły zewnętrzne lub działające siły równoważą się, to jego pęd jest zachowany (p = const.).

Innymi słowy: suma pędów ciał wchodzących w skład układu jest przed i po zdarzeniu stała, jeśli F_zew = 0

p_{układu przed zdarzeniem} = p_{układu po zdarzeniu}= const.

(Przez zdarzenie rozumie się np. rozpad ciała na części bez udziału sił zewnętrznych lub zderzenie ciał wchodzących w skład układu)

Uwaga: siły zewnętrzne to te spoza układu np. siły oporu, dla odróżnienia od sił wewnętrznych, czyli „wyzwolonych” w układzie np. sił oddziaływań między ciałami (-grawitacyjnych, elektrostatycznych i in.)

Zasada ta jest m.in. spełniona w zderzeniach sprężystych i niesprężystych.

Energia mechaniczna jest to suma energii kinetycznej i potencjalnej danego ciała (układu ciał)

E_m = E_k + E_p

• Energia kinetyczna zależy od prędkości jaką posiada ciało (v) - zależność ta wyraża się wzorem:

, gdzie m - masa ciała

• Energia potencjalna zależy od położenia ciała względem poziomu odniesienia (h) (= wysokości, na jakiej się ciało znajduje) - zależność ta wyraża się wzorem:

, gdzie m - masa ciała,

g - przyspieszenie ziemskie

Zasada zachowania energii mechanicznej

Jeżeli na ciało (lub układ ciał) nie działają siły rozpraszające energię (np. siły oporu), to jego energia mechaniczna jest zachowana (E_m = const.).

Z zasady tej wynika, że jeśli jest spełniony warunek (F_rozprasz = 0), to suma E_k i E_p jest wielkością stałą, natomiast możliwe jest zwiększanie jednej z energii kosztem drugiej.

Zasada ta jest m.in. spełniona w swobodnym spadku, rzutach i zderzeniach sprężystych

Praca jest to iloczyn skalarny wektora przesunięcia s przez wektor siły F. Wyraża się wzorem:

, gdzie α - kąt zawarty między wektorami s i F

• Ze względu na wartość tego kąta praca może być dodatnia, ujemna lub równa 0.

• Praca jest równoważna energii, a więc jest równa przyrostowi energii mechanicznej. W szczególności praca polegająca na zmianie prędkości (v) bez zmian położenia w pionie (bez zmian h) jest równa przyrostowi energii kinetycznej, a praca związana tylko ze zmianą położenia względem poziomu odniesienia (h) bez zmian prędkości (v) jest równa przyrostowi energii potencjalnej.

Moc jest to stosunek pracy (W) do czasu (t), w którym została ona wykonana, względnie - jest to stosunek energii (E) do czasu (t), w którym została ona wydatkowana lub wyzwolona.

.

Moc jest więc miarą szybkości wykonywania pracy i/lub tempa przemian energetycznych (nawet, gdy żadna praca nie jest wykonywana)

• Inny wzór (wynikający z definicji: mocy, pracy i prędkości średniej):
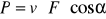
  , gdzie α - kąt zawarty między wektorami v i F
  Wzór ten można zinterpretować następująco (upraszczając procesy zachodzące w człowieku): człowiek, dysponując ściśle określoną mocą, może wykonywać albo ruchy szybkie, ale z niewielką siłą (np. ćwiczenia refleksu, szybkości reakcji)), albo wyzwalać dużą siłę, ale przy małej prędkości ruchu (np. ćwiczenia siłowe), albo też wykonywać ruchy charakteryzujące się wartościami pośrednimi F i v (np. ćwiczenia ogólnorozwojowe)

MECHANIKA BRYŁY SZTYWNEJ

Bryła sztywna - (def.) model ciała rzeczywistego charakteryzujący się tym, że nie odkształca się pod wpływem sił (inaczej można powiedzieć, że odległości pomiędzy punktami materialnymi, z których składa się bryła, nie ulegają zmianie).

Środek masy - punkt niematerialny (czyli taki, który może znajdować się poza ciałem np. u człowieka podczas wykonywania „mostka”) będący geometrycznym środkiem ciała; można go wykorzystywać, gdy przedstawia się ruch bryły jako ruch punktu materialnego.

Środek ciężkości - punkt niematerialny (jak wyżej), w którym jest przyłożona siła ciężkości ciała

(Sposoby znajdowania tych punktów były m.in. przedmiotem ćwiczeń. Korzysta się z warunku równoważenia się momentów składowych sił ciężkości z wypadkową siłą - zastępującą działanie wszystkich składowych. W układzie współrzędnych otrzymany z tego warunku wzór na współrzędne środka ciężkości względnie środka masy przyjmie postać:

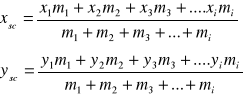
gdzie: x₁, x₂, y₃, x_i, y₁, y₂, y₃, y_i -
współrzędne punktów materialnych
wchodzących w skład ciała (układu
ciał);

i - ilość punktów wchodzących w skład ciała (układu ciał);

x_sc, y_sc - współrzędne środka masy (środka ciężkości) ciała
(układu ciał);

m₁, m₂, m₃, m_i - masy punktów materialnych wchodzących
w skład ciała (układu ciał) (dla środka ciężkości zamiast
mas wstawia się ciężary poszczególnych punktów: Q₁,
Q₂, Q₃, Q_i, (Q = mg, g - przyspieszenie ziemskie);
prowadzi to jednak do takiego samego wzoru, ponieważ
g wystąpi i w liczniku i w mianowniku we wszystkich
wyrażeniach, a więc uprości się)

Przykład zastosowania powyższych zależności -patrz zad.6 z listy 2 dla WF

W przypadku, gdy ciało /układ ciał nie znajduje się w układzie współrzędnych, do wyznaczenia położenia środka masy/ciężkości wykorzystuje się warunek równoważenia się momentów sił oraz jakąś zależność określającą położenie punktów materialnych wchodzących w skład ciała (układu ciał) - patrz zad.4 z listy 2 dla WF

Parametry kinematyczne
(analogie między ruchami)

Związek między miarami kąta: 180° = π rad , czyli 1rad ≈ 57°

ruch postępowy		ruch obrotowy
Przemieszczenie - Δs [m]		Przemieszczenie kątowe - Δα [rad]
Prędkość - v [m/s]		Prędkość kątowa - ω [rad/s]
Przyspieszenie - a [m/s^2]		Przyspieszenie kątowe - ε [rad/s^2]

parametr liniowy = r ⋅ parametr kątowy, gdzie r - promień wodzący (promień krzywizny); np.: v = r⋅ ω

Z powyższej tabelki można skorzystać w następujący sposób:

Jeśli znam jakąś zależność w ruchu postępowym, to mogę ją wykorzystując odpowiedniki w tabelce, przetransponować na zależność dla ruchu obrotowego np.:

Wzór definicyjny na prędkości v w ruchu postępowym miał postać:

Z tabelki wiem, że prędkości v [m/s] odpowiada w ruchu obrotowym prędkość kątowa  [rad/s], przemieszczeniu s[m] odpowiada przemieszczenie kątowe  [rad], natomiast czas w obu ruchach płynie tak samo, a więc wzór definicyjny na prędkość kątową przyjmie postać:

Analogicznie można otrzymać wszystkie inne wzory (na przemieszczenie, prędkość czy przyspieszenie w ruchu obrotowym jednostajnym i/lub zmiennym a także wzory „dynamiczne” - uwzględniając tabelkę poniżej- na energię kinetyczną ciała obracającego się, przyspieszenie kątowe z II zasady dynamiki, moment pędu i in); np:
ze wzoru

[J] (energia kinetyczna ciała w ruchu postępowym)

otrzyma się w ten sposób wzór:

[J] (energia kinetyczna ciała w ruchu obrotowym)

Nowe parametry (charakterystyczne dla ruchu po okręgu):

Częstotliwość (f) - (def.) ilość cykli (obiegów, obrotów) w jednostce czasu; wielkość skalarna, jednostka herc [1Hz].

Okres (T) - (def.) czas trwania jednego cyklu (obiegu, obrotu); wielkość skalarna, jednostka sekunda [1s]

Wielkości te są powiązane ze sobą następującą zależnością:

Uwzględniając te parametry otrzymujemy zależność np. na prędkość kątową (szczególny przypadek - dla pełnego obrotu):

Parametry dynamiczne

ruch postępowy		ruch obrotowy
Masa - m [kg]		Moment bezwładności - I [kgm^2]
Siła - F [N]		Moment siły - M [Nm]
Pęd - p [kgm/s = Ns]		Moment pędu - L [kgm^2/s = Nsm]

Dlaczego potrzebne są nowe parametry?

• Miara bezwładności:

• masa w ruchu postępowym




• bezwładność w ruchu obrotowym zależy nie tylko od masy, ale również od rozmieszczenia tej masy względem osi obrotu - moment bezwładności jest parametrem uwzględniającym ten fakt.

• Efekt działania siły zależy od jej wartości, kierunku działania, zwrotu i punktu przyłożenia;

• siła przyłożona do środka masy bryły lub działająca wzdłuż prostej przechodzącej przez środek masy wywoła wyłącznie zmiany w ruchu postępowym (sprawi, że taki ruch wystąpi, zmieni jego parametry lub zatrzyma ciało poruszające się takim ruchem)

• pojedyncza siła działająca wzdłuż prostej, która nie przechodzi przez środek masy bryły wywoła zmiany w ruchu postępowym i obrotowym

⇓

Moment siły względem pewnego punktu (np. dla bryły swobodnej, nieograniczonej w żaden sposób jest to środek masy) uwzględnia wartość siły, jej zwrot a także odległość kierunku jej działania od tego punktu, a więc pozwala przewidzieć skutki działania siły na bryłę.

Moment bezwładności - (def.) suma iloczynów mas punktowych (Δm_i) przez kwadrat ich odległości od osi obrotu (r_i)

(zapis ten oznacza, że bryłę podzielono na n części o wymiarach punktu i masie Δm_i, r_i oznacza odległość punktu i od osi obrotu; dla każdego z tych punktów wyliczono moment bezwładności, a następnie zsumowano je otrzymując w ten sposób moment bezwładności całej bryły ⇒ moment bezwładności układu jest równy sumie momentów bezwładności części składowych tego układu liczonych wzgl. tej samej (!) osi obrotu)

Inny wzór (uwzględniający powyższą operację matematyczną):

, gdzie k - współczynnik kształtu bryły, m - jej masa,

r - jakiś charakterystyczny dla bryły wymiar (np. wysokość dla pręta, promień podstawy dla walca itp.), informuje o rozmieszczeniu masy w bryle

np.

dla kuli wzgl. osi przechodzącej przez jej środek:	dla walca wzgl. osi prostopadłej do podstawy, przechodzącej przez jej środek:
dla pręta wzgl. osi do niego prostopadłej, przechodzącej przez jego środek:	dla pręta wzgl. osi do niego prostopadłej, przechodzącej przez jego koniec:

Centralny moment bezwładności - (def.) moment bezwładności wyznaczony względem osi obrotu przechodzącej przez środek masy bryły. Bryła może mieć nieskończenie wiele takich momentów, ponieważ przez punkt (tu: =środek masy) można przeprowadzić nieskończenie wiele prostych (tu: =osi obrotu)

Twierdzenie Steinera

• Dotyczy osi równoległych; pozwala obliczyć moment bezwładności bryły (o masie m) wzgl. nowej osi (I_d), jeśli znamy moment bezwładności wzgl. innej osi, równoległej do nowej (I_o) oraz odległość osi od siebie (d).

Uwaga: Oś „stara” jest zawsze osią centralną, czyli przechodzącą przez środek masy (!)

Moment siły - (def.1)

• Iloczyn wektorowy wektora promienia wodzącego (r) przez wektor siły (F)

• gdzie promień wodzący jest to odległość od osi obrotu do punktu przyłożenia siły

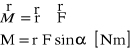
gdzie α - kąt zawarty między wektorami r i F

Moment siły - (def.2)

• Iloczyn wektorowy wektora ramienia siły (R) przez wektor siły (F)

• gdzie ramię siły jest to odległość od osi obrotu do kierunku działania siły

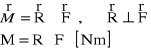
Promień wodzący i ramię siły dla dwóch przykładowych przypadków:

.

R F F

α α

r r

R

^.

Moment pędu jest to iloczyn wektorowy wektora promienia wodzącego (r) przez wektor pędu (p)

gdzie promień wodzący jest to odległość od osi obrotu do punktu zaczepienia wektora pędu

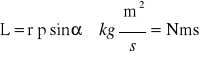
gdzie α - kąt zawarty między wektorami r i p

Inny wzór: L = I⋅ω, gdzie I - moment bezwładności, ω - prędkość kątowa

Zasada zachowania momentu pędu

Jeżeli na ciało (lub układ ciał) nie działają momenty sił zewnętrznych lub działające momenty sił równoważą się, to jego moment pędu jest zachowany (L = const.).

Jeśli np. jakiś układ porusza się ruchem obrotowym z prędkością ₁ i w efekcie działania sił wewnętrznych dojdzie do zmiany rozmieszczenia masy względem osi obrotu, a więc do zmiany momentu bezwładności układu (z I₁ na I₂), to zmieni się również jego prędkość obrotowa (=kątowa) na ₂; przy czym jeśli moment bezwładności wzrośnie, to prędkość zmaleje i odwrotnie (-jest to zależność odwrotnie proporcjonalna).

Prawo wykorzystuje się np. do wyjaśnienia zmian prędkości kątowej człowieka podczas kręcenia piruetów czy też - prędkości kątowej nóg wzgl. stawu biodrowego podczas chodu/biegu.

Energia kinetyczna ciała toczącego się jest równa sumie energii kinetycznej tego ciała w ruchu postępowym E_kp i obrotowym E_ko

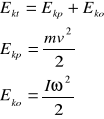
gdzie m - masa ciała,

v - prędkość w ruchu postępowym,

I -moment bezwładności,

 - prędkość kątowa (w ruchu obrotowym)

Równowaga mechaniczna - ciało znajduje się w równowadze mechanicznej, jeśli jest w spoczynku (a więc wypadkowa siła i wypadkowy moment siły działające na ciało są równe 0) i zajmuje minimalne możliwe w danym miejscu położenie. Położenie to jest charakteryzowane przez zachowanie się energii potencjalnej E_p tego ciała w najbliższym sąsiedztwie tego położenia - i tak:

E_p [J]

rys.1 d [m]

E_p [J]

rys.2 d [m]

E_p [J]

rys.3 d [m]

- jeśli E_p w miejscu, w którym znajduje się ciało jest maksymalna (w porównaniu z otoczeniem), to równowagę taką nazywamy równowagą chwiejną (rys.1); wytrącenie ciała z równowagi sprawia, że zmienia ono swoje położenie (d) tak, by możliwie najbardziej zmniejszyć swoją E_p; nie jest ono również zdolne do samodzielnego (bez udziału sił z zewnątrz) powrotu na uprzednio zajmowaną pozycję

- jeśli E_p w miejscu, w którym znajduje się ciało jest taka sama, jak w otoczeniu tego punktu, to równowagę taką nazywamy równowagą obojętną (rys.2); wytrącenie ciała z równowagi sprawia, że zmienia ono swoje położenie (d), ale nie zmienia E_p (-wszędzie dookoła E_p jest taka sama); nie jest ono również zdolne do samodzielnego (bez udziału sił z zewnątrz) powrotu na uprzednio zajmowaną pozycję

- jeśli E_p w miejscu, w którym znajduje się ciało jest minimalna (w porównaniu z otoczeniem), to równowagę taką nazywamy równowagą stałą (=trwałą) (rys.3); wytrącenie ciała z równowagi sprawia, że ciało przez chwilę wychyla się od położenia pierwotnego (=położenia równowagi) z coraz mniejszą amplitudą aż do zatrzymania; nie zmienia więc ani swojego położenia, ani E_p;

Równowaga mechaniczna ciała zależy od położenia środka ciężkości i od powierzchni podparcia (powierzchni zawartej między punktami styku z podłożem). Im wyżej znajduje się środek ciężkości ciała i im mniejsza jest powierzchnia podparcia, tym trudniej jest mu utrzymać równowagę.

(a-b)

oś obrotu

(przechodząca przez punkt wskazany strzałką, ale nie leżąca w płaszczyźnie rysunku, lecz do niej prostopadła)

(a+b)

---