Imię i nazwisko: Łukasz Loose
IMiF, Fizyka Techniczna
Rok I, semestr II
Grupa A
Laboratorium Fizyki
Ćwiczenie nr 6
Wyznaczanie momentów bezwładności bryły za pomocą wahadła torsyjnego.
Definicje.
Bryła sztywna - to takie ciało, w którym pod wpływem działających
sił zewnętrznych nie zmienia się wzajemna odległość pomiędzy cząsteczkami tego ciała (siły te nie zmieniają kształtu ciała). Z definicji wynika, że dane ciało czasami możemy traktować jako bryłę sztywną (wtedy, gdy działające siły są zbyt małe aby to ciało odkształcić), a innym razem, gdy działające siły są większe, ciało przestaje być bryłą sztywną.
Momentem bezwładności I bryły względem danej osi nazywamy
sumę iloczynów mas poszczególnych punktów bryły i kwadratów ich odległości od danej osi, a więc:
![]()
Aby znaleźć moment bezwładności ciała należy „podzielić” to ciało na fragmenty tak małe, aby każdy z nich można było traktować jak punkt materialny o pewnej masie mi, pomnożyć jego masę przez kwadrat jej odległości ri2 od osi obrotu i wszystkie otrzymane iloczyny do siebie dodać. W praktyce, do ciał rzeczywistych, a więc takich dla których masa jest rozłożona w sposób ciągły stosuje się postać całkową definicji, pozwalającą obliczać rzeczywiste momenty bezwładności:
![]()
We wzorze tym r2 oznacza zmienną określającą odległość elementu masy dm od osi obrotu.
Przykładowe monety bezwładności brył:
Dla kuli
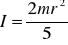
Dla walca
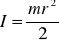
Dla pręta
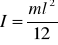
Wszystkie powyższe wzory określają momenty bezwładności brył względem osi przechodzących przez środek masy danej bryły.
Twierdzenie Steinera - mówi, że jeśli znamy moment bezwładności
I0 danego ciała względem osi przechodzącej przez środek masy tego ciała, to aby obliczyć moment bezwładności I względem dowolnej innej osi równoległej do niej, należy do momentu I0 dodać iloczyn masy ciała i kwadratu odległości między tymi osiami, czyli md2 :
![]()
Wahadło torsyjne jest to ciało sztywne zawieszone na pionowym
nieważkim pręcie lub nici(sprężystych), którego górny koniec jest umocowany nieruchomo, a oś Oz pokrywa się z jedną ze swobodnych osi ciała.
Drgania torsyjne wywołane są siłami sprężystości powstającymi w pręcie po jego skręceniu wokół osi Oz. Okres tych drgań jest równy:
![]()
gdzie
I - moment bezwładności
D - sztywność skręcania pręta(moment kierujący)
Przebieg doświadczenia.
Aby znaleźć moment bezwładności I danej bryły, należy umieścić ją na wahadle torsyjnym i zmierzyć jego okres drgań T. Następnie należy wykorzystać bryłę o znanym momencie bezwładności I0, zmierzyć okres drgań wahadła z tą bryłą i zapisać następujące równania:
![]()
- okres drgań ramki z walcem
![]()
- okres drgań ramki z bryłą
![]()
- okres drgań ramki bez obciążenia
Wyprowadzenie wzoru roboczego.
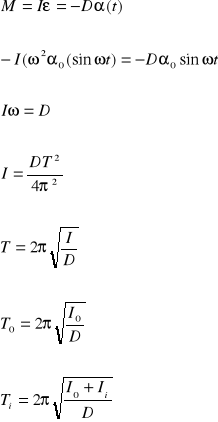
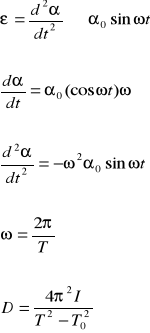
Po podniesieniu stronami do kwadratu dwóch ostatnich równań i odjęciu ich stronami, otrzymuję:
![]()
Ostatecznie:
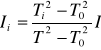
gdzie:
Ti - okres drgań ramki z bryłą
T0 - okres drgań ramki bez obciążenia
T - okres drgań ramki z walcem
I - moment bezwładności walca
Teoretyczne momenty bezwładności.
Dla walca:
h
r
h = 0,05m
r = 0,0245m
![]()
![]()
![]()
![]()
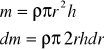
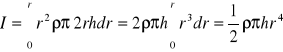
![]()
Obliczam niepewność pomiaru momentu bezwładności walca.
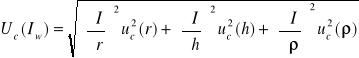
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Niepewność rozszerzona:
![]()
dla α=0,95 i kα=2
Ostatecznie niepewność momentu bezwładności walca w raz z niepewnością wynoszą:
![]()
Dla prostopadłościanu:
b
a
c
a=0,04m
b=0,06m
c=0,1m
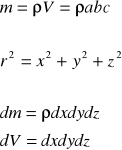
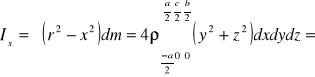
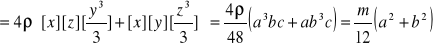
![]()
![]()
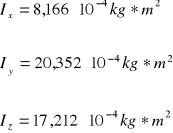
Obliczenia.
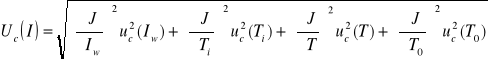
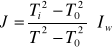
[kg*m2]
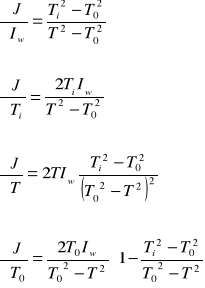
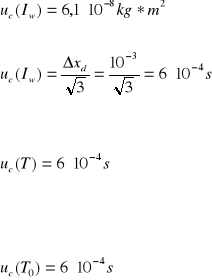
Niepewność pomiaru dla osi X wynosi:
![]()
dla α=0,95 i kα=2
Niepewność pomiaru dla osi Y wynosi:
![]()
dla α=0,95 i kα=2
Niepewność pomiaru dla osi Z wynosi:
![]()
dla α=0,95 i kα=2
Momenty bezwładności prostopadłościanu wynoszą:
Dla osi X
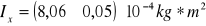
Dla osi Y
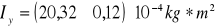
Dla osi Z
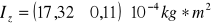
Wszystkie obliczenia zostały wykonane dla prawdopodobieństwa α=0,95 oraz współczynnika prawdopodobieństwa kα=2.
Wnioski.
Wyniki otrzymane podczas przeprowadzania doświadczenia, pokrywają się z wynikami otrzymanymi przez teoretyczne obliczenia momentów bezwładności prostopadłościanu względem poszczególnych osi.
Otrzymane odstępstwa w małej mierze są spowodowane pomiarem czasu. Głównym ich powodem jest fakt, iż badany prostopadłościan nie był idealny, ponieważ miał podszlifowane narożniki co w głównej mierze wpłynęło na różnicę w wynikach teoretycznych i tych przeprowadzonych w laboratorium.
8
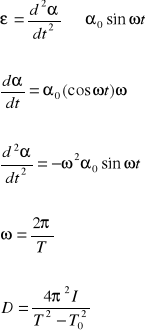
Wyszukiwarka
Podobne podstrony:
cw26(teoria), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
RLC(szacowanie)-24, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fiz
cw31(teoria), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
cw21(teoria), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
modu- younga, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
predkosc dzwieku, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyk
cw31 - wykres (aproksymacja prosta), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizy
fiza24, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka Labolato
fala dzwiekowa, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka
wahadlo maxwella, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyk
65 tabele, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka Labol
modu- younga - opracowanie, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - labo
cw43(teoria), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka La
Wyznaczanie ciep-a topnienia lodu(czewrwony), Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - labo
wsp pow extra, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka L
fiz.43, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka Labolato
teory cw.2b, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki, Fizyka Lab
więcej podobnych podstron