Niech
będzie daną funkcją i niech
będzie punktem skupienia zbioru
( punkt
nazywamy punktem skupienia zbioru
, jeżeli w każdym otoczeniu tego punktu znajdują się punkty zbioru
różne od
, tzn.

:

) .

Definicja 1 . Mówimy , że liczba
jest granicą funkcji
w punkcie
, co symbolicznie zapisujemy

jako
, jeżeli spełniony jest jeden z dwóch równoważnych warunków :

( C )


:
;

( H )
\
:


.

Twierdzenie 1 . Jeżeli funkcje
i
mają w punkcie
granice ( właściwe ) , to

1)
,

2)
,

3)
dla dowolnego
,

4)
,

5)
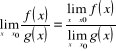
, o ile
,

6)
.

( W ostatnim wzorze zakładamy , że wyrażenia po obu stronach równości mają sens . )

Przykłady .

1)
,

2)
=
,

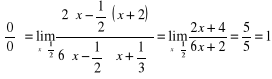
3)

4)
,

5)
,

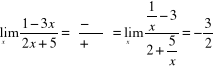
6)
,

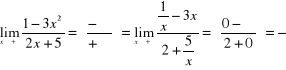
7)
,

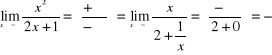
8)
,

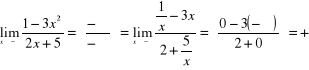
9)
,

Twierdzenie 2 . Jeżeli funkcje
określone na zbiorze
spełniają warunki

(a)
dla każdego
z pewnego sąsiedztwa punktu
,

(b)
,

to wtedy granica
istnieje i
.

Przykład . Obliczyć
.

Mamy
. Ponieważ
, to
, skąd wynika , że i
.

Twierdzenie 3 . ( O pewnych szczególnych granicach )

(a)
, (b)
.

Przykłady

1)
,

2)
,

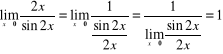
3)
,

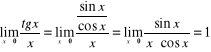
4)
,

5)
.

6)
,

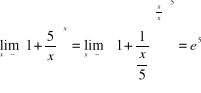
7)
.

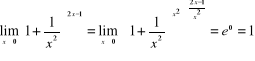
GRANICA FUNKCJI

3

---