Politechnika Lubelska w Lublinie |
|||
Laboratorium elektrotechniki |
Ćwiczenie nr: 8 |
||
Grzesiak Paweł Gotner Michał Bekiesza Krzysztof |
Semestr: III |
Grupa: ED. 3.4 |
Rok akadem.: 98/99 |
Temat: Stany nieustalone w obwodach z elementami RC |
Data wykonania: 16.12.98
|
Ocena:
|
|
Cel ćwiczenia:
Celem ćwiczenia jest zapoznanie się i praktyczne sprawdzenie stanu nieustalonego w obwodzie RC.
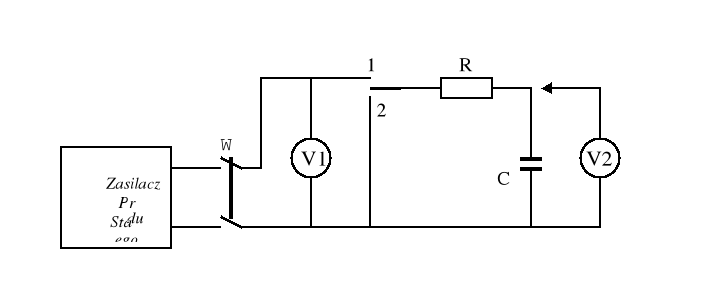
Schemat pomiarowy:

Dobór przyrządów:
V1 - Woltomierze LM - 3,
V2 -Digitalvolmeter V240 (o rezystancji RV =14 MΩ)
Zasilanie z tablicy 5V
1. Ładowanie kondensatora
C=18μF R1=1MΩ RV=14MΩ τ1 = 16,8s |
C=18μF R2=4MΩ RV=14MΩ τ2 =56 s |
||||||||
t |
U |
uc |
uR |
I |
t |
u |
uc |
uR |
i |
s |
V |
V |
V |
μA |
s |
V |
V |
V |
μA |
0 |
5 |
0 |
5 |
5 |
0 |
5 |
0 |
5 |
1,250 |
30 |
|
3,3 |
1,7 |
1,464 |
30 |
|
1,25 |
3,75 |
0,848 |
60 |
|
4,11 |
0,89 |
0,596 |
60 |
|
1,99 |
3,01 |
0,610 |
90 |
|
4,31 |
0,69 |
0,382 |
90 |
|
2,5 |
2,5 |
0,446 |
120 |
|
4,37 |
0,63 |
0,318 |
120 |
|
2,81 |
2,19 |
0,347 |
150 |
|
4,4 |
0,6 |
0,286 |
150 |
|
3,02 |
1,98 |
0,279 |
180 |
|
4,41 |
0,59 |
0,275 |
180 |
|
3,16 |
1,84 |
0,234 |
|
210 |
|
3,25 |
1,75 |
0,205 |
||||
|
240 |
|
3,32 |
1,68 |
0,183 |
||||
|
270 |
|
3,36 |
1,64 |
0,170 |
||||
|
300 |
|
3,39 |
1,61 |
0,160 |
||||
|
330 |
|
3,41 |
1,59 |
0,154 |
||||
Wzory i obliczenia
![]()
- teoretyczna stała czasowa
![]()
- teoretyczna stała czasowa
![]()
![]()
Charakterystyki uC = f(t), uR = f(t), i = f(t) dla C = 18μF i R1 = 1MΩ, RV=14MΩ
Charakterystyki uC = f(t), uR = f(t), i = f(t) dla C = 18μF i R2 = 4MΩ, RV=14MΩ
2. Rozładowanie kondensatora
C=18μF, RV=14MΩ, R1=1MΩ, τ1 = 16,8s |
C=18μF RV=14MΩ R2=4MΩ τ2 =56 s |
||||
t |
uc |
i |
t |
uc |
i |
s |
V |
μA |
s |
V |
μA |
0 |
4,41 |
-4,725 |
0 |
3,41 |
-1,096 |
18 |
1,8 |
-1,929 |
30 |
2,29 |
-0,736 |
36 |
0,85 |
-0,911 |
60 |
1,45 |
-0,466 |
54 |
0,45 |
-0,482 |
90 |
0,98 |
-0,315 |
72 |
0,24 |
-0,257 |
120 |
0,69 |
-0,222 |
90 |
0,15 |
-0,161 |
150 |
0,48 |
-0,154 |
108 |
0,1 |
-0,107 |
180 |
0,34 |
-0,109 |
126 |
0,065 |
-0,070 |
210 |
0,25 |
-0,080 |
144 |
0,05 |
-0,054 |
240 |
0,18 |
-0,058 |
162 |
0,039 |
-0,042 |
270 |
0,14 |
-0,045 |
|
330 |
0,086 |
-0,028 |
||
|
390 |
0,057 |
-0,018 |
||
Wzory i obliczenia
![]()
Charakterystyki uC = f(t), i = f(t) dla C = 18μF i R1 = 1MΩ, RV=14MΩ
Charakterystyki uC = f(t), i = f(t) dla C = 18μF i R2 = 4MΩ, RV=14MΩ
Wnioski
W ćwiczeniu woltomierz mierzący napięcie na kondensatorze był podłączony na stałe i jako element nie idealny posiada skończoną rezystancje (14MΩ), którą uwzględniłem w swoich obliczeniach. Zastosowałem metodę Tewenina aby obliczyć stałą czasową.
Stałe czasowe τ były wyznaczane jako czas, po którym napięcie na kondensatorze (podczas ładowania) osiągnęło 63,2% napięcia na kondensatorze w stanie ustalonym (4,41V i 3,41V), oraz przy badaniu rozładowania kondensatora jako 36,8% napięcia na kondensatorze w chwili t = 0s.. Jak widać stałe te mają wartości zbliżone do wartości teoretycznych obliczonych z wartości użytych elementów (RC).
Krzywe ładowania i rozładowania kondensatora otrzymane doświadczalnie zgadzają się z teoretycznymi przebiegami krzywej wykładniczej.
Czas ładowania jak i rozładowania zgodnie z teorią rośnie wraz ze wzrostem stałej czasowej τ (czyli wraz ze wzrostem wartości elementów R i C).
t [s]
uR, uC [V]
i [μA]
uC
i
uR
t [s]
uC
uR
i
uR, uC [V]
i [μA]
t [s]
t [s]
uC [V]
uC [V]
i [μA]
i [μA]
τ = 21s
τ = 59s
τ = 59s
τ = 20,05s
2,77
2,15
1,6
1,25