1. Odwzorowanie punktu, prostej i płaszczyzny w rzutach prostokątnych

1. Rzuty punktu

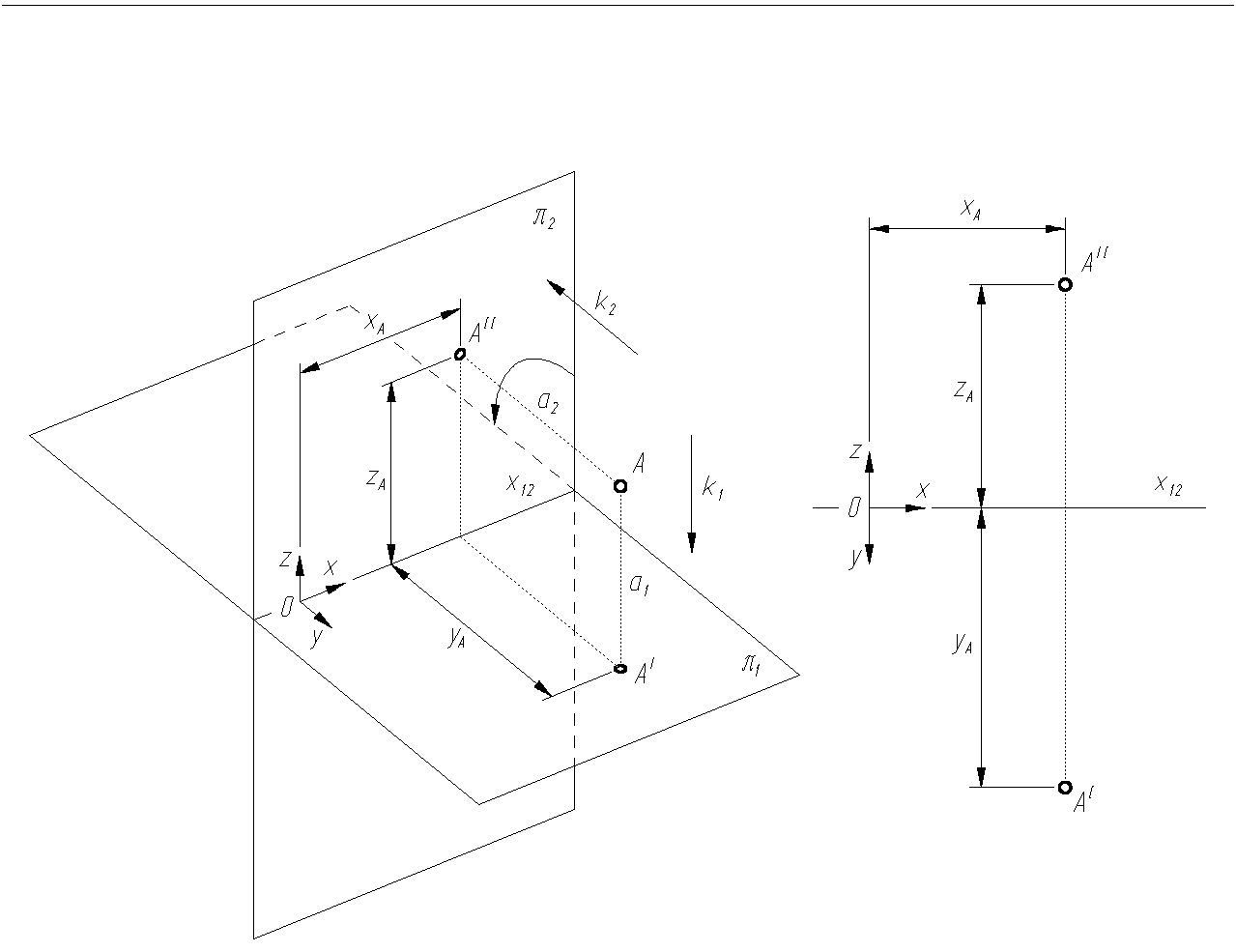
Dane są dwie prostopadłe do siebie rzutnie π₁ i π₂ i dwa kierunki rzutowania k₁ i k₂ prostopadłe odpowiednio do rzutni π₁ i π₂ (rys. 1.1). Rzutnię π₁ nazywamy rzutnią poziomą lub pierwszą, a rzutnię π₂ rzutnią pionową lub drugą. Krawędź przecięcia obu rzutni nazywamy osią rzutów i oznaczamy przez x₁₂.

Dowolny punkt A rzutujemy na obie rzutnie. Prosta rzutująca a₁, równoległa do kierunku rzutowania k₁, wyznacza na rzutni π₁ rzut poziomy punktu A, oznaczony jako A^I, natomiast prosta rzutująca a₂, równoległa do k₂, wyznacza na rzutni π₂ rzut pionowy punktu: A^II.

W celu uzyskania jednej płaszczyzny rysunku jedną z rzutni obracamy o kąt prosty dookoła osi rzutów tak, by zjednoczyła się z płaszczyzną drugiej rzutni. Otrzymujemy w ten sposób rozwinięty układ rzutni. W rozwiniętym układzie rzutni rzuty prostych rzutujących a₁ i a₂ na obie rzutnie tworzą jedną prostą prostopadłą do osi rzutów zwaną odnoszącą punktu. Punkty A^I i A^II w rozwiniętym układzie rzutni określają jednoznacznie położenie punktu A w przestrzeni.

Odległość punktu A od rzutni poziomej nazywamy wysokością punktu A. Może ona przyjmować znak + lub −, w zależności od tego czy punkt A leży powyżej lub poniżej rzutni π₁. Jednocześnie wysokość punktu równa się odległości z_A pionowego rzutu punktu (A^II) od osi rzutów ze znakiem + lub −, w zależności od tego czy rzut ten leży powyżej lub poniżej osi rzutów.

Odległość punktu A od rzutni pionowej nazywamy głębokością punktu A. Jest ona równa odległości y_A poziomego rzutu punktu (A^I) od osi rzutów i, podobnie jak wysokość, może przyjmować znak + lub − w zależności od położenia punktu A względem rzutni.

Odległość punktu A od płaszczyzny przechodzącej przez początek układu współrzędnych i prostopadłej do obu rzutni nazywamy szerokością punktu A. Szerokość jest ostatnią współrzędną (x_A) niezbędną do określenia położenia punktu w przestrzeni i może przyjmować znak + lub − w zależności od położenia początku układu współrzędnych (ustala się go w dowolnym punkcie leżącym na osi rzutów). We wszystkich przykładach omówionych w opracowaniu współrzędna x_A przyjmuje wartości dodatnie na prawo od początku układu współrzędnych.

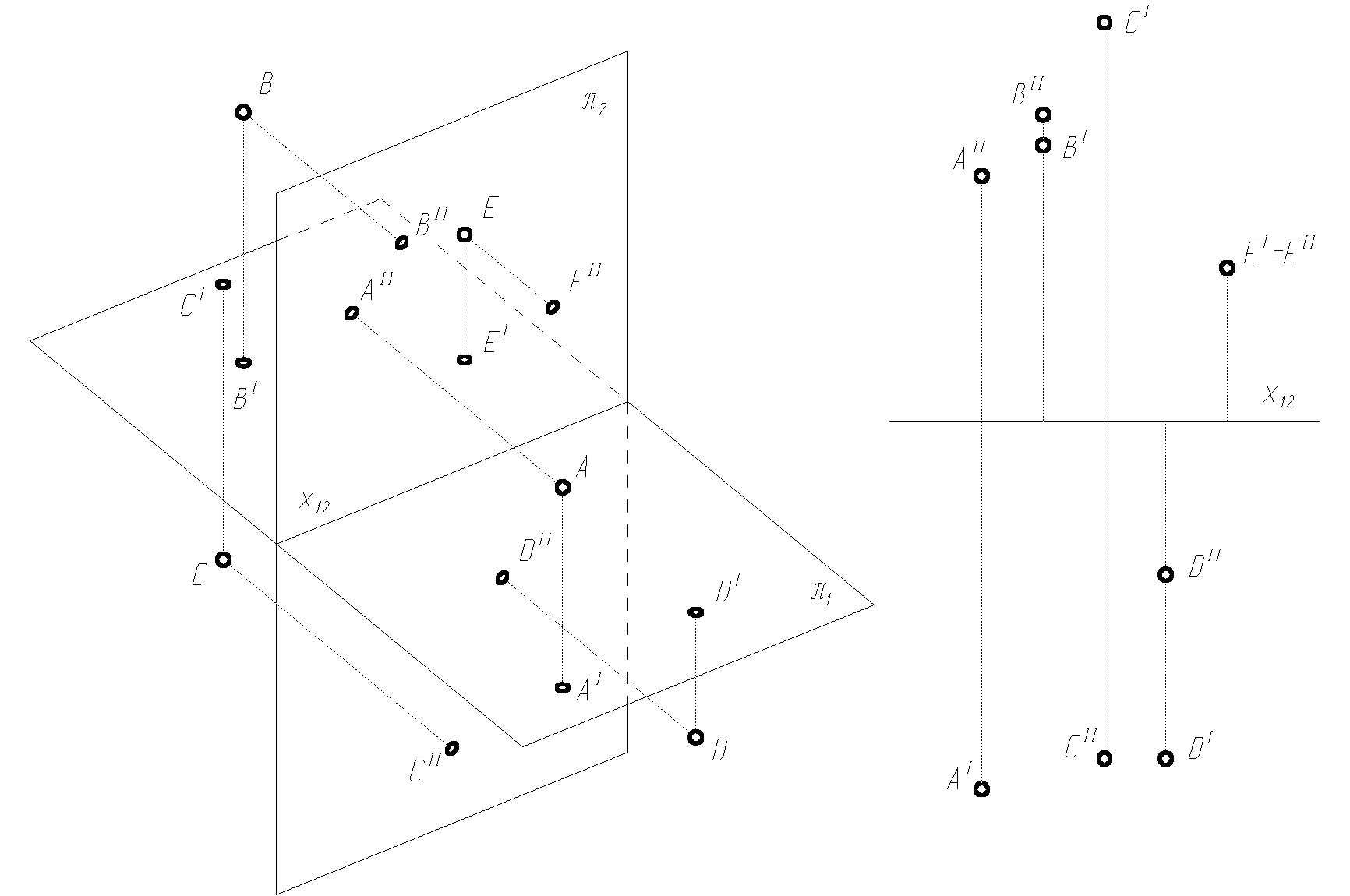
Na rysunku 1.2 pokazano punkty i ich rzuty dla różnych położeń punktów względem rzutni.

Rys. 1.1

Rys. 1.2

2. Rzuty prostej

Przez dwa różne punkty przechodzi jedna i tylko jedna prosta, w związku z tym położenie prostej w przestrzeni można określić za pomocą dwóch różnych jej punktów. Na rysunkach 1.3 i 1.4 pokazano rzuty prostych dla kilku różnych przypadków położenia prostej względem rzutni.

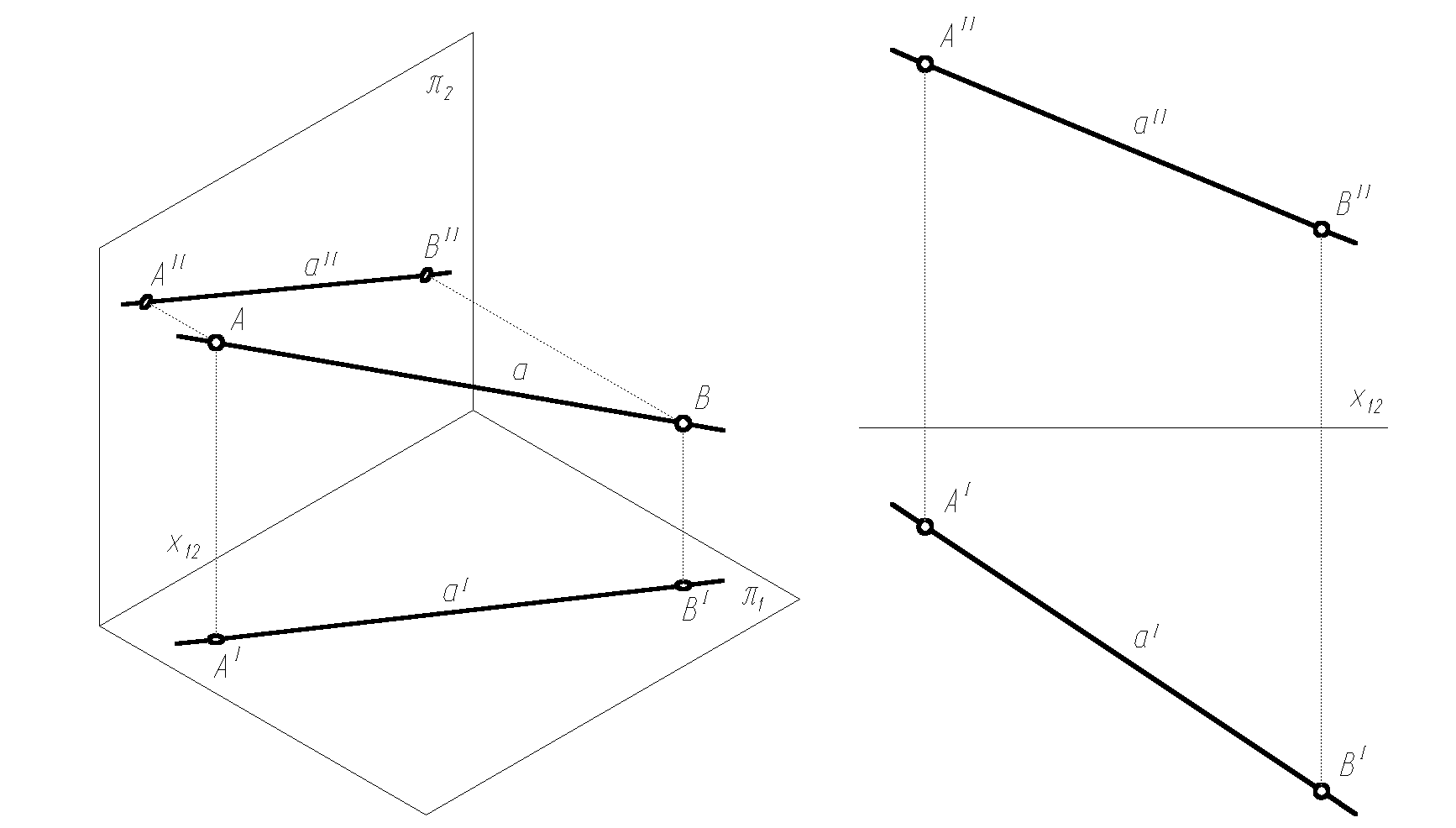
W ogólnym przypadku, gdy prosta nie jest równoległa ani prostopadła do żadnej z rzutni, obydwa rzuty prostej a (a^I, a^II) nie są równoległe do osi rzutów (rys. 1.3). Prostą taką często nazywamy prostą ogólną.

Rys. 1.3

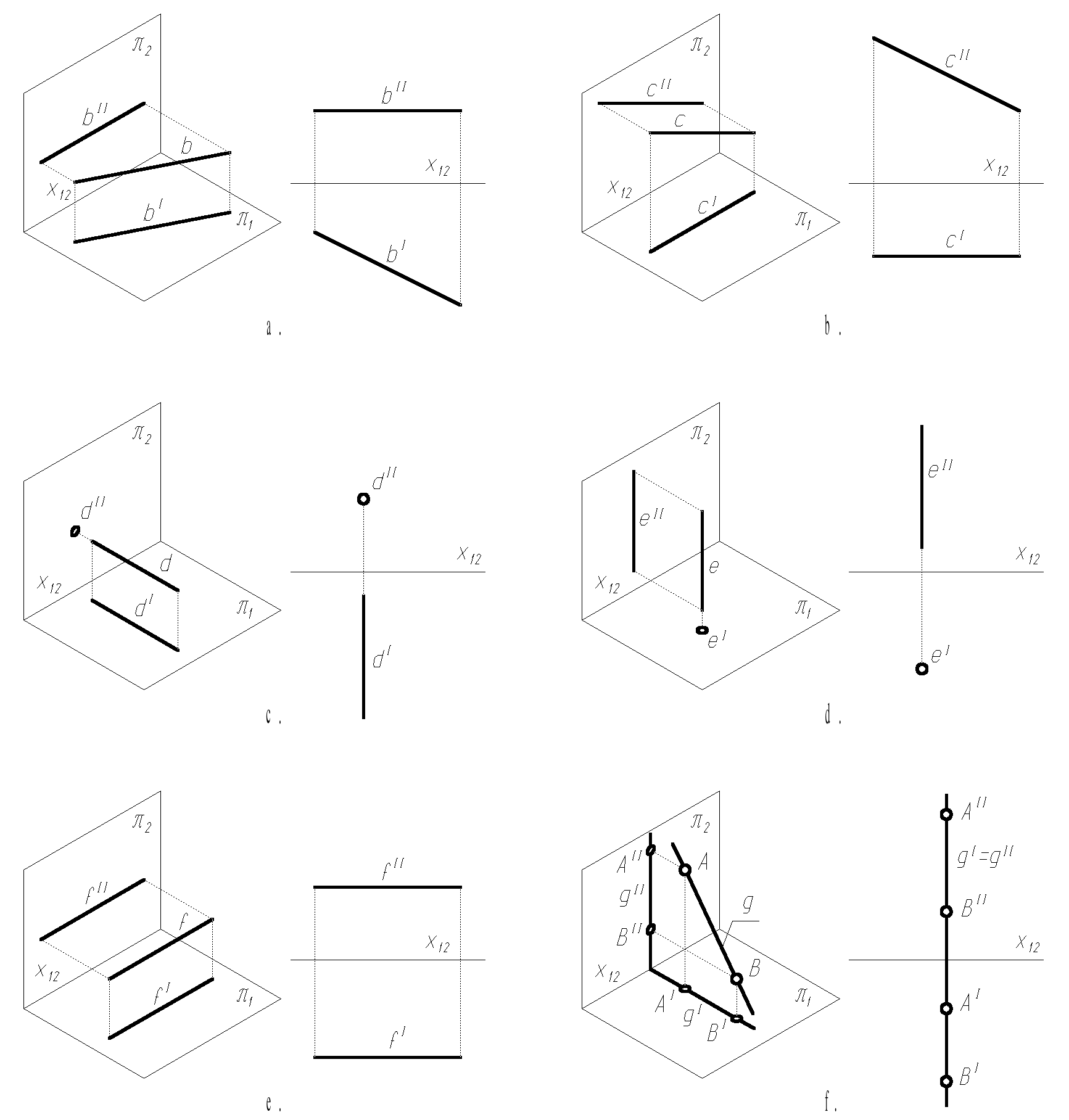
Szczególne przypadki położenia prostej względem rzutni są następujące:

• prosta pozioma - równoległa do rzutni poziomej; jej rzut pionowy b^II jest równoległy do osi rzutów, zaś rzut poziomy b^I przyjmuje położenie dowolne (rys. 1.4a),

• prosta czołowa - równoległa do rzutni pionowej; jej rzut poziomy c^I jest równoległy do osi rzutów, zaś rzut pionowy c^II przyjmuje położenie dowolne (rys. 1.4b),

• prosta celowa - prostopadła do rzutni pionowej, a zarazem równoległa do rzutni poziomej, odmiana prostej poziomej; rzut pionowy d^II jest punktem, a rzut poziomy d^I jest prostopadły do osi rzutów (rys. 1.4c),

• prosta pionowa - prostopadła do rzutni poziomej, a zarazem równoległa do rzutni pionowej, odmiana prostej czołowej; rzut poziomy e^II jest punktem, a rzut pionowy e^I jest prostopadły do osi rzutów (rys. 1.4d),

• prosta równoległa do obydwu rzutni, jednocześnie i pozioma i czołowa; obydwa rzuty prostej (f^I, f^II) są równoległe do osi rzutów (rys. 1.4e),

• prosta prostopadła do osi rzutów, lecz nieprostopadła do żadnej rzutni - rzuty prostej jednoczą się (g^I = g^II) i są prostopadłe do osi rzutów; położenie tej prostej w przestrzeni może być jednoznacznie określone tylko przez rzuty dwóch różnych jej punktów (nie wystarczą same rzuty prostej, rys. 1.4f).

Rys. 1.4

3. Rzuty płaszczyzny

Płaszczyznę wyznaczają:

• trzy punkty nie leżące na jednej prostej (rys. 1.5),

• prosta i punkt nie leżący na tej prostej (rys. 1.6),

• dwie proste przecinające się w punkcie właściwym (rys. 1.7) lub niewłaściwym (czyli równoległe, rys. 1.8).

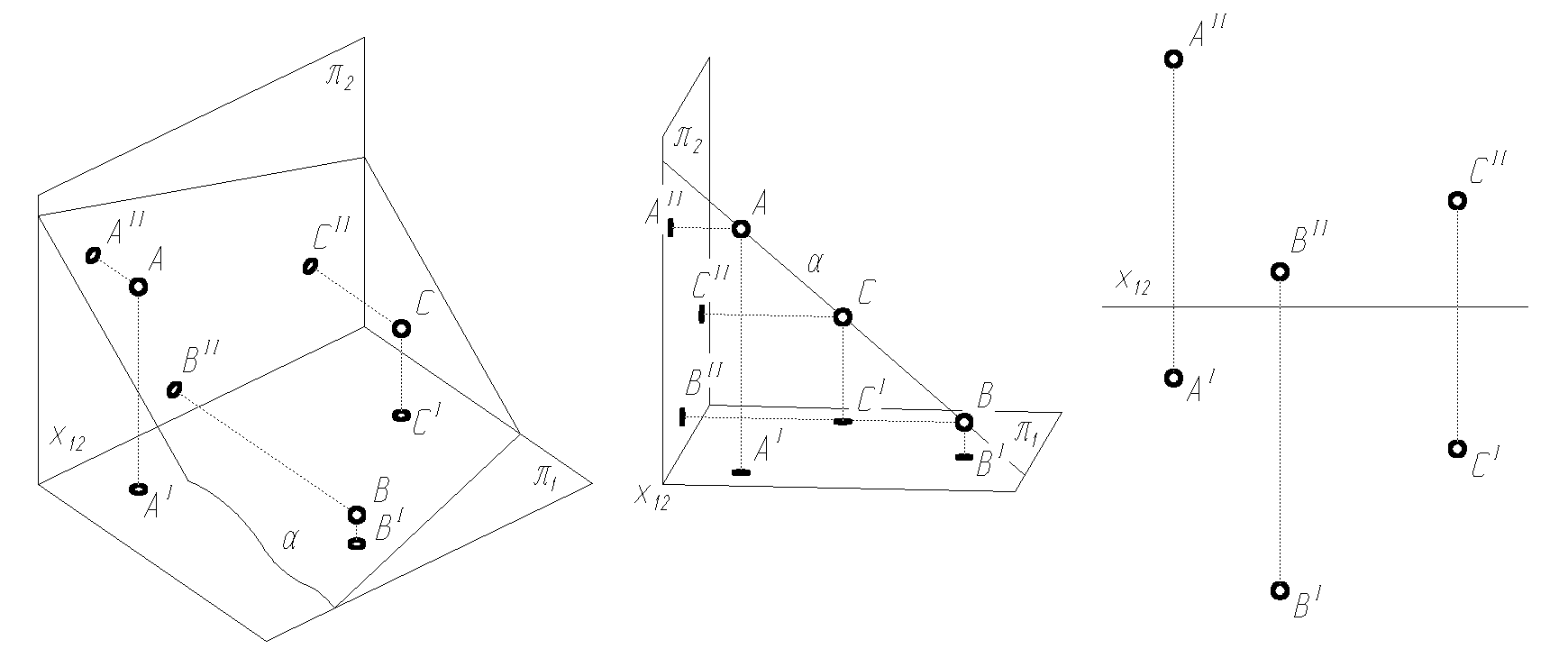
Rys. 1.5

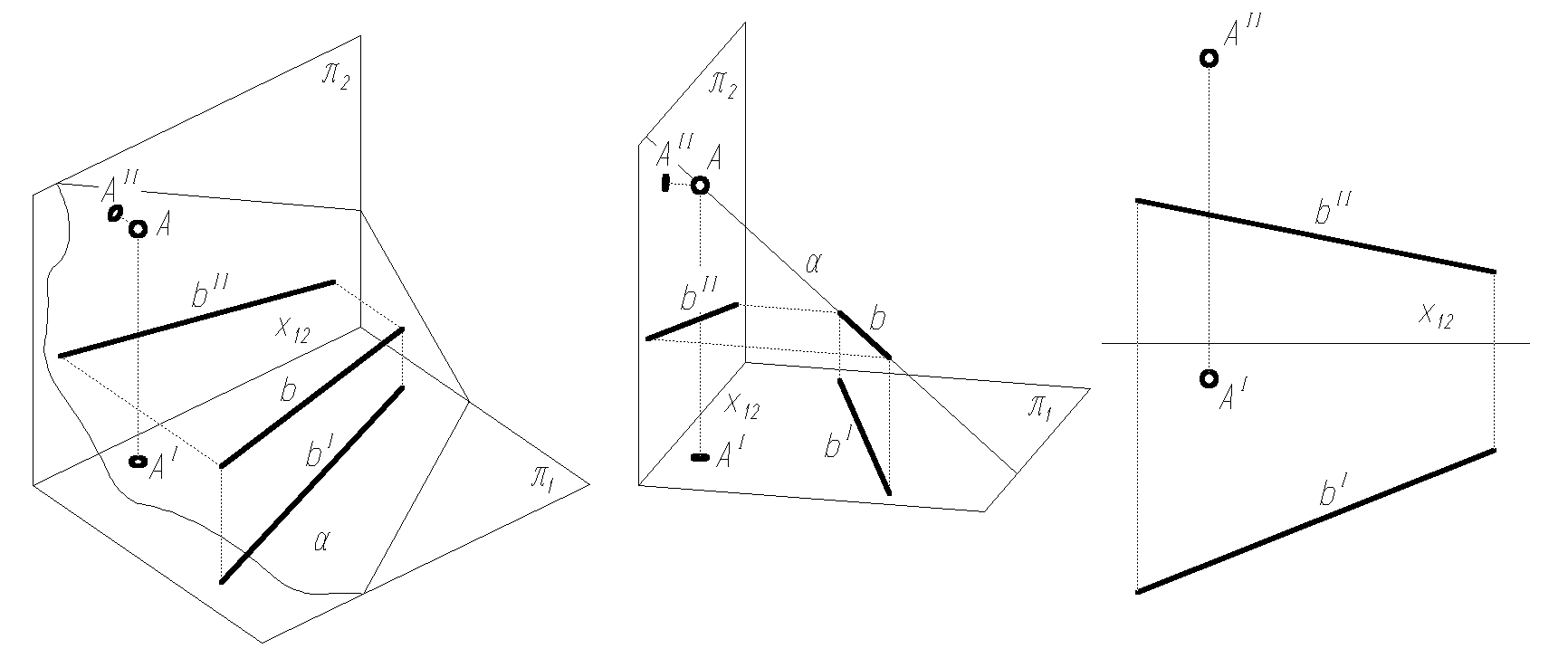
Rys. 1.6

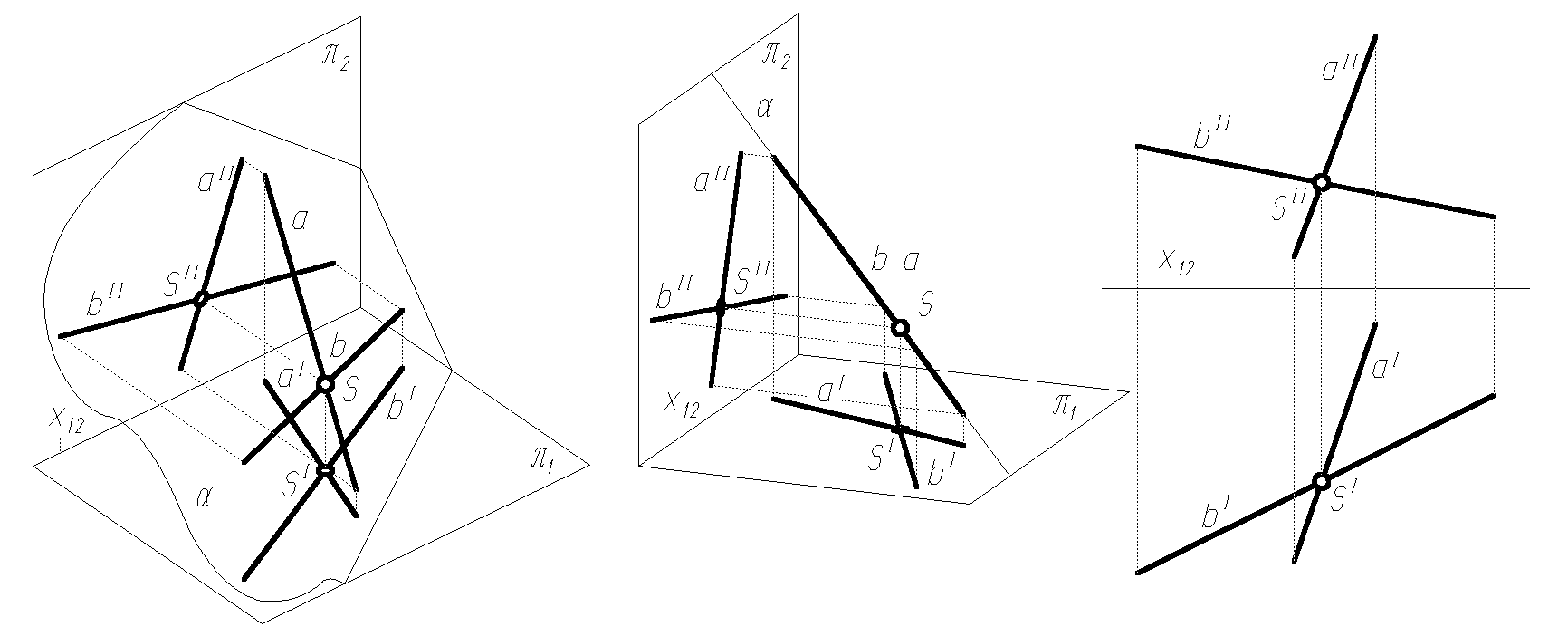
Rys. 1.7

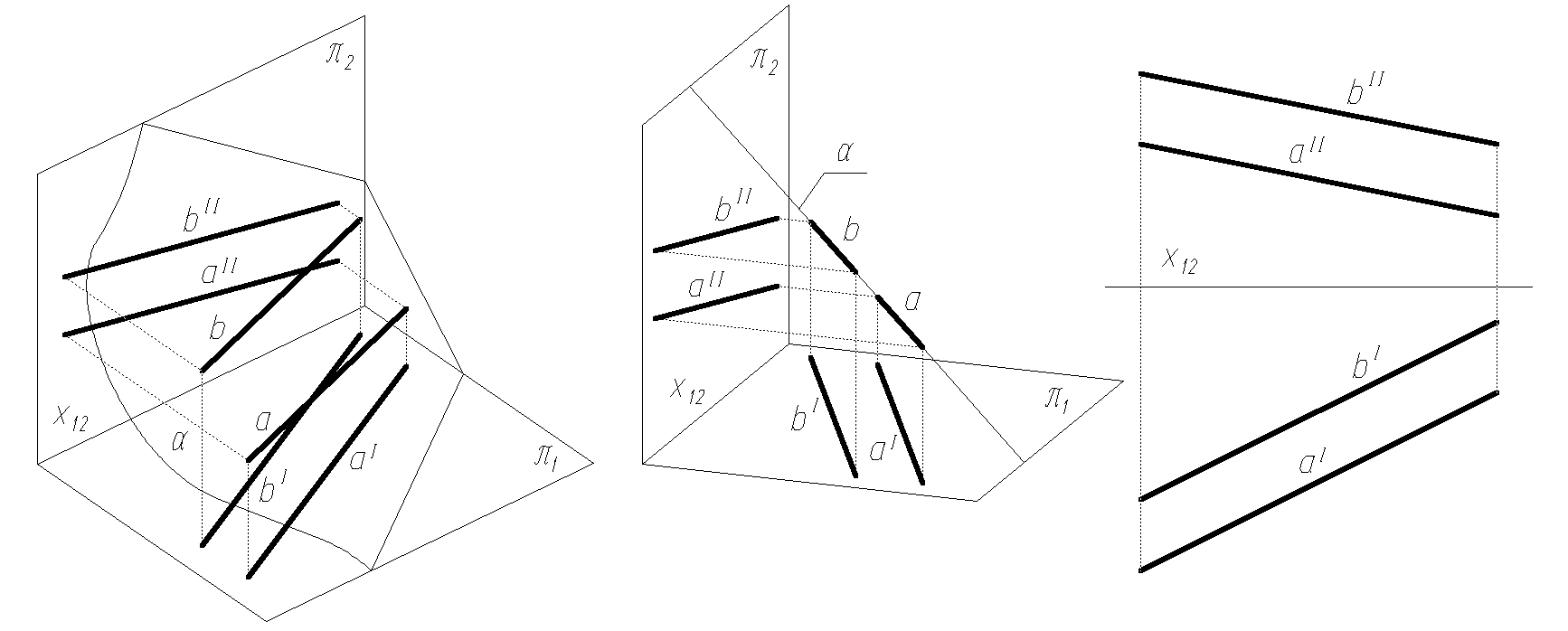
Rys. 1.8

W ogólnym przypadku, gdy płaszczyzna nie jest prostopadła do żadnej z rzutni, rzutami płaszczyzny są wszystkie punkty rzutni i o położeniu płaszczyzny informują nas rzuty elementów na niej leżących (punktów, prostych, figur, albo krzywych płaskich). Płaszczyznę taką nazywamy płaszczyzną ogólną. Szczególne przypadki położenia płaszczyzny względem rzutni to:

• płaszczyzna poziomo rzutująca - prostopadła do rzutni poziomej; jej rzutem poziomym jest prosta α^I, a rzutem pionowym wszystkie punkty rzutni (rys. 1.9a),

• płaszczyzna pionowo rzutująca - prostopadła do rzutni pionowej; jej rzutem pionowym jest prosta β^II, a rzutem poziomym wszystkie punkty rzutni (rys. 1.9b),

• płaszczyzna czołowa - równoległa do rzutni pionowej, odmiana płaszczyzny poziomo rzutującej; jej rzut poziomy, prosta γ^I, jest równoległy do osi rzutów, zaś rzutem pionowym są wszystkie punkty rzutni (rys. 1.9c),

• płaszczyzna pozioma (warstwowa) - równoległa do rzutni poziomej, odmiana płaszczyzny pionowo rzutującej; jej rzut pionowy ε^II jest równoległy do osi rzutów, zaś rzutem poziomym są wszystkie punkty rzutni (rys. 1.9d),

• płaszczyzna prostopadła do obydwu rzutni, jednocześnie poziomo i pionowo rzutująca; jej rzuty, proste δ^I i δ^II, jednoczą się i są prostopadłe do osi rzutów (rys. 1.9e).

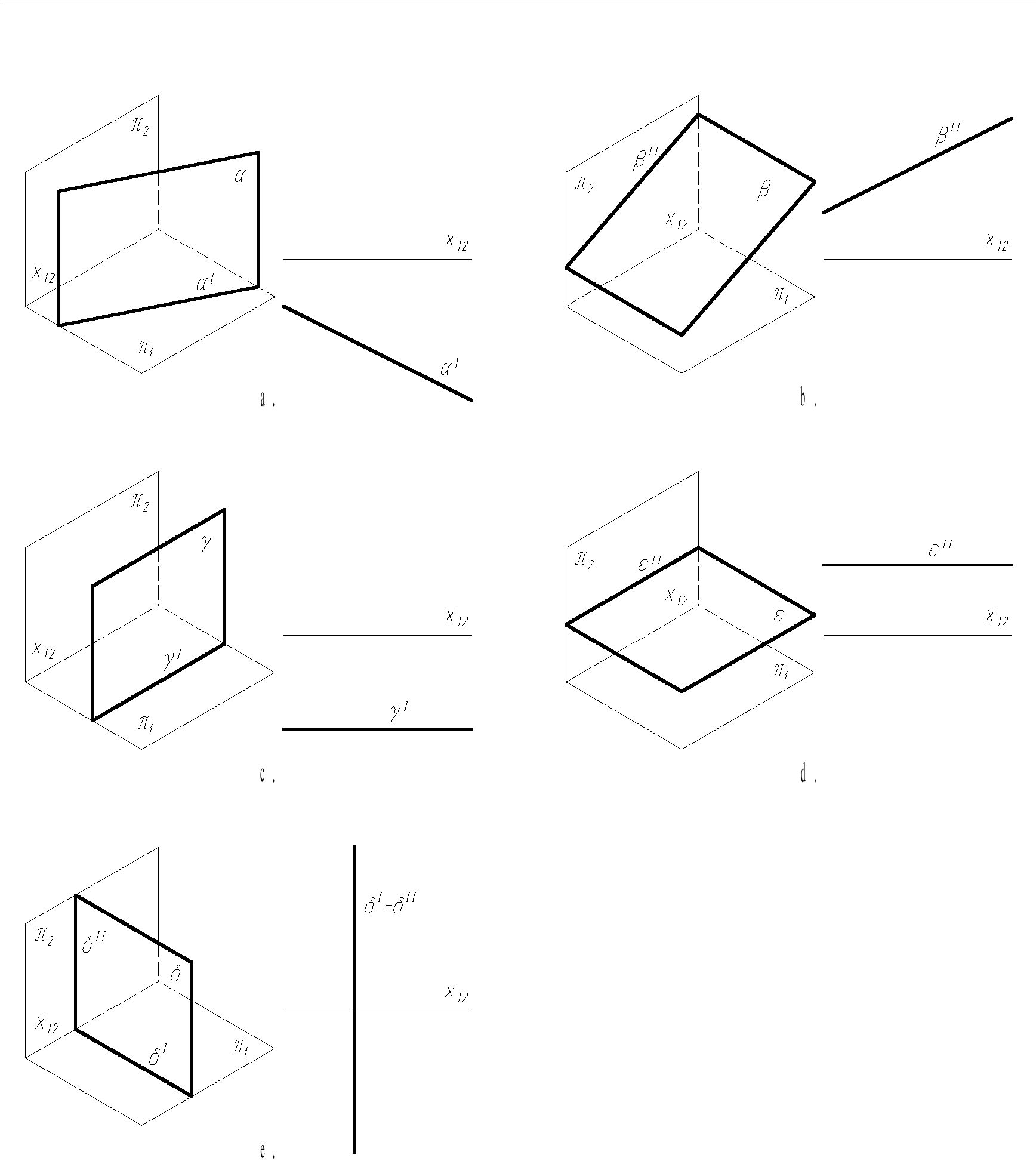
Rys. 1.9

1. Rzuty prostych charakterystycznych leżących w płaszczyźnie trójkąta

Zadanie:

Wykreślić rzuty trójkąta ABC dla zadanych współrzędnych punktów: A(x_A,y_A,z_A), B(x_B,y_B,z_B), C(x_C,y_C,z_C) oraz rzuty prostych charakterystycznych (poziomej i czołowej) leżących w płaszczyźnie trójkąta i przechodzących przez punkt C (rys. 1.10, 1.11).

Rozwiązanie zadania:

1. Kreślimy rzuty trójkąta ABC według zasad opisanych w pkt. 1.1.

2. Przez rzut pionowy punktu C (C^II), równolegle do osi rzutów x_12., kreślimy pionowy rzut prostej poziomej p (p^II).

3. Prosta p przecina bok AB w punkcie 1, czyli prosta p^II przecina odcinek A^IIB^II w punkcie 1^II.

4. Prowadzimy odnoszącą przez punkt 1^II i w przecięciu odnoszącej z odcinkiem A^IB^I znajdujemy poziomy rzut punktu 1 (1^I).

5. Przez punkty C^I i 1^I kreślimy poziomy rzut prostej poziomej (p^I).

6. Przez rzut poziomy punktu C (C^I), równolegle do osi rzutów x_12., rysujemy poziomy rzut prostej czołowej c (c^I).

7. Prosta c przecina bok AB w punkcie 2, więc prosta c^I przecina odcinek A^IB^I w punkcie 2^I.

8. Prowadzimy odnoszącą przez punkt 2^I i w przecięciu odnoszącej z odcinkiem A^IIB^II znajdujemy pionowy rzut punktu 2 (2^II).

9. Przez punkty C^II i 2^II rysujemy pionowy rzut prostej czołowej (c^II).

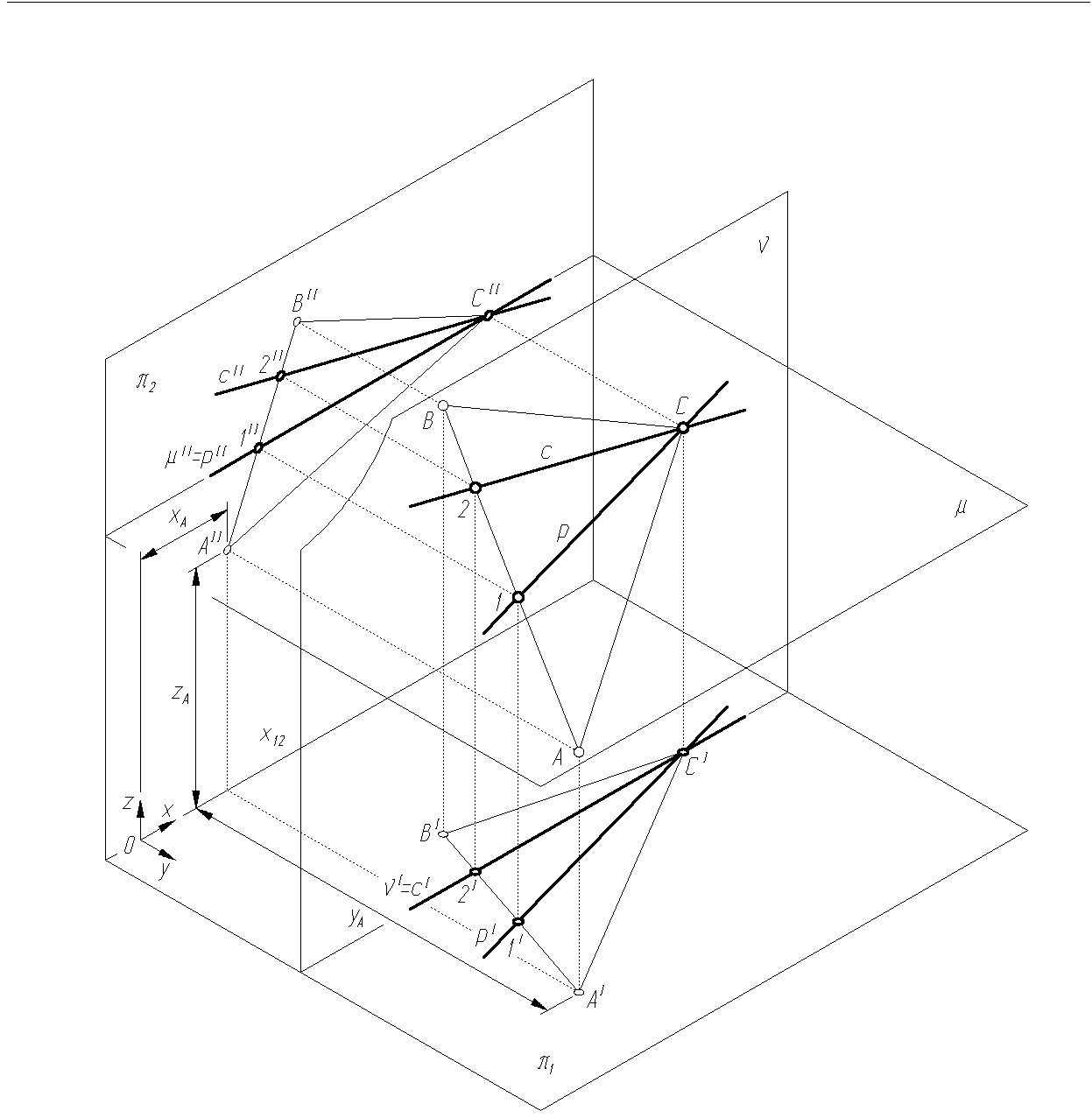
Rys. 1.10

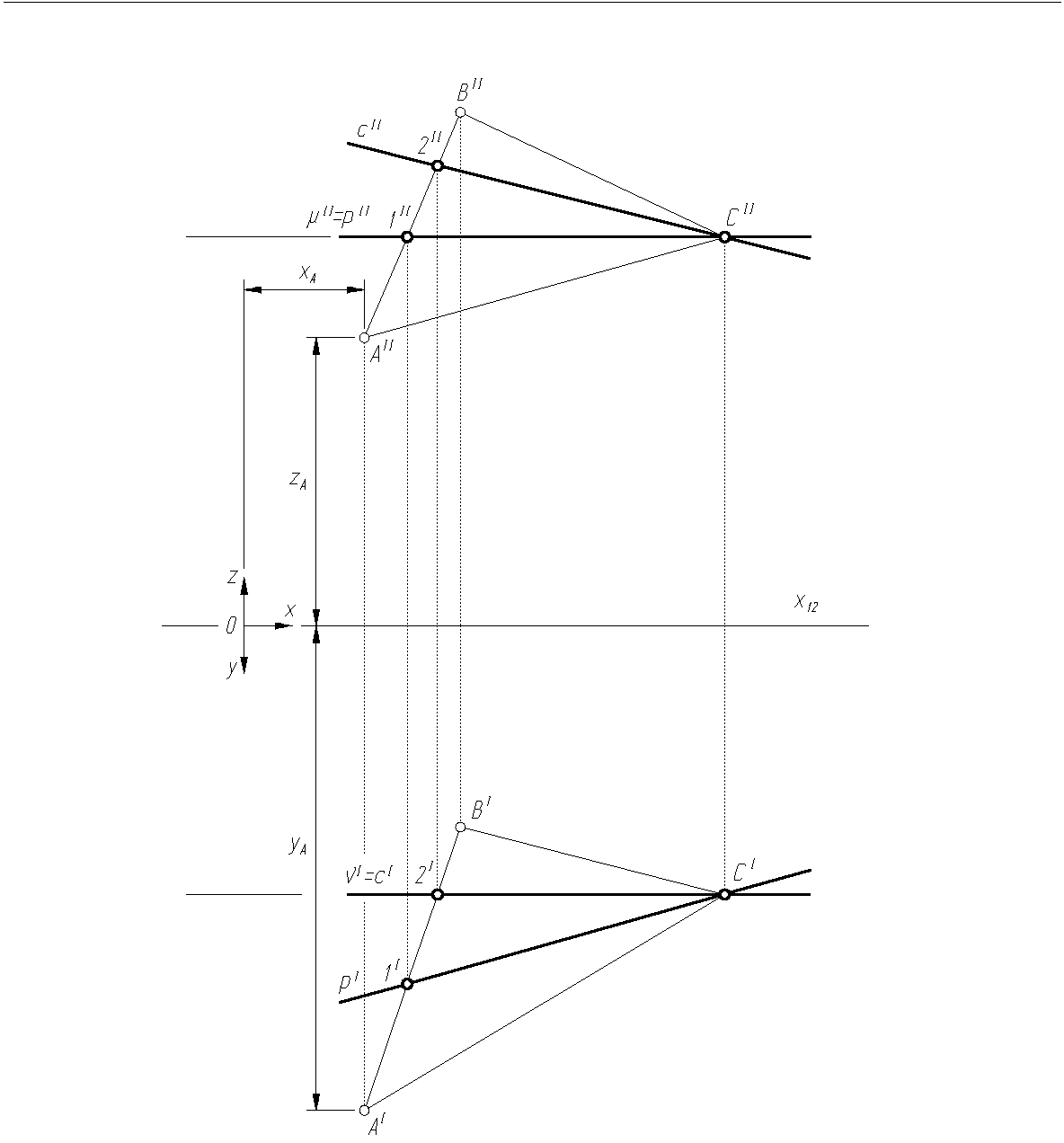
Rys. 1.11

2. Rzuty punktu leżącego w płaszczyźnie trójkąta

Zadanie:

Znaleźć brakujący rzut poziomy punktu P (P^I), leżącego w płaszczyźnie trójkąta ABC, gdy dany jest jego rzut pionowy P^II (rys. 1.12, 1.13).

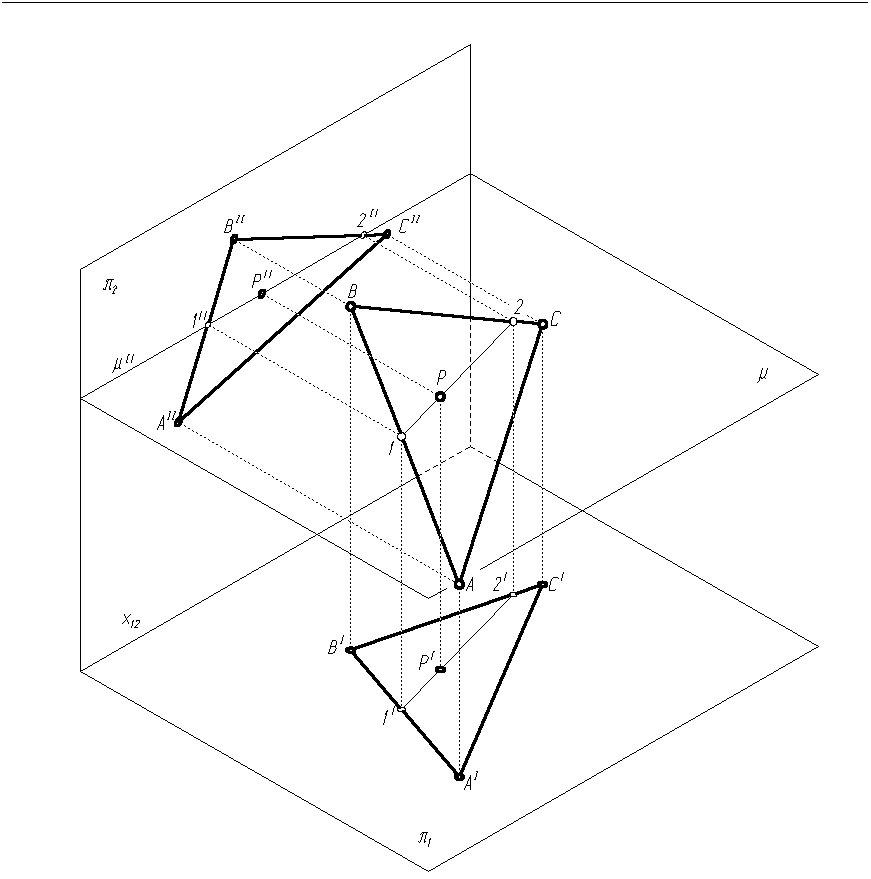
Rys. 1.12

Rozwiązanie zadania:

1. Kreślimy rzuty trójkąta ABC oraz pionowy rzut punktu P (P^II) według zasad opisanych w pkt. 1.1.

2. Przez punkt P^II kreślimy prostą będącą pionowym rzutem prostej poziomej leżącej w płaszczyźnie trójkąta ABC. Prosta ta leży w płaszczyźnie μ równoległej do rzutni poziomej π₁, więc jej rzut pionowy jest równoległy do osi rzutów x_12.. Prosta przecina bok AB w punkcie 1, zaś bok BC w punkcie 2 (pionowy rzut prostej przecina odcinek A^IIB^II w punkcie 1^II, a odcinek B^IIC^II w punkcie 2^II).

3. Przez punkty 1^II i 2^II prowadzimy odnoszące, aż do przecięcia z poziomymi rzutami odpowiednich boków trójkąta.

4. W przecięciu odnoszącej z odcinkiem A^IB^I zaznaczamy poziomy rzut punktu 1 (1^I), a w przecięciu odnoszącej z odcinkiem B^IC^I poziomy rzut punktu 2 (2^I).

5. Rysujemy poziomy rzut prostej poziomej przechodzącej przez punkty 1 i 2 (odcinek 1^I2^I).

6. Brakujący rzut poziomy punktu P (P^I) znajdujemy na przecięciu odnoszącej przechodzącej przez punkt P^II z odcinkiem 1^I2^I.

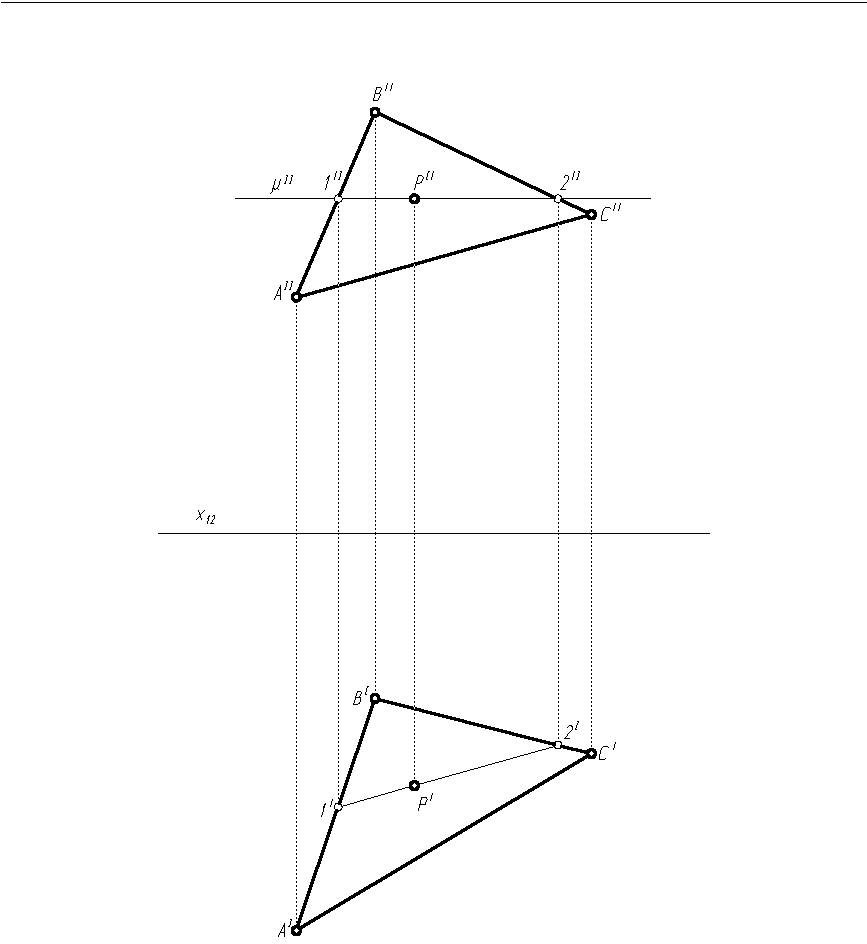
Rys. 1.13

3. Przekrój trójkąta płaszczyzną rzutującą

Zadanie:

Trójkąt ABC przecięto płaszczyzną poziomo rzutującą α przechodzącą przez punkty K i L. Narysować rzuty krawędzi przecięcia oraz określić, która część trójkąta zostanie zasłonięta przez płaszczyznę α (rys. 1.14, 1.15).

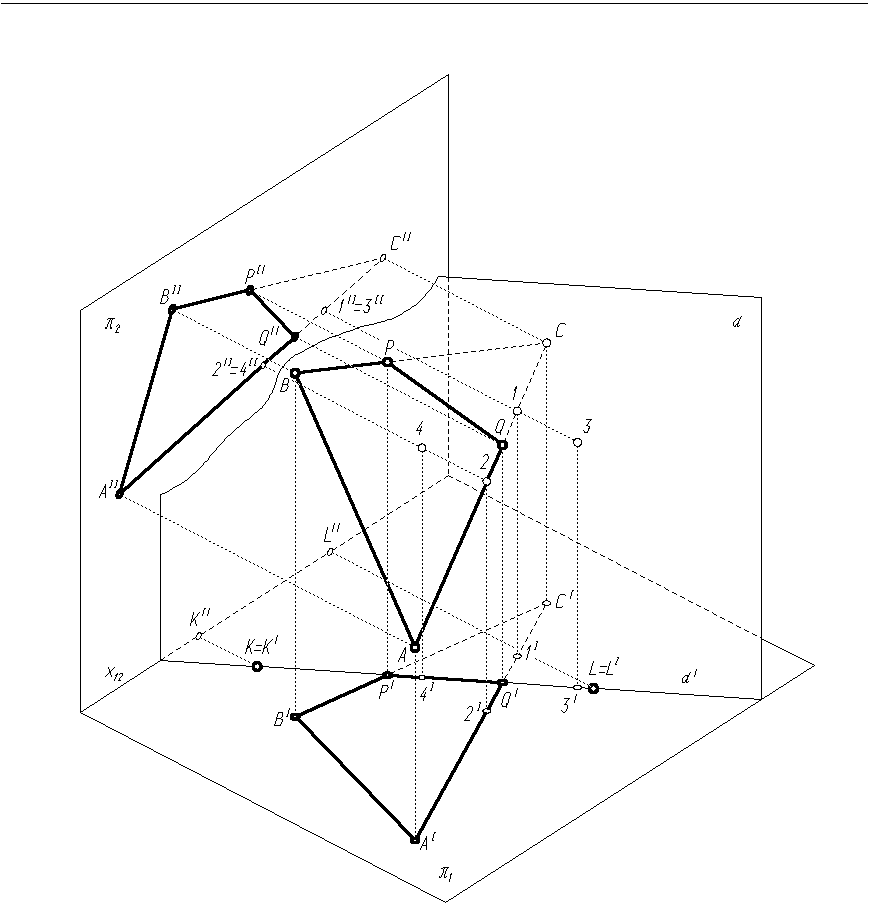
Rys. 1.14

Rozwiązanie zadania:

1. Kreślimy rzuty trójkąta ABC oraz poziomy rzut płaszczyzny α (prosta α^I przechodząca przez punkty K^I i L^I).

2. Na poziomym rzucie płaszczyzny α rysujemy poziome rzuty punktów przebicia płaszczyzny przez boki trójkąta: P^I w przecięciu α^I z odcinkiem B^IC^I oraz Q^I w przecięciu α^I z odcinkiem A^IC^I.

3. Znajdujemy pionowe rzuty punktów przebicia P^II i Q^II poprzez odrzutowanie punktów P^I i Q^I na pionowe rzuty odpowiednich boków trójkąta.

4. Łączymy liniami prostymi punkty P^I i Q^I oraz P^II i Q^II. Odcinek PQ łączący punkty przebicia jest krawędzią przecięcia płaszczyzny trójkąta ABC przez płaszczyznę

5. Określenie widoczności trójkąta w rzucie pionowym polega na sprawdzeniu, który z punktów leżących na boku AC w najbliższym otoczeniu punktu przebicia Q (albo na boku BC w otoczeniu punktu P), jest zasłonięty przez płaszczyznę α. W tym celu zaznaczamy rzuty dwóch dowolnych punktów 1 i 2 leżących na odcinku AC. Następnie w płaszczyźnie α znajdujemy rzuty punktów 3 i 4, które mają taką samą wysokość (współrzędna z) i szerokość (współrzędna x), co punkty 1 i 2. Rzuty pionowe punktów 1 i 3 oraz 2 i 4 jednoczą się (1^II = 3^II, 2^II = 4^II). Sprawdzamy, który z punktów każdej pary ma większą głębokość (współrzędną y). W rzucie pionowym widoczny jest ten punkt, którego głębokość jest większa (zgodnie z europejskim systemem rzutowania przedmiot znajduje się między rzutnią a obserwatorem). W naszym przypadku widoczny jest punkt 2, leżący z lewej strony punktu Q. Punkt 1, położony z prawej strony punktu przebicia, jest zasłonięty przez punkt 3 leżący w płaszczyźnie tnącej. Wynika stąd, że odcinek QC jest również zasłonięty przez płaszczyznę α, a wraz z nim także odcinek PC.

6. W rzucie poziomym cały trójkąt jest widoczny, bo rzutem płaszczyzny α jest prosta, która nie może zasłonić żadnego fragmentu trójkąta.

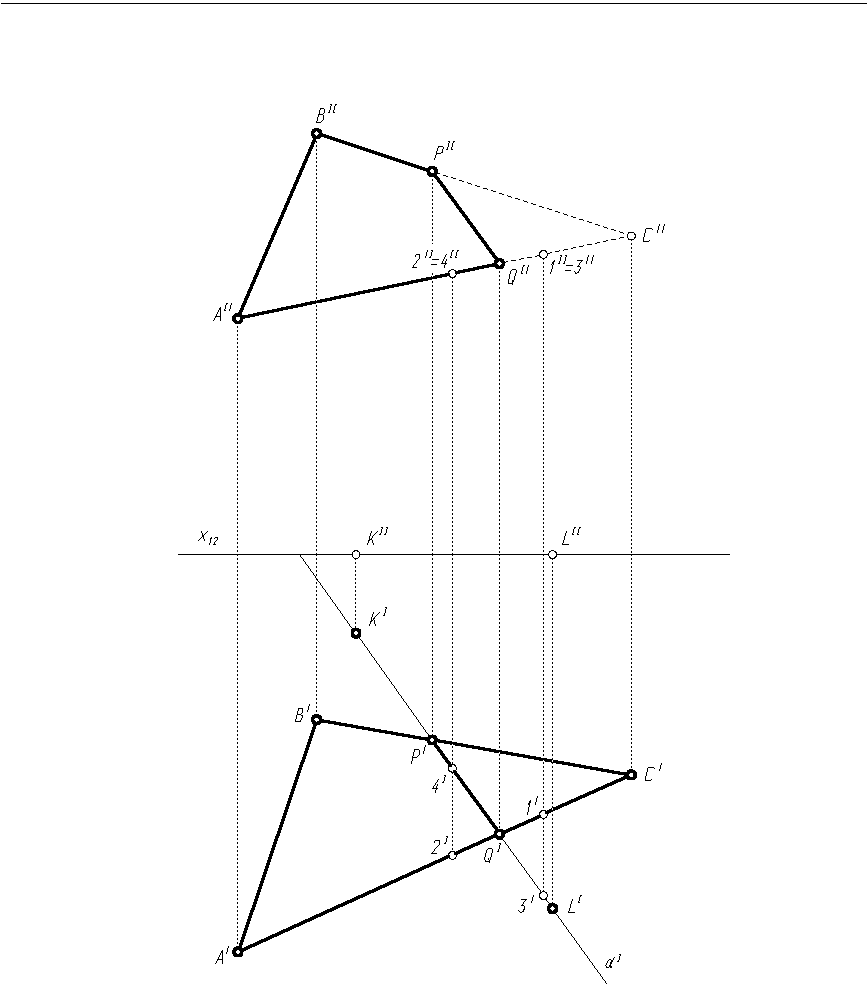
Rys. 1.15

10

Politechnika Łódzka, Katedra Konstrukcji Precyzyjnych

9

Materiały pomocnicze do Geometrii Wykreślnej

---