9. Geometria przewodów i ich rozwinięć

1. Kolano o zmiennym przekroju

Zadanie:

Zaprojektować kolano (łącznik) o zmiennym przekroju łączący dwa, ustawione pod kątem prostym, przewody o średnicach D₁ i D₂. Promień kolana wynosi R. Należy również wykonać rozwinięcie powierzchni łącznika.

a. b.

Rys. 9.1

Rozwiązanie zadania:

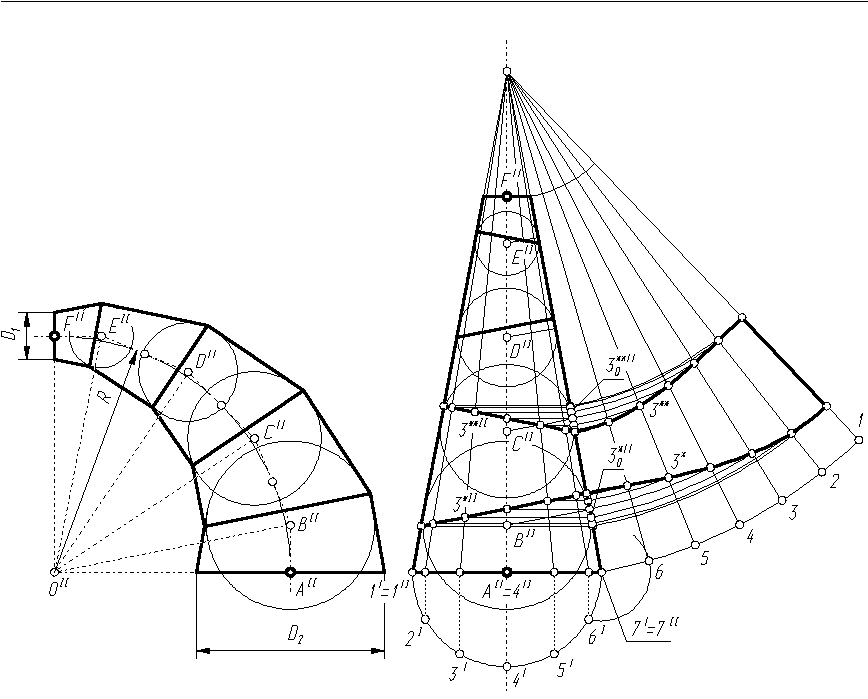
1. Kreślimy łuk okręgu o promieniu R (równym promieniowi łącznika) i końcach w punktach A i F (rys. 9.1a i 9.4). Łuk ten dzielimy na pewną ilość równych części. W omawianym zadaniu łuk podzielono na cztery części (punktów podziału nie opisano).

2. W punktach podziału, a także w punktach A i F, prowadzimy styczne do łuku. Styczne te przecinają się w punktach B, C, D i E.

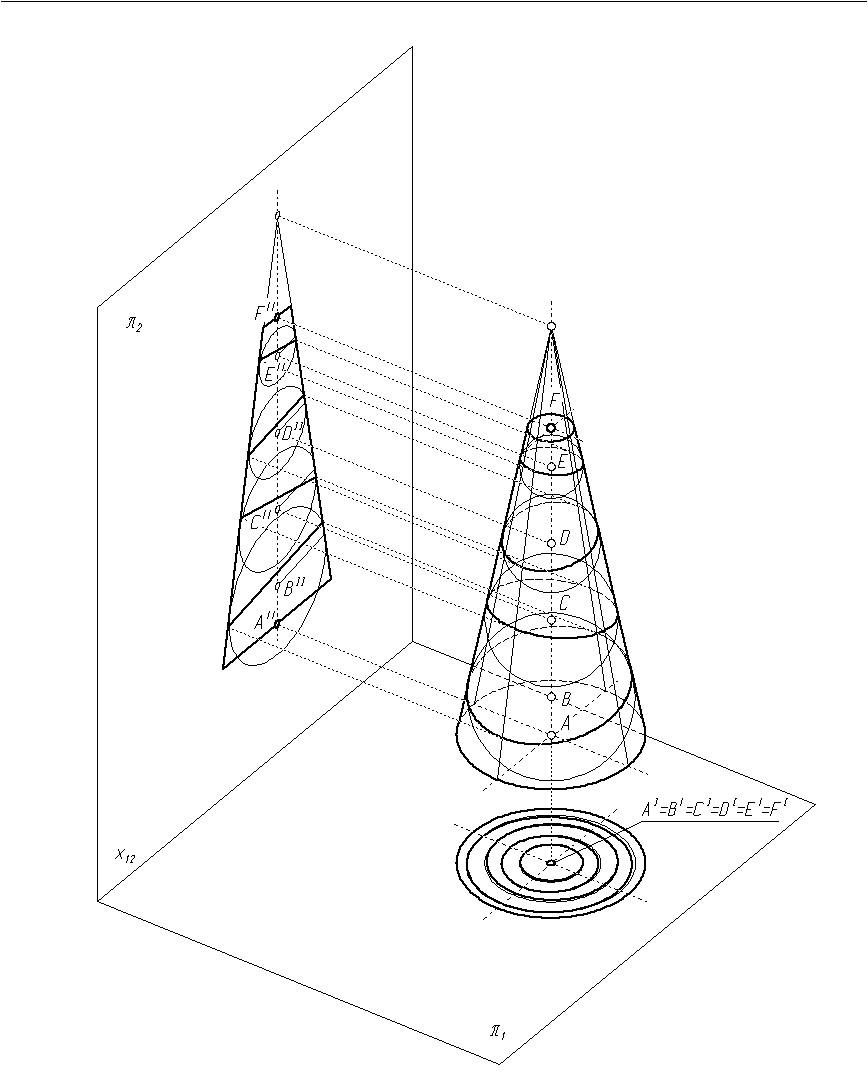
3. Na dowolnie obranej prostej (rys. 9.1b i 9.2) odkładamy odcinki: AB, BC, CD, DE i EF. Narysowana prosta jest osią obrotowej powierzchni stożkowej wyznaczonej przez okręgi o środkach A i F oraz średnicach równych średnicom łączonych przewodów.

4. W otrzymaną powierzchnię stożkową wpisujemy kule o środkach B, C, D i E. Ich pionowymi rzutami są okręgi o środkach B^II, C^II, D^II i E^II styczne do prostych będących konturami powierzchni stożkowej w rzucie pionowym (rys. 9.1b).

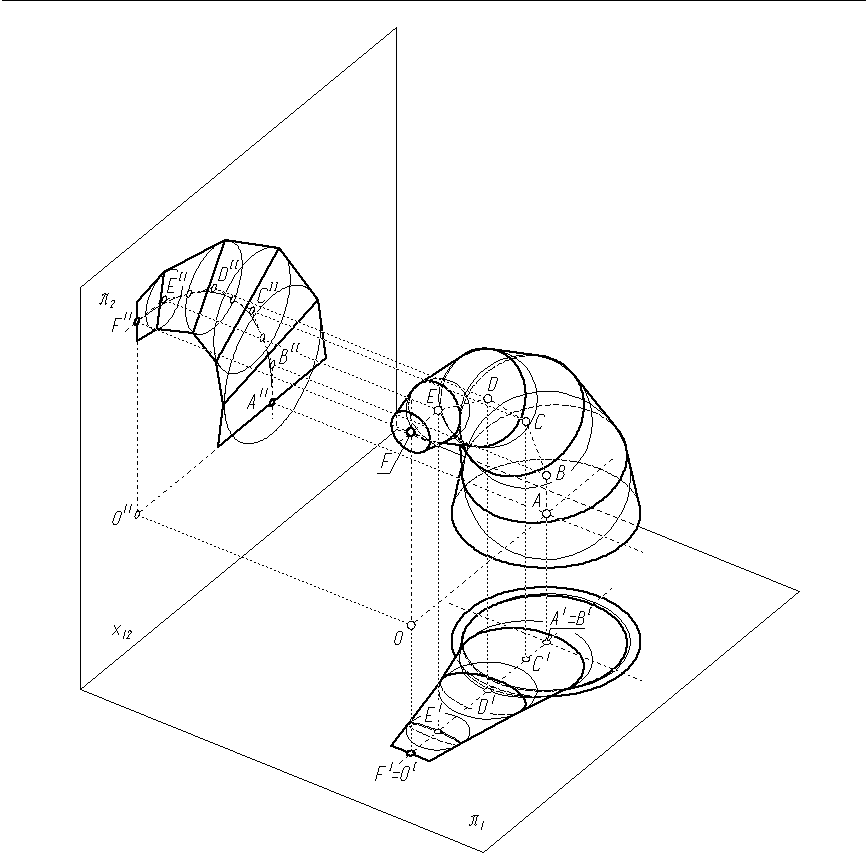
5. Wracamy do rysunku 9.1a i rysujemy przystające okręgi, których środkami są odpowiednie wierzchołki: B^II, C^II, D^II i E^II łamanej A^IIB^IIC^IID^IIE^IIF^II. Okręgi te są rzutami pionowymi kul o środkach w wierzchołkach łamanej ABCDEF, na których opisane są powierzchnie segmentów łącznika (rys. 9.4). Pierwszy segment wyznaczony jest przez okrąg o średnicy D₂ i środku w punkcie A oraz kulę o środku w punkcie B. Drugi, trzeci i czwarty, odpowiednio, przez kule o środkach w punktach: B i C, C i D oraz D i E. Ostatni, piąty segment wyznacza kula o środku w punkcie E oraz okrąg o średnicy D₁ i środku w punkcie F. Kąty rozwarć skonstruowanych w ten sposób segmentów są równe. Liniami czołowych połączeń powierzchni segmentów są elipsy. Wierzchołki tych elips są punktami przecięcia tworzących konturowych odpowiednich segmentów. Tworzące konturowe segmentów wyznacza się, kreśląc styczne do okręgów będących rzutami pionowymi kul (rys. 9.1a).

Rys. 9.2

Rys. 9.3

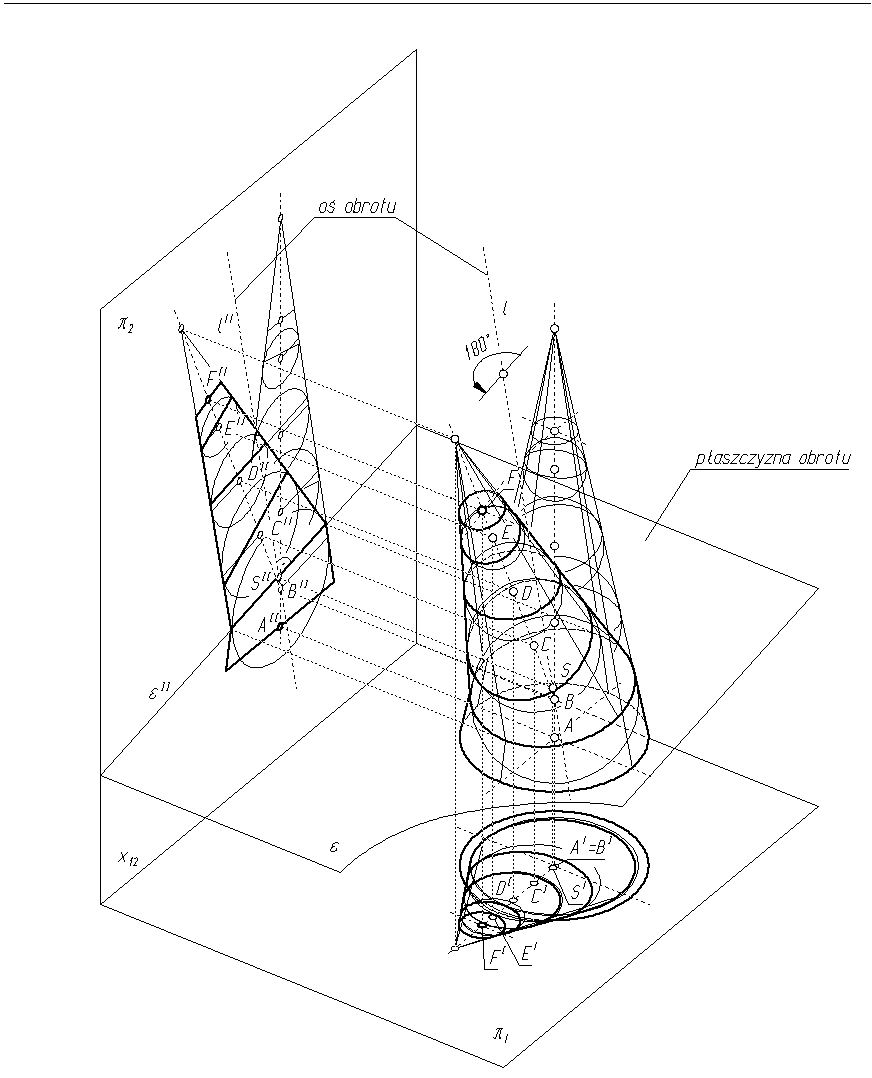
6. Rozwinięcie wyznaczonych w ten sposób segmentów łącznika najdogodniej jest wykonać, nakładając segmenty na pomocniczą powierzchnię stożkową (rys. 9.2). Najpierw na powierzchnię stożkową nakładamy pierwszy segment (wyznaczony przez okrąg o średnicy D₂ i środku w punkcie A oraz kulę o środku w punkcie B). Kreśląc rzut pionowy pierwszego segmentu, odkładamy na tworzących konturowych powierzchni stożkowej, z punktów 1^II i 7^II, odcinki o długościach równych długościom odpowiednich tworzących konturowych segmentu (rys. 9.1b). Drugi segment nakładamy, obracając go o 180° dookoła osi przechodzącej przez środek elipsy, będącej linią czołowego połączenia segmentu drugiego i pierwszego, i prostopadłej do płaszczyzny tego połączenia. (Postępując odwrotnie, można z segmentów nałożonych na powierzchnię stożkową otrzymać powierzchnię projektowanego kolana - patrz: rys. 9.3). W związku z tym, wykreślenie rzutu pionowego drugiego segmentu polega na  narysowaniu jego wewnętrznej (leżącej po wklęsłej stronie łącznika) tworzącej konturowej na  przedłużeniu zewnętrznej tworzącej konturowej pierwszego segmentu, zaś zewnętrznej - na  przedłużeniu wewnętrznej tworzącej konturowej pierwszego segmentu. W analogiczny sposób nakładamy na powierzchnię stożkową pozostałe segmenty.

7. Rozwinięcie powierzchni stożkowej z naniesionymi na niej liniami czołowych połączeń segmentów wykonujemy tak, jak w Przykładzie 5.5. Zalecany sposób wykreślenia rozwinięcia przedstawiono na rysunku 9.1b.

Rys. 9.4

Literatura

1. Polański S., Kowalewski A., Daniluk J.: Geometria dla konstruktorów. Warszawa. WNT 1965.

2. Człon łączący dwa przewody

Zadanie:

Zaprojektować człon łączący przewód o przekroju okrągłym z przewodem o przekroju prostokątnym i wykonać rozwinięcie jego powierzchni. Dane są wymiary łącznika i łączonych przewodów (rys. 9.5):

• średnica przewodu okrągłego: d,

• wymiary przewodu prostokątnego: a × b,

• wysokość łącznika: h,

• przesunięcie płaszczyzn symetrii przewodów: m.

Rozwiązanie zadania:

1. Powierzchnia łącznika utworzona jest z czterech trójkątów: AB4, EF10, AE1 i BF7 oraz z czterech powierzchni stożkowych o wierzchołkach A, B, F, E, których kierownicami są ćwiartki okręgu, określone przez punkty, odpowiednio: 1 i 4, 4 i 7, 7 i 10, 10 i 1. Płaszczyzny trójkątów są styczne do powierzchni stożkowych (rys. 9.5).

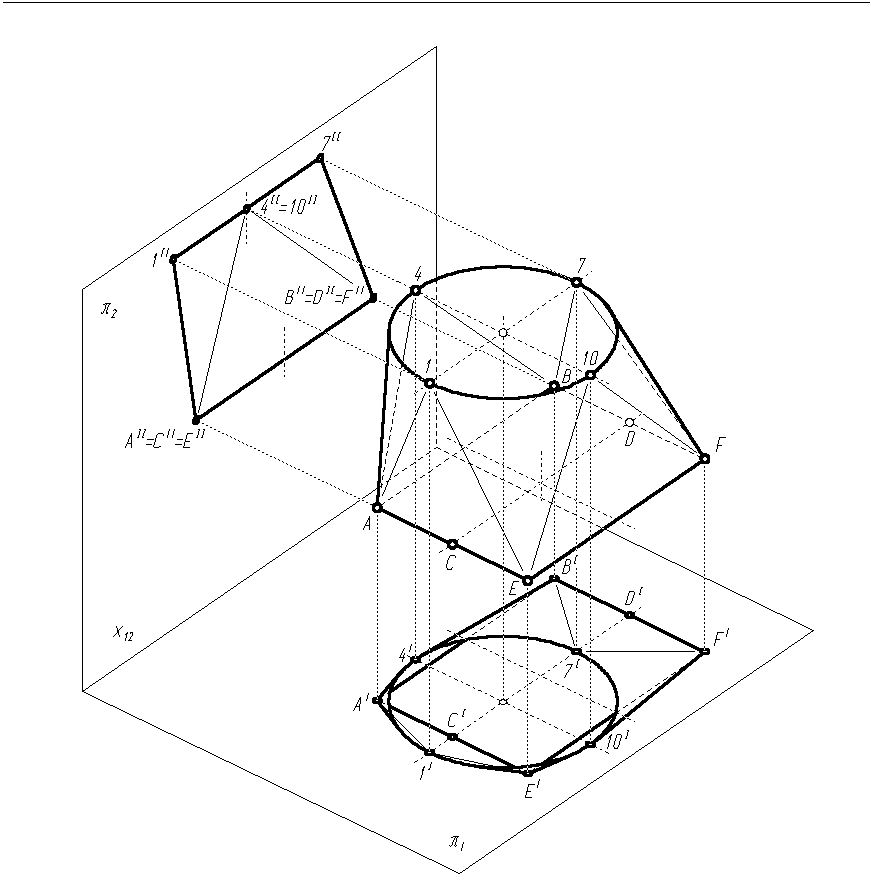
Rys. 9.5

2. Konstrukcję rozwinięcia jednej z dwóch symetrycznych części łącznika rozpoczynamy od wykreślenia trójkąta AB4 (rys. 9.6). Wcześniej należy metodą obrotu znaleźć długości odcinków A4 i B4. Odcinek AB, jako równoległy do rzutni π₁ i π₂, jest w obu rzutach przedstawiony w wielkości rzeczywistej. Z kolei dokonujemy rozwinięć powierzchni stożkowych o wierzchołkach A i B. Rozpatrywane powierzchnie są fragmentami powierzchni stożków nieobrotowych, więc ich rozwinięcia wykonujemy podobnie, jak w Przykładzie 5.6. Wreszcie wykreślamy trójkąty AC1 i BD7, czyli fragmenty bocznych ścian łącznika. Długości boków AC i BD odmierzamy z rzutu poziomego (odcinki A^IC^I i B^ID^I), a długości boków C1 i D7, będących osiami symetrii ścian bocznych, z rzutu pionowego (odcinki C^II1^II i D^II7^II).

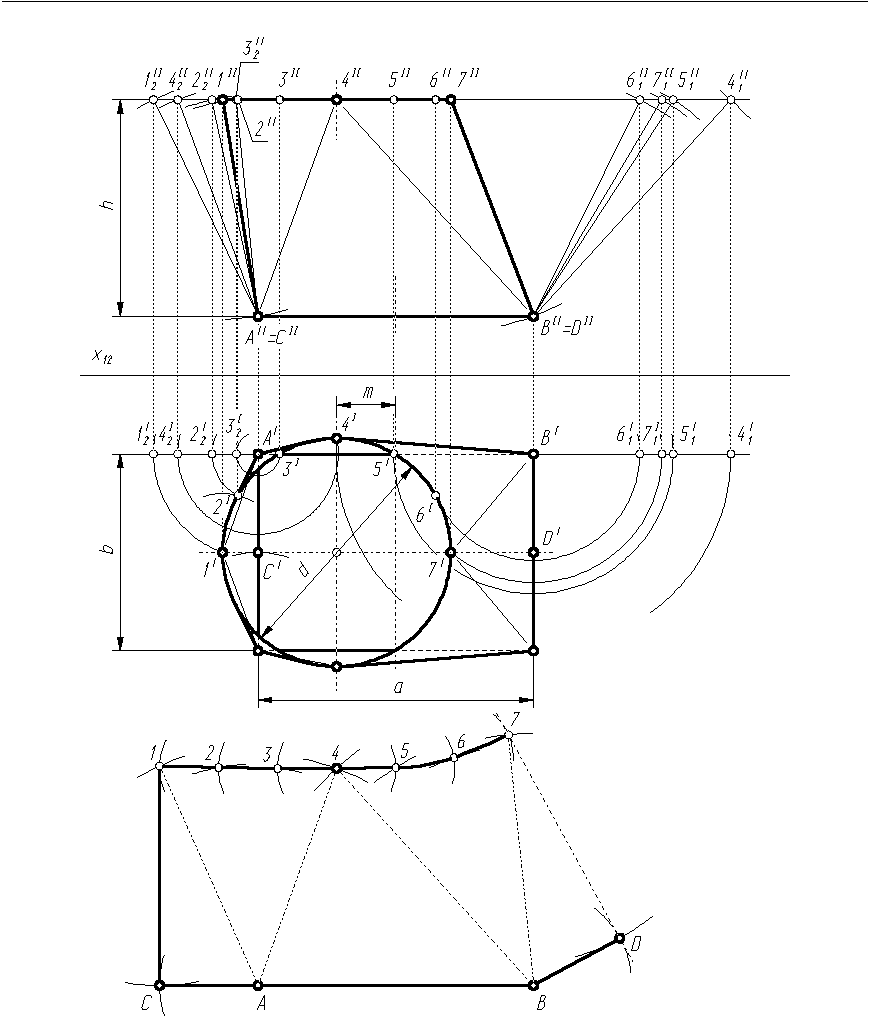
Rys. 9.6

Literatura

1. Polański S., Kowalewski A., Daniluk J.: Geometria dla konstruktorów. Warszawa. WNT 1965.

52

Politechnika Łódzka, Katedra Konstrukcji Precyzyjnych

53

Materiały pomocnicze do Geometrii Wykreślnej

---