2. Wielościan w rzutach Monge'a i izometrii prostokątnej

Wielościanem nazywamy część przestrzeni ograniczoną powierzchnią będącą zbiorem wielokątów. Każdy bok wielokąta jest przy tym wspólny dla dokładnie dwóch wielokątów powierzchni wielościanu. Wielokąty te nazywamy ścianami wielościanu, a ich wierzchołki i boki wierzchołkami i krawędziami wielościanu. Postać wielościanu ma wiele prostych części maszynowych - wsporniki, łączniki, itp.

1. Rysunek części maszynowej w rzutach Monge'a i izometrii prostokątnej

Zadanie:

Na podstawie rzutu aksonometrycznego przedstawionego w izometrii prostokątnej wykreślić trzy rzuty prostokątne (Monge'a) prostej części maszynowej będącej wielościanem (rys. 2.1, 2.2). Rzut trzeci, boczny wykonać na rzutnię π₃ prostopadłą do rzutni poziomej π₁ i pionowej π₂.

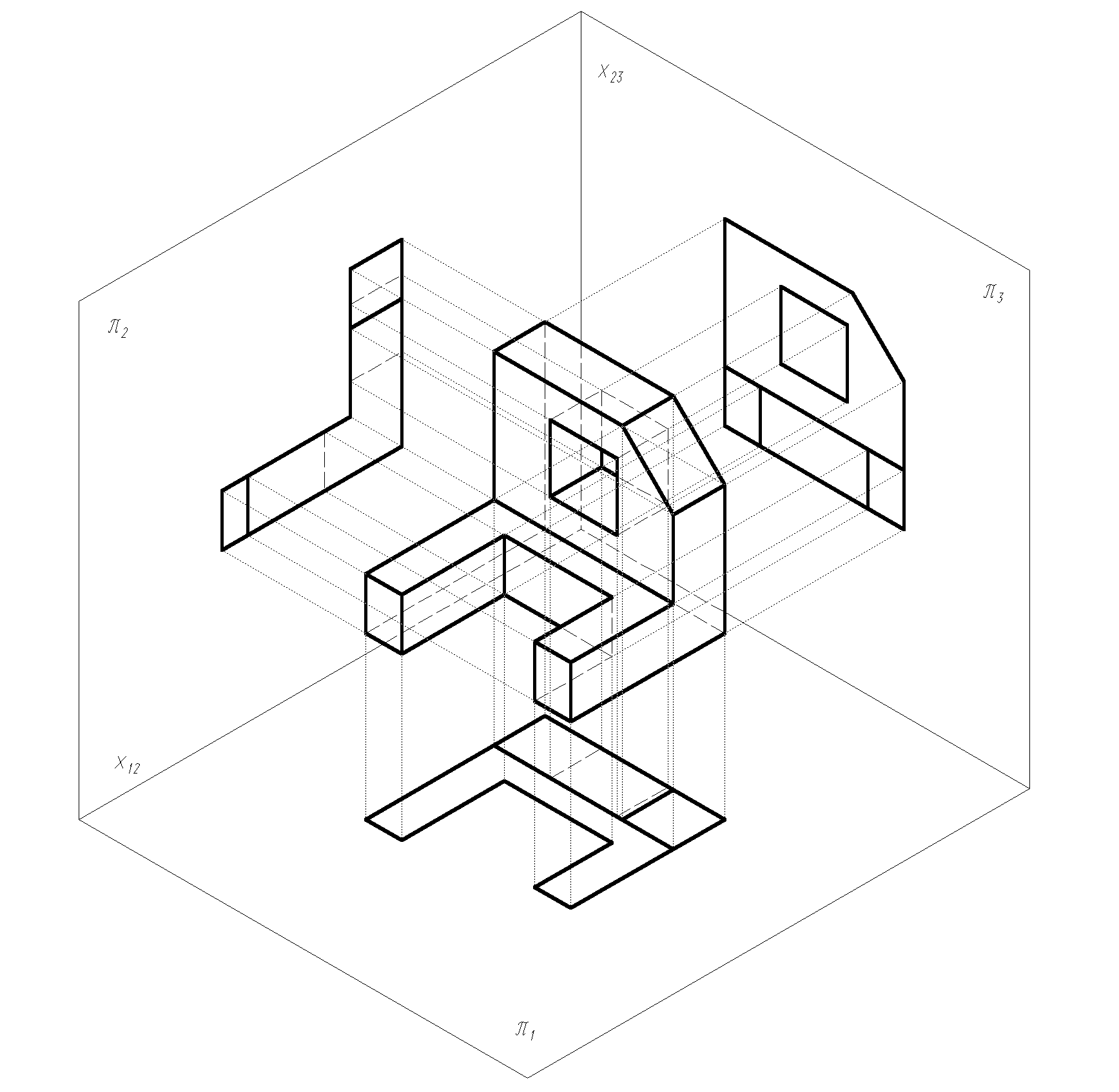
Rys. 2.1

Rozwiązanie zadania:

1. Kreślimy widok aksonometryczny przedmiotu pamiętając o zachowaniu odpowiednich kątów między prostymi równoległymi do osi układu współrzędnych, właściwych dla izometrii prostokątnej (rys. 2.2).

2. Wykreślamy rzuty Monge'a, odpowiadające ustawieniu przedmiotu względem rzutni takiemu jak na rysunku 2.1. Rozwinięty układ trzech rzutni otrzymujemy obracając rzutnię π₁ dookoła osi rzutów x₁₂, a rzutnię π₃ dookoła osi rzutów x₂₃ tak, by zjednoczyły się z płaszczyzną rzutni π₂. Boczny rzut wielościanu wykonujemy według zasad opisanych rozdziale 3. Przy wykreślaniu rzutów trzeba pamiętać o skróceniu aksonometrycznym, które dla izometrii prostokątnej wynosi s ≈ 0,82. Przed narysowaniem rzutu odcinka, jego długość zmierzoną w rzucie aksonometrycznym należy podzielić przez s.

Uwaga: W rzucie aksonometrycznym wolno mierzyć długości tylko tych odcinków, które są równoległe do osi układu współrzędnych.

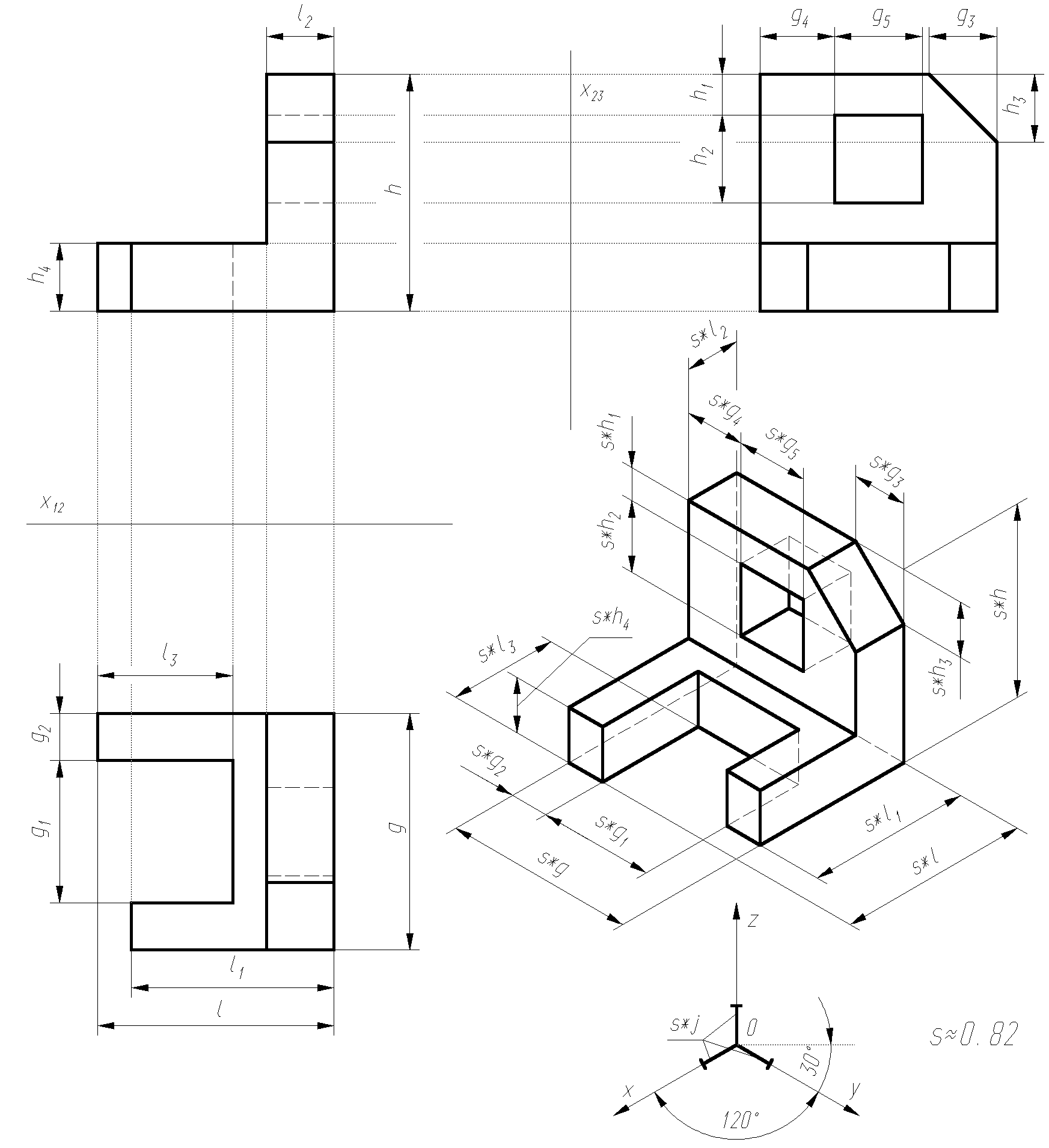
Rys. 2.2

3. Transformacja

Transformacja rzutu, czyli zmiana układu rzutni, polega na wprowadzeniu nowego układu rzutni prostopadłych i wykonaniu rzutów w tym nowym układzie. Odbywa się to zazwyczaj przez dodanie rzutni prostopadłej do co najmniej jednej z dwóch rzutni poprzednich. Transformację stosuje się, gdy zachodzi potrzeba przedstawienia tworu przestrzennego w rzucie innym, niż rzuty już istniejące, najczęściej dla otrzymania mniej skomplikowanych rzutów lub uzyskania charakterystycznego (równoległego, prostopadłego) ustawienia pewnych fragmentów przedmiotu względem rzutni. Przedstawione w poprzednim rozdziale wyznaczenie trzeciego, bocznego rzutu wielościanu jest szczególnym przypadkiem transformacji rzutu.

1. Transformacja rzutu punktu

Zadanie:

Wyznaczyć trzeci rzut punktu A (A^III) na rzutnię π₃ prostopadłą do rzutni poziomej π₁, a następnie znaleźć czwarty rzut punktu (A^IV) na rzutnię π₄ prostopadłą do rzutni π₃ (rys. 3.1, 3.2). Położenie dodatkowych rzutni - dowolne.

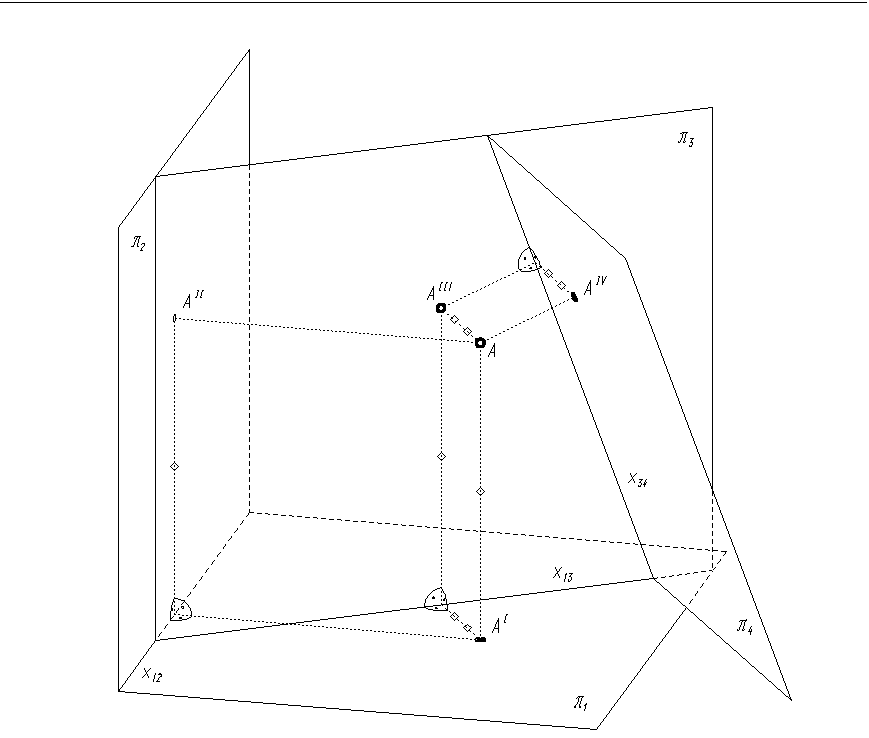
Rys. 3.1

Rozwiązanie zadania:

1. Prowadzimy odnoszącą prostopadle do osi rzutów x₁₃ (krawędzi przecięcia rzutni π₁ i π₃) przechodzącą przez poziomy rzut punktu A (A^I) (rys. 3.2).

2. Na odnoszącej, zazwyczaj po przeciwnej niż punkt A^I stronie osi x₁₃, odkładamy odcinek równy odległości punktu A^II od osi x₁₂, równy również odległości punktu A od rzutni π₁ (odcinki oznaczone na rysunkach 3.1 i 3.2 jednym rombem). W miejscu przecięcia łuku z odnoszącą zaznaczamy punkt A^III.

3. W analogiczny sposób wyznaczamy rzut punktu A na rzutnię π₄ prostopadłą do rzutni π₃ (punkt A^IV). Leży on na odnoszącej przechodzącej przez punkt A^III i prostopadłej do osi rzutów x₃₄ (krawędzi przecięcia rzutni π₃ i π₄), w odległości równej odległości punktu A^I od osi rzutów x₁₃, równej odległości punktu A od rzutni π₃ (odcinki oznaczone dwoma rombami na rysunkach 3.1 i 3.2).

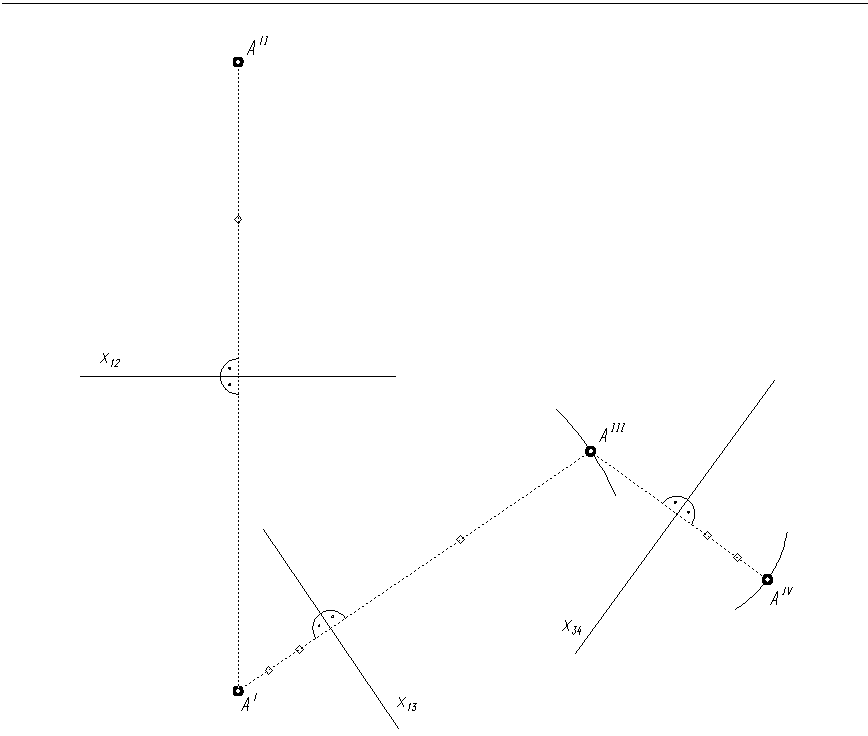
Rys. 3.2

2. Przekrój wielościanu płaszczyzną ogólną

Zadanie:

Ostrosłup ABCW przecięto płaszczyzną α przechodzącą przez punkt M i prostą m. Należy wykreślić rzuty bryły powstałej po przecięciu i odrzuceniu części znajdującej się nad płaszczyzną tnącą oraz wyznaczyć wielkość rzeczywistą przekroju (rys. 3.3, 3.4).

Przekrój bryły, podobnie jak przekrój figury płaskiej, najwygodniej jest wykreślić, jeżeli płaszczyzna tnąca jest płaszczyzną rzutującą, czyli prostopadłą do jednej z rzutni. Wówczas jednym z jej rzutów jest linia prosta, a wyznaczenie punktów przebicia płaszczyzny przez krawędzie bryły jest bardzo łatwe (porównaj: Przykład 1.3). W naszym przypadku płaszczyzna tnąca jest płaszczyzną ogólną, ale można wprowadzić taki nowy układ rzutni, w którym trzeci rzut płaszczyzny będzie prostą.

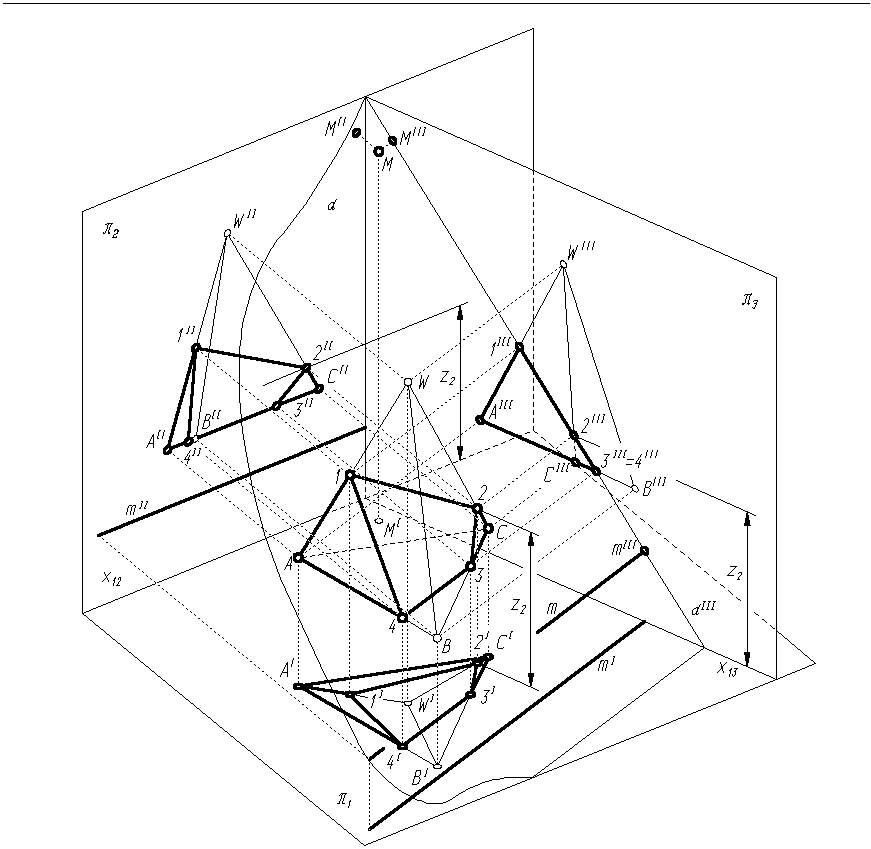
Rys. 3.3

Rozwiązanie zadania:

1. Wprowadzamy trzecią rzutnię π₃ prostopadłą do płaszczyzny α i rzutni poziomej π₁. Zgodnie z warunkiem prostopadłości płaszczyzn, rzutnia π₃ będzie prostopadła do płaszczyzny α, jeżeli będzie prostopadła do jednej z prostych leżących w tej płaszczyźnie. Dodatkowo, aby trzecia rzutnia była prostopadła do rzutni poziomej, prostą tą musi być prosta pozioma. W rozpatrywanym przypadku prostą taką jest prosta m, wyznaczająca wraz z punktem M płaszczyznę α (w ogólnym przypadku należałoby najpierw wykreślić dowolną prostą poziomą leżącą w płaszczyźnie tnącej, patrz: Przykład 1.2). Wprowadzenie trzeciej rzutni polega na narysowaniu w dowolnym miejscu rysunku osi rzutów x₁₃, prostopadłej do poziomego rzutu prostej poziomej m (m^I) (rys. 3.4).

2. Kreślimy trzeci rzut ostrosłupa ABCW oraz elementów wyznaczających płaszczyznę tnącą. Trzecim rzutem prostej m, prostopadłej do rzutni jest punkt m^III, a prosta łącząca punkty M^III i m^III jest rzutem płaszczyzny α na π₃ (α^III).

3. Wyznaczamy rzuty wierzchołków przekroju. Są nimi punkty przecięcia prostej α^III z rzutami krawędzi ostrosłupa: 1^III, 2^III i 3^III.

4. Znajdujemy rzut poziomy i rzut pionowy punktu 1 przez bezpośrednie odrzutowanie punktu 1^III na odcinek W^IA^I, a następnie na W^IIA^II.

5. W analogiczny sposób otrzymujemy brakujące rzuty punktu 2. Większą dokładność rozwiązania uzyskamy jednak, wyznaczając najpierw rzut pionowy punktu 2 (2^II). Odmierzamy wówczas odległość punktu 2^III od osi x₁₃ (odległość punktu 2 od rzutni poziomej, z₂) i kreślimy prostą równoległą do osi x₁₂ aż do przecięcia z odcinkiem W^IIC^II (rys. 3.4). Rzut poziomy 2^I znajdujemy odrzutowując punkt 2^II na odcinek W^IC^I (w taki sam sposób możemy zresztą wyznaczyć rzuty punktu 1).

6. Wyznaczamy rzuty punktów 3 i 4, postępując jak w przypadku punktu 1.

7. Znajdujemy wielkość rzeczywistą przekroju, wprowadzając czwartą rzutnię π₄ prostopadłą do rzutni π₃ i równoległą do płaszczyzny przekroju α (rys. 3.4). W tym celu kreślimy oś rzutów x₃₄ równolegle do α^III. Po odrzutowaniu punktów 1^III, 2 ^III, 3 ^III i 4 ^III, otrzymamy czworokąt 1^IV2^IV3^IV4^IV przystający do 1234.

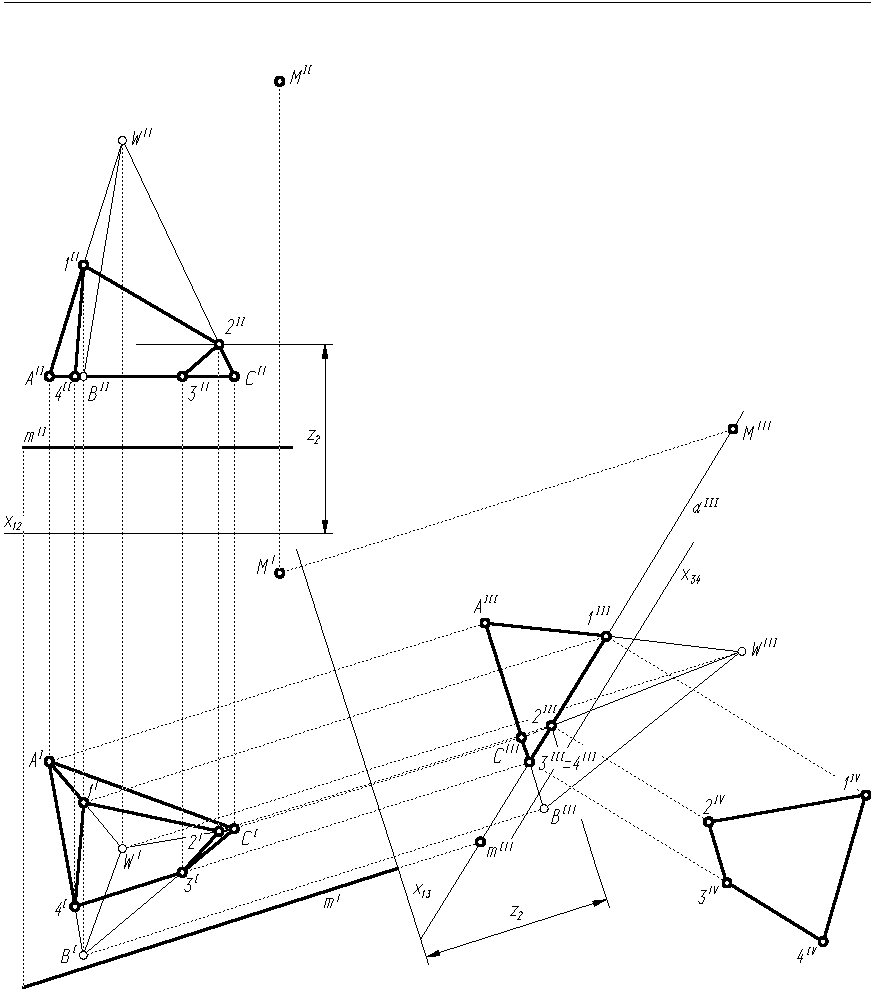
Rys. 3.4

3. Wielościan stojący na płaszczyźnie ogólnej

Zadanie:

Zbudować ostrosłup prawidłowy o podstawie kwadratu, ABCDW, którego podstawa leży w płaszczyźnie ogólnej α wyznaczonej przez punkty K, M, L. Dane są rzuty punktów K, M, L, długość krawędzi podstawy a, oraz wysokość ostrosłupa h (odcinek WS). Jedna z krawędzi podstawy ma być równoległa do rzutni poziomej (rys. 3.5, 3.6).

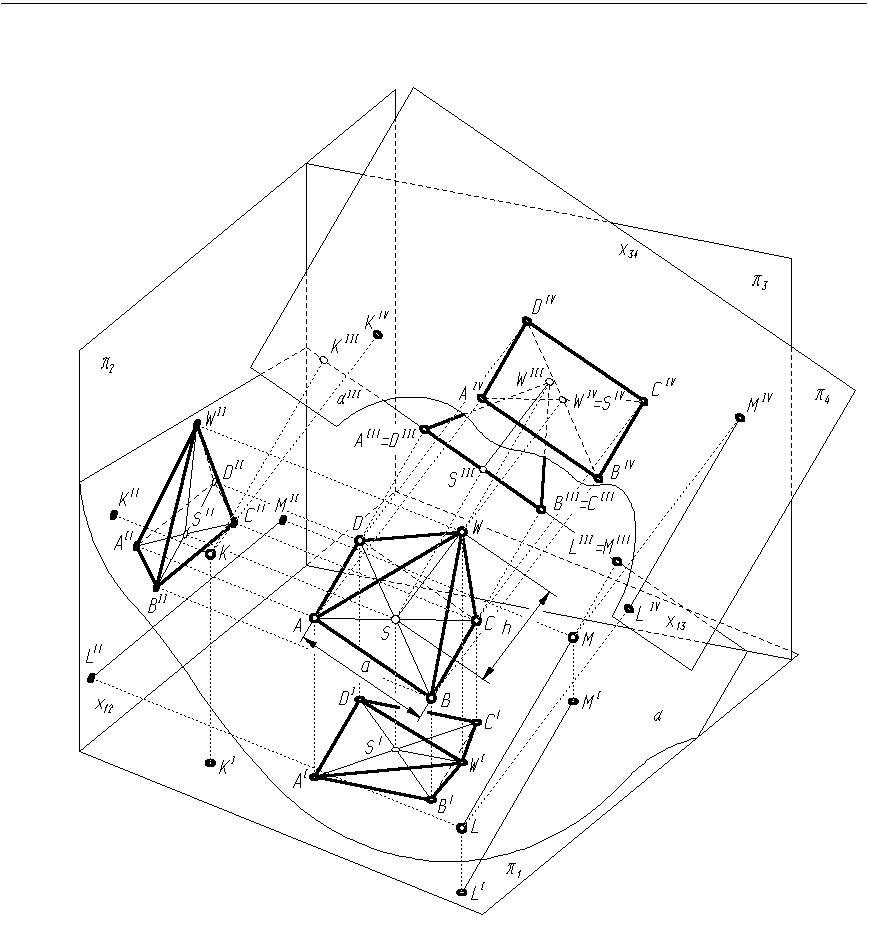
Rys. 3.5

Rozwiązanie zadania:

1. Wprowadzamy rzutnię π₃ prostopadłą do płaszczyzny α i rzutni poziomej π₁. W tym celu na płaszczyźnie α musimy wykreślić lub odnaleźć prostą poziomą. W rozpatrywanym przypadku taką prostą jest prosta przechodząca przez punkty L i M. W dowolnym miejscu rysunku rysujemy oś rzutów x₁₃, prostopadłą do poziomego rzutu prostej poziomej LM.

2. Znajdujemy trzecie rzuty punktów wyznaczających płaszczyznę podstawy ostrosłupa: K^III, L^III i M^III. Trzecie rzuty punktów L i M jednoczą się, a trzecim rzutem płaszczyzny α (α^III) jest prosta przechodząca przez punkty: K^III oraz L^III = M^III.

3. Wprowadzamy rzutnię π₄ równoległą do płaszczyzny α i prostopadłą do rzutni π₃, kreśląc w dowolnej odległości oś rzutów x₃₄ równolegle do α^III.

4. Znajdujemy czwarte rzuty punktów wyznaczających płaszczyznę: K^IV, L^IV i M^IV. Odcinek L^IVM^IV określa kierunek czwartego rzutu prostej równoległej do rzutni poziomej.

5. Wykreślamy czwarty rzut krawędzi podstawy ostrosłupa, odcinek B^IVC^IV. Odcinek ten, o długości a, rysujemy w dowolnym miejscu na prawo od osi rzutów x₃₄, równolegle do odcinka L^IVM^IV.

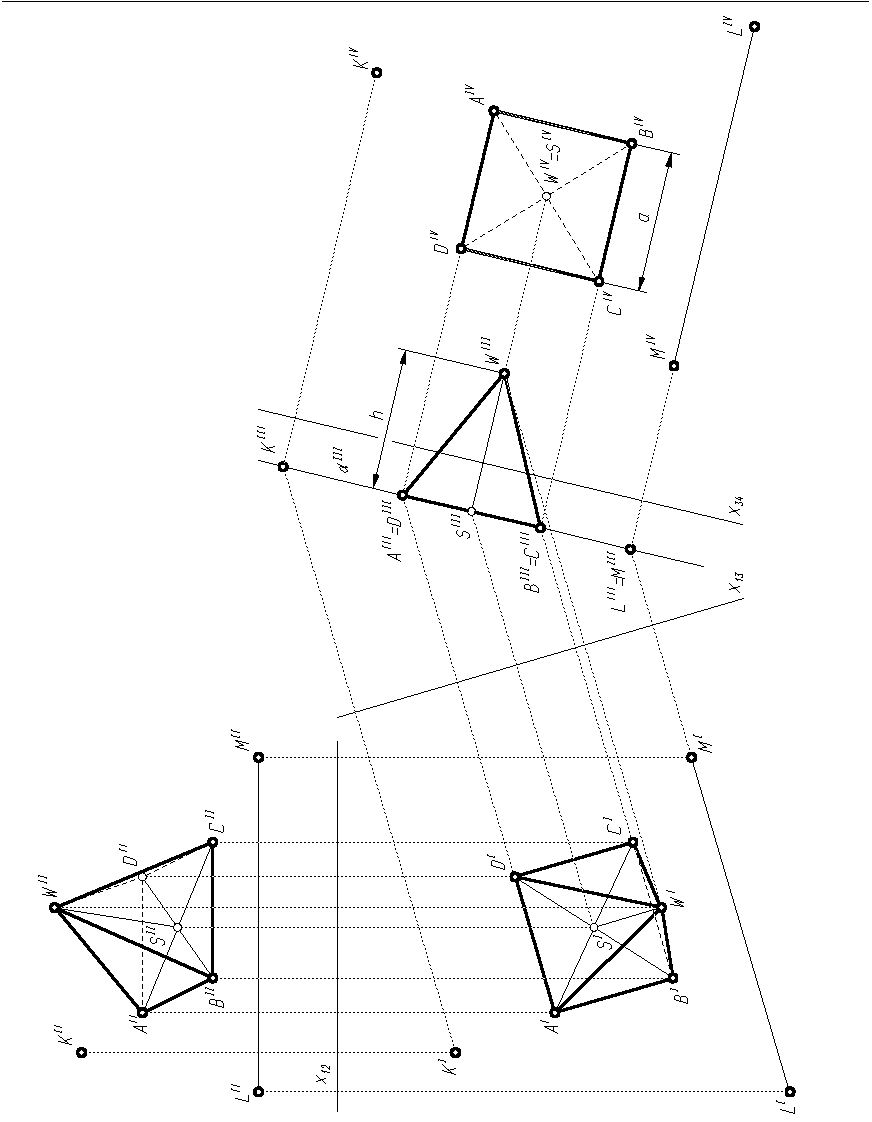
Rys. 3.6

6. Budujemy kwadrat A^IVB^IVC^IVD^IV o długości boków równej a.

7. Kreślimy przekątne kwadratu i w punkcie ich przecięcia znajdujemy czwarty rzut punktu będącego spadkiem wysokości ostrosłupa S^IV. Rzut ten jednoczy się z czwartym rzutem wierzchołka ostrosłupa, punktem W^IV.

8. Wykreślamy krawędzie boczne ostrosłupa: WA, WB, WC i WD. Są one zasłonięte przez podstawę ostrosłupa, więc czwarte ich rzuty rysujemy linią kreskową.

9. Znajdujemy trzecie rzuty wierzchołków podstawy (A^III, B^III, C^III i D^III) oraz punktu S (S^III). Leżą one na trzecim rzucie płaszczyzny α, prostej α^III, przy czym rzuty punktów A i D oraz B i C się jednoczą.

10. Wyznaczamy trzeci rzut wysokości ostrosłupa, odcinek W^IIIS^III o długości równej h. Wysokość WS jest prostopadła do płaszczyzny podstawy, więc jej trzeci rzut jest prostopadły do α^III.

11. Rysujemy trzeci rzut ostrosłupa, łącząc odcinkami narysowane wcześniej trzecie rzuty punktów.

12. Wykreślamy poziomy, a następnie pionowy rzut ostrosłupa ABCDW. W obydwu rzutach linią kreskową rysujemy te krawędzie, które są niewidoczne. W naszym przypadku, w rzucie poziomym niewidoczna jest krawędź BC, a w rzucie pionowym krawędzie: AD, DC i WD.

4. Rysunek części maszynowej z rzutem ukośnym

Zadanie:

Wykorzystując transformację rzutu wykonać rysunek techniczny (z uwzględnieniem typów i grubości linii rysunkowych, kreskowania i oznaczeń) części maszynowej, której przedstawienie wymaga zastosowania rzutu ukośnego: widoku pomocniczego lub cząstkowego, przekroju, albo kładu przekroju (rys. 3.7, 3.8, 3.9, 3.10).

Rozwiązanie zadania:

1. Kolejne etapy wykonywania zadania przedstawiono na rysunkach a, b, c (dla każdego z przykładów). W danych (rysunki a) pokazano widok z przodu i widok z góry części maszynowej oraz zaznaczono płaszczyzny przekrojów i kierunki widoków.

2. Wykreślanie przekrojów walca omówiono w rozdziale 4.

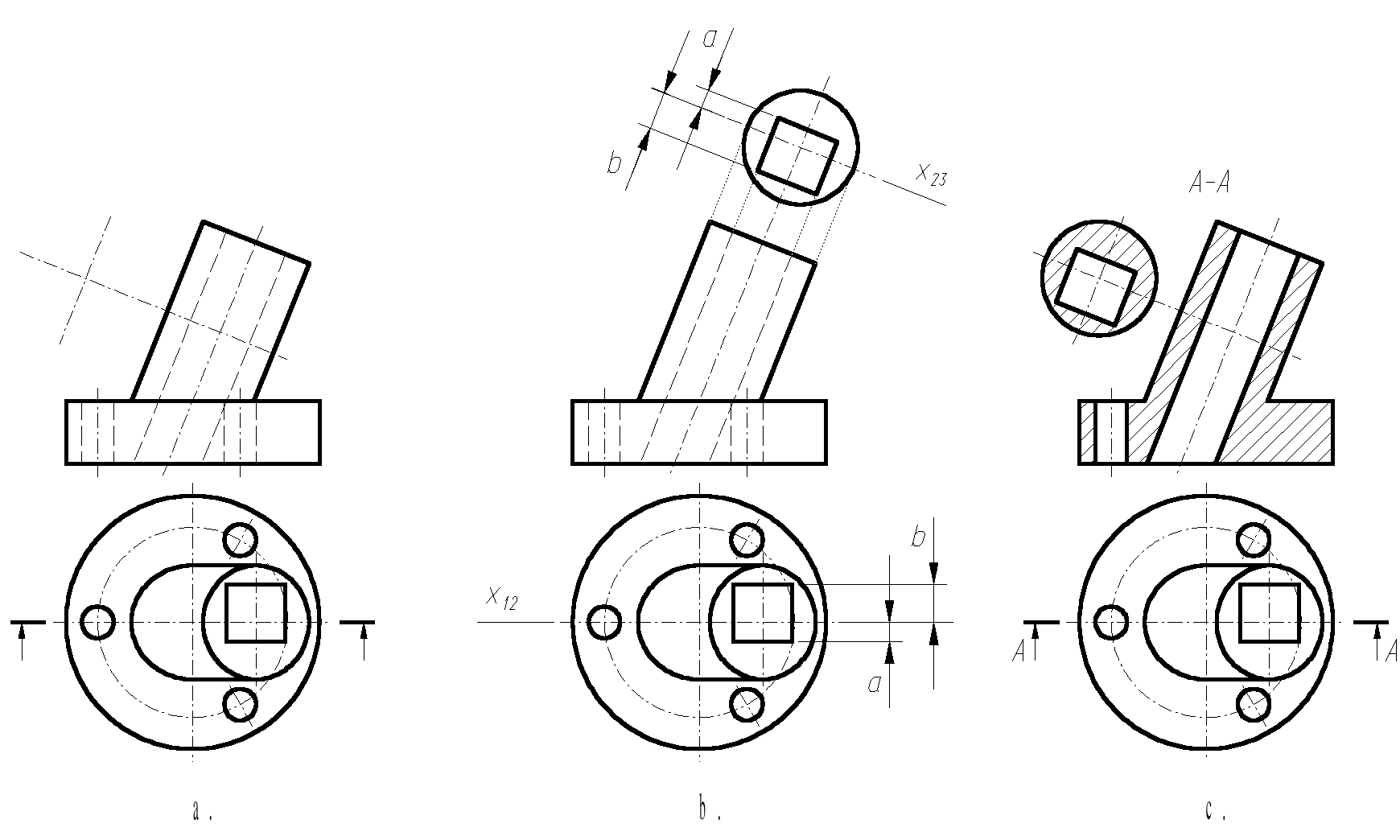
Rys. 3.7

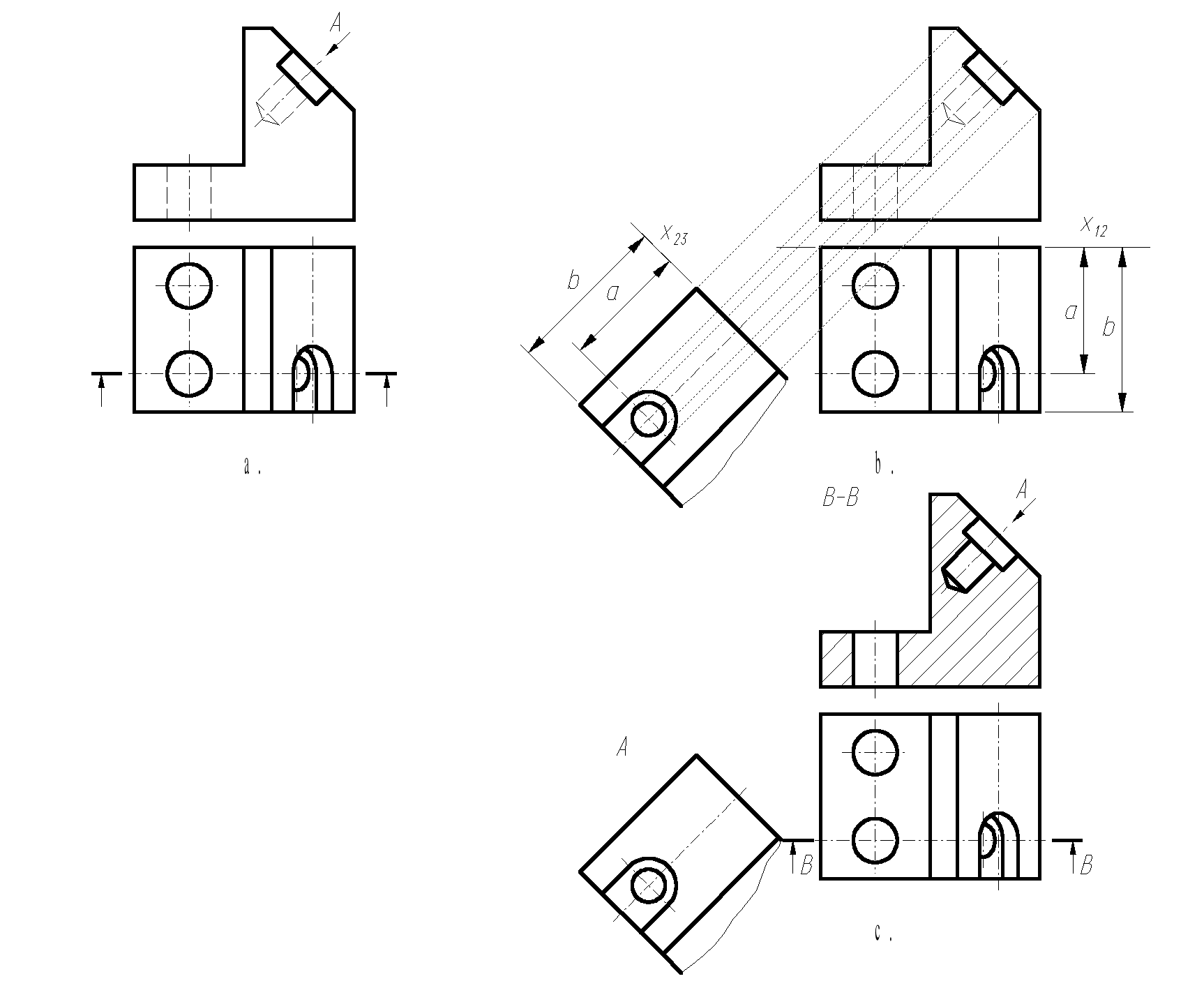
Rys. 3.8

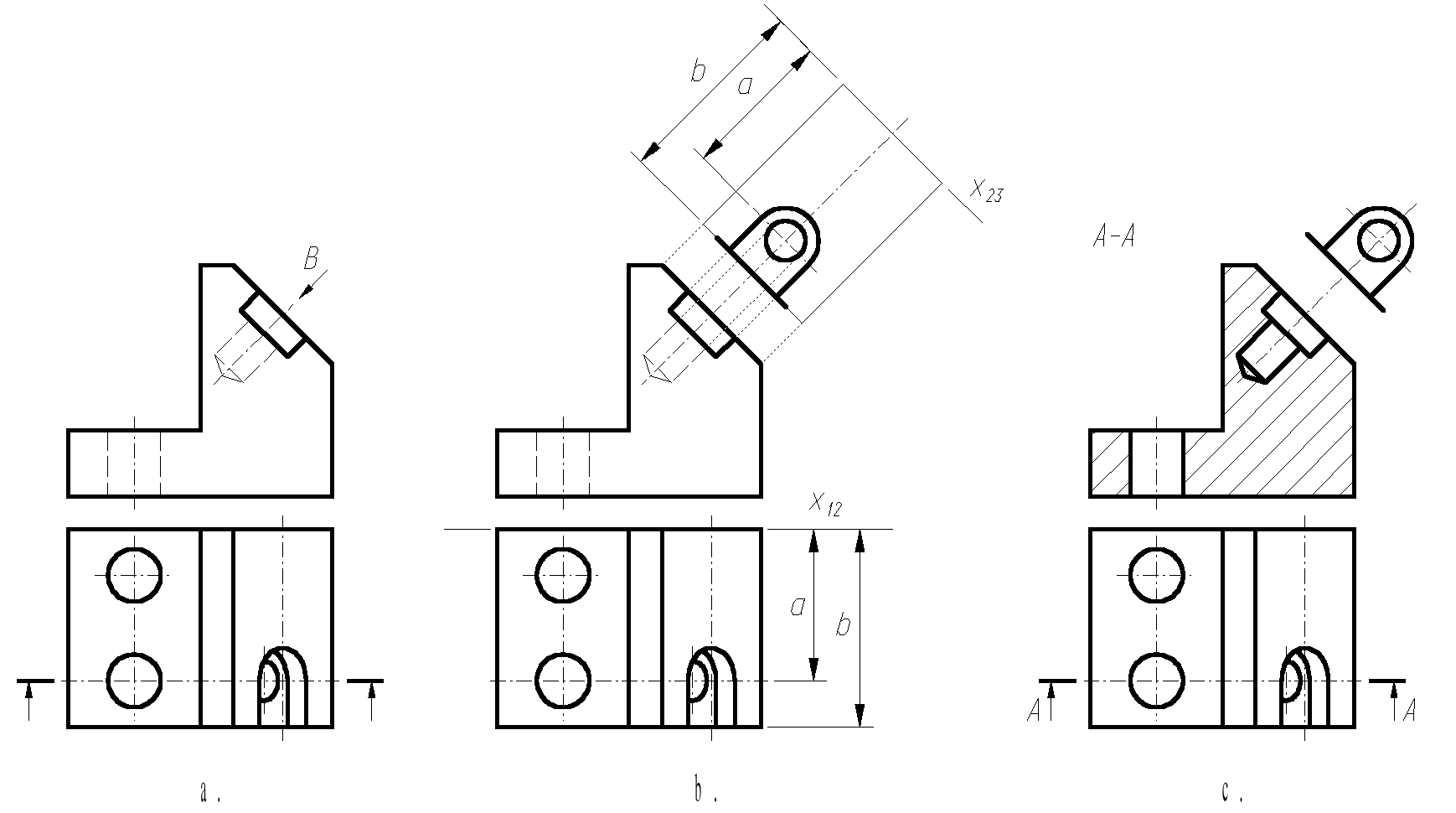
Rys. 3.9

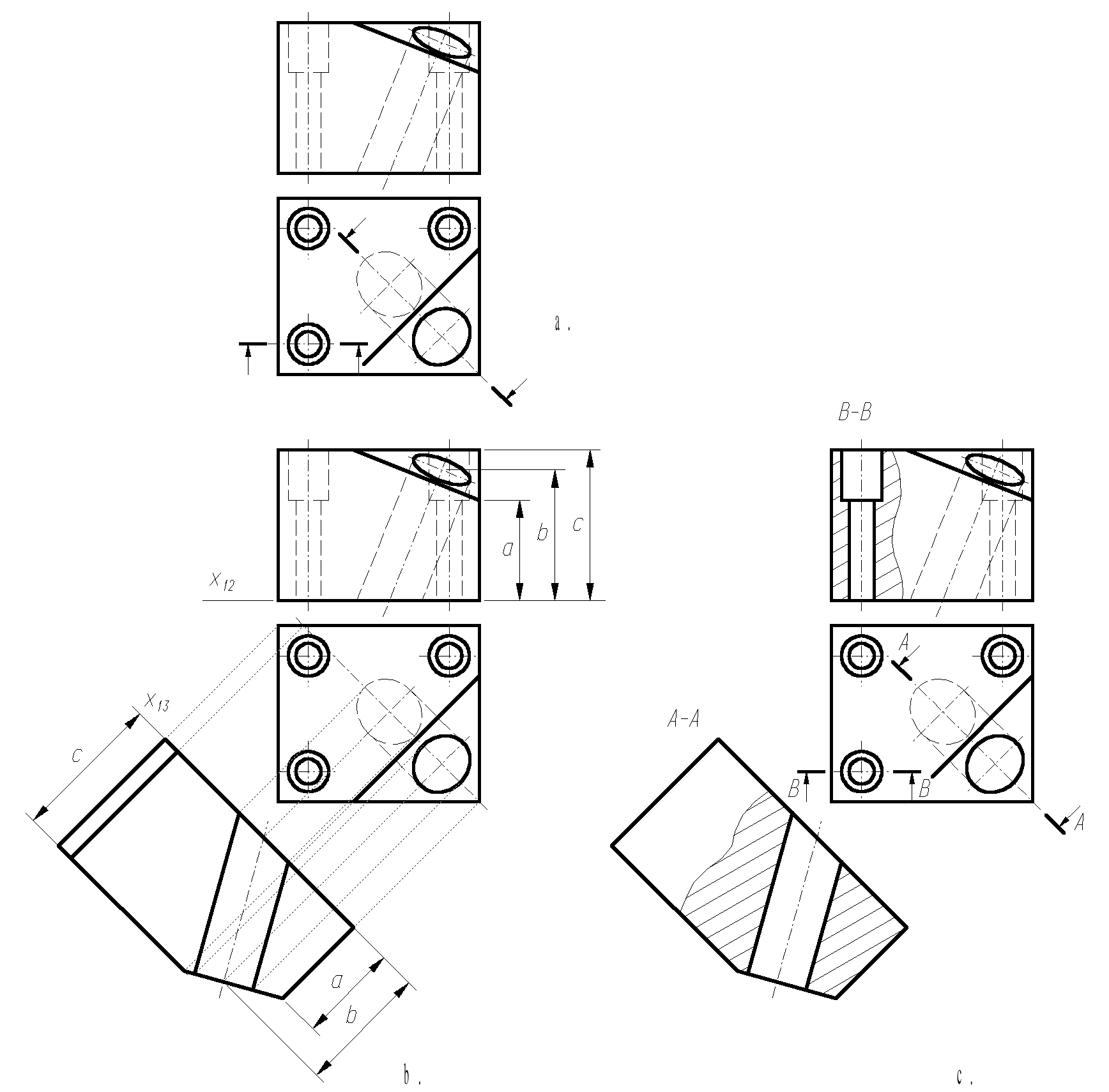
Rys. 3.10

14

Politechnika Łódzka, Katedra Konstrukcji Precyzyjnych

13

Materiały pomocnicze do Geometrii Wykreślnej

---