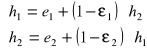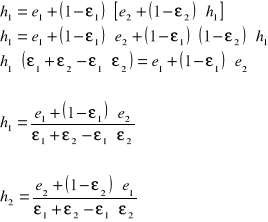Dwie powierzchnie obejmujące się.

A, a - powierzchnie

c_c - stała promieniowania

ε_d - emisyjność dużej powierzchni

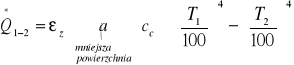
T₁ > T₂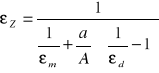

Jeżeli a ≈ A to:

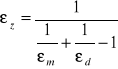
gdy a << A to:

EKRANY

Strumień ciepła z jednej powierzchni na ekran jest równy strumieniowi ciepła z ekranu na drugą powierzchnię. Energia ekranu nie zmienia się.

t_ot Q_k Q_r

γ_śc^h

γ_śc^r

Q_k - strumień konwekcyjny

Q_r - strumień radiacyjny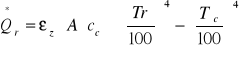

α_k - współczynnik przenikania ciepła wynikający z promieniowania radiacyjnego

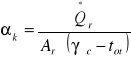
Całkowity współczynnik przejmowania ciepła wyraz się wzorem:

α = α_k + α_r

α_k - współczynnik konwekcji

α_r - współczynnik radiacji

PRZYKŁAD

t_t = 20°C

t_pow = ?

Q_k γ_śc = 15°C

Q_r

a

ε_c = 0,9 α_k = 4 W/m²K

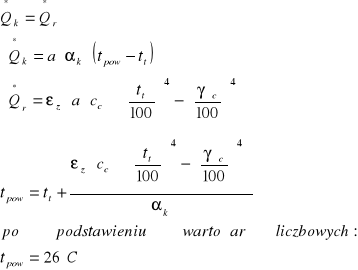
INTENSYWNOŚĆ PROMIENIOWANIA

Powierzchnia emituje emisję własną. Ile promieniuje w danym kierunku?

półprzestrzeń

E, e

I_n

dΩ

β I_β

dA

Intensywność promieniowania I_β:

Prawo Lamberta:

WSPÓŁCZYNNIK KONFIGURACJI

n₁ 2

dA₂

β₂

r

n₂

β₁

dA₁

1

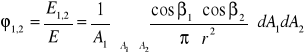
E_∩ - emisja wysyłana do całej półprzestrzeni

E_1,2 - część emisji, która pada na powierzchnię 2

Policzyć strumienie ciepła przekazywanego między tymi powierzchniami:

ε=0, T=0

ε=0, T=0

ε




=0, T=0

ε=0, T=0

Jasność powierzchni „i“:

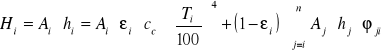
Strumień promieniowania powierzchni ”i”:

DWIE POWIERZCHNIE RÓWNOLEGŁE NIESKOŃCZENIE DUŻE

T₁, ε₁ T₂, ε₂

Jeśli T₁ > T₂ to

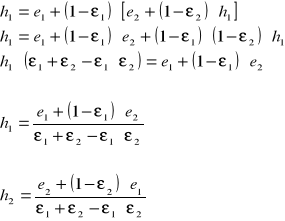
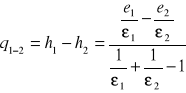
Z prawa S-B:

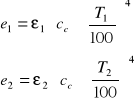
więc:

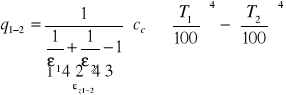
DZIAŁANIE EKRANÓW

1 2 n

ε₁, T₁ ε₂, T₂

T_e1 T_e2 T_en

q_1-e

q_e1-e2

q_e2-en

q_en-2

Przegrody nieprzezroczyste (ekrany)

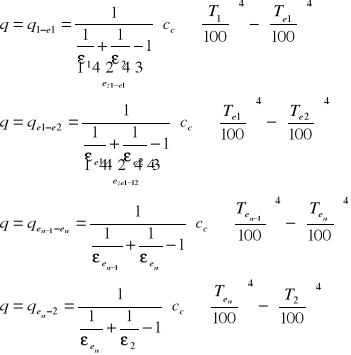
przekształcając otrzymamy trzy równania:

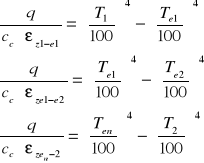
z których wyznaczymy strumień przekazywanego ciepła „q” :

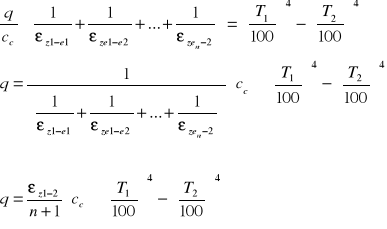
ε₁ = ε_e = ... = ε₂

PROMIENIOWNIE GAZÓW

e_λ

widmo promieniowania ciała doskonale czarnego

g

e

rz

λ

Promieniowanie gazów jest nieciągłe. Gazy trójatomowe; dwutlenek węgla, para wodna promieniują najbardziej.

Gazy promieniują całkowicie (całą objętością). Promieniowanie gazów nie jest proporcjonalne do potęgi 4 , ale do 3. Dla ułatwienia korzystamy z tego samego wzoru:

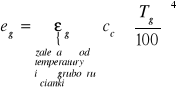
ε_g = f (T_g, ρl)

Jeżeli bryłę gazową ograniczymy ścianką to strumień ciepła między gazem a ścianką wynosi:

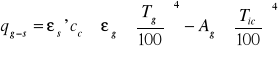
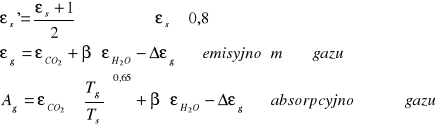
ε
_CO2

ε
_H2O ρl

T

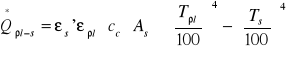
Temperaturę płomienia wylicza się z średniej temperatury w całym palenisku.

T₂

ε₂ a

T₁ ε₁

A

Cała jasność powierzchni „a” promieniuje na powierzchnię „A” , ale tylko część jest pochłaniana

T₁ a

ε_m

Q_1-e

Q_e-2

A_e ε_e

A T₂

ε_d

1

2

3

4

i

n

Dla układu otwartego powierzchni, przerwy zastępujemy powierzchniami doskonale czarnymi (ε = 0, T = 0)