Państwowa Wyższa Szkoła Zawodowa W Elblągu Instytut Informatyki Stosowanej Laboratorium Architektury Systemów Komputerowych
Grupa dziekańska: Grupa laboratoryjna:	Tytuł ćwiczenia: Układy kombinacyjne
Skład grupy: 1.Krzysztof Borzęcki 2.Remigiusz Jasiński 3.	Data wykonania:16.10.2010 Data oddania:06.11.2010
		Ocena:

1. Układy funkcji Boole'a

Dany jest układ zapisany w postaci funkcji Boole'a: Y=A'*B*C+A*B'*C+A*B*C'+A*B*B+A'*B'*C

gdzie * oznacza iloczyn logiczny (AND), + sumę logiczną (OR) a ' negację (NOT).

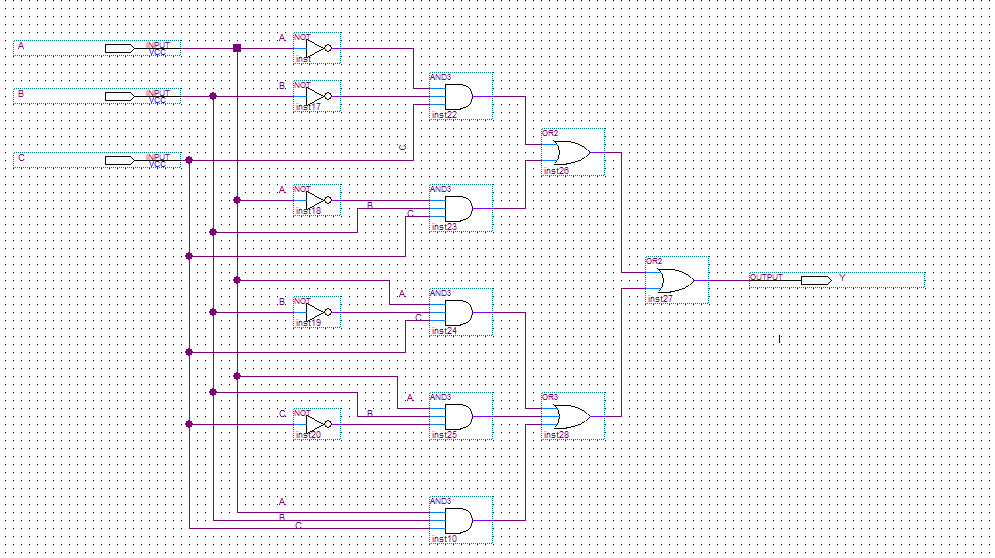
Tworzymy układ prezentujący powyższą funkcję.

Rysunek 1. Układ spełniający wyżej podaną funkcję Boole'a.

WEJŚCIA
A	B	C
0	0	0
1	0	0
0	1	0
1	1	0
0	0	1
1	0	1
0	1	1
1	1	1

Tabela 1. Dane wejściowe wykorzystane w symulacjach.

Rysunek 2. Dane wejściowe w formie pliku wsadowego do symulacji.

Rysunek 3. Wykres symulacji typu timing.

Rysunek 4. Wykres symulacji typu functional.

Optymalizacja układu z wykorzystaniem tablicy Karnaugha.

	0	1
00	0	0
01	1	0
11	1	1
10	1	0

Tablica 2. Tablica Karnaugha.

Y(A,B,C)=A'*B*C'+A*B*C'+A*B*C+A*B'*C'

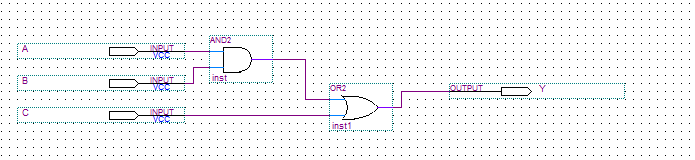
Rysunek 5. Układ po optymalizacji.

Przeprowadzona symulacja wykazała, że uzyskiwane wyniki są takie same jak przy rozbudowanym układzie.

UKŁAD ALARMOWY.

M	W	D	S
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Tabela 3. Układ alarmowy, 1 w kolumnie S oznacza włączenie się alarmu.

Jak wykazuje tablica uruchomienie alarmu następuje w sytuacjach które można wyrazić następującą funkcją Boole'a: S(M,V,D)=M*V'*D+M*V*D'+M*V*D

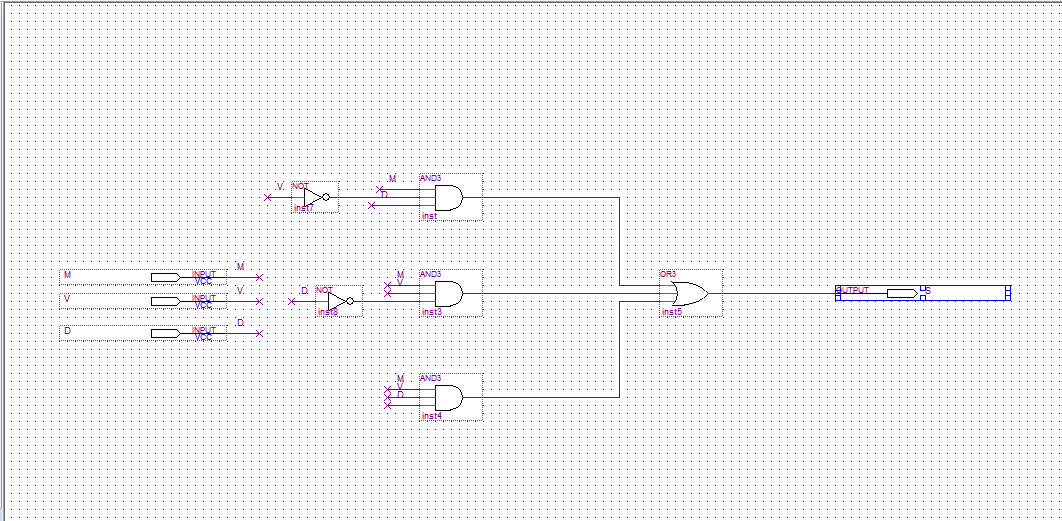
Rysunek 6. Układ alarmowy.

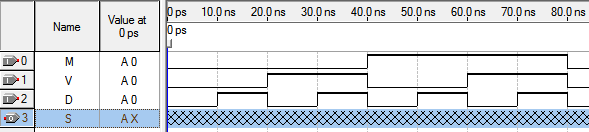
Rysunek 7. Dane wejściowe.

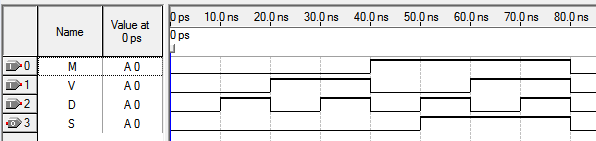
Rysunek 8. Dane wyjściowe po symulacji typu functional.

Jak można zauważyć w tablicy prawdy układu uruchomienie syreny następuje gdy zmienne V i D dają na wyjściu 1 oraz M jest równe 1. Jest to wynik działania bramki OR. Wobec powyższego zoptymalizowany układ będzie zawierał dwie bramki OR.

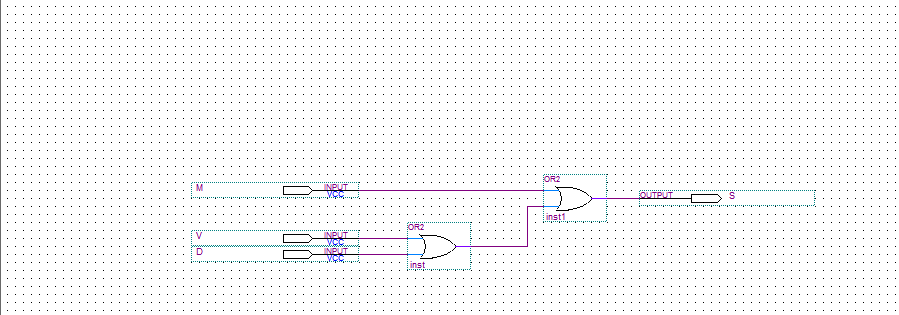
Rysunek 9. Zoptymalizowany układ alarmowy.

Państwowa Wyższa Szkoła Zawodowa W Elblągu, Instytut Informatyki Stosowanej

Laboratorium Architektury Systemów Komputerowych

str. 4

---