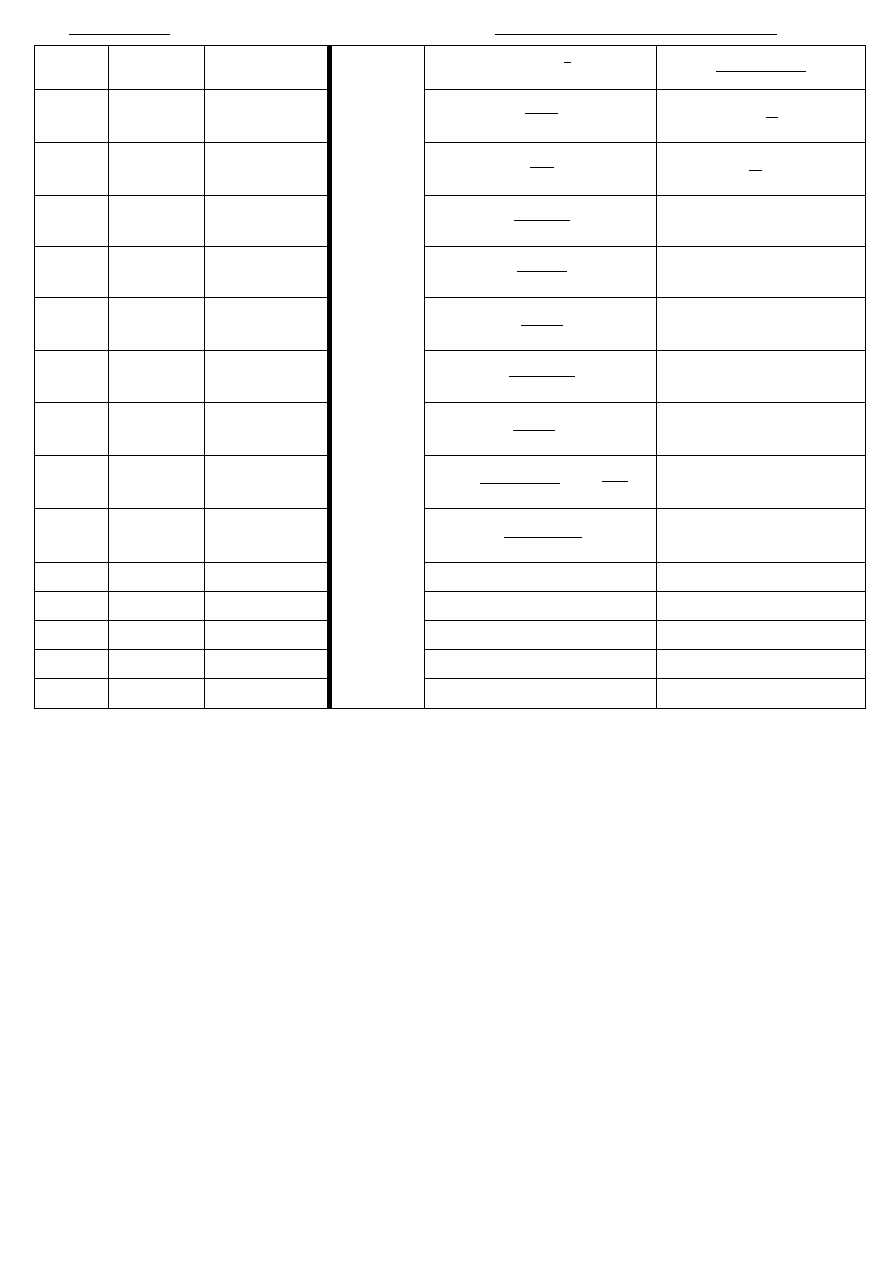
POCHODNE

GRANICE POD. WYRAŻEŃ ( x-_>0)

Funkcja Pochodna

Uwagi

lim x1

1
x

=e

x-->(+/-)∞

c

0

c<=>R

lim

sinx

x

= 1

lim 1

1

x



x

= e

x

a

ax

a-1

a<=>R

lim

tgx

x

= 1

lim 1 a

x



x

=  e

a

a

x

a

x

lna

a>0, x<=>R

lim

arcsinx

x

= 1

e

x

ex

x<=>R

lim

arctgx

x

= 1

log

a

x

1

/

xlna

0<a≠1, x>0

lim e

x

−

1

x

= 1

lnx

1

/

x

x>0

lim

ln x 1

x

= 1

sinx

cosx

x<=>R

lim a

x

−

1

x

= lna

cosx

-sinx

x<=>R

lim

log

a



1x 

x

= 

1

lna

tgx

1

/

cos

2

x

x≠90

Lim



x1

a

−

1

x

= a 

ctgx

-(

1

/

sin

2

x

)

x≠180

arcsinx

1

/√

1-x

2

x<=>(-1;1)

arccosx

-(1

/√

1-x

2)

x<=>(-1;1)

arctg

1

/

1+x

2

x<=>R

arcctg

-(

1

/

1+x

2

)

x<=>R

<=> - należy.

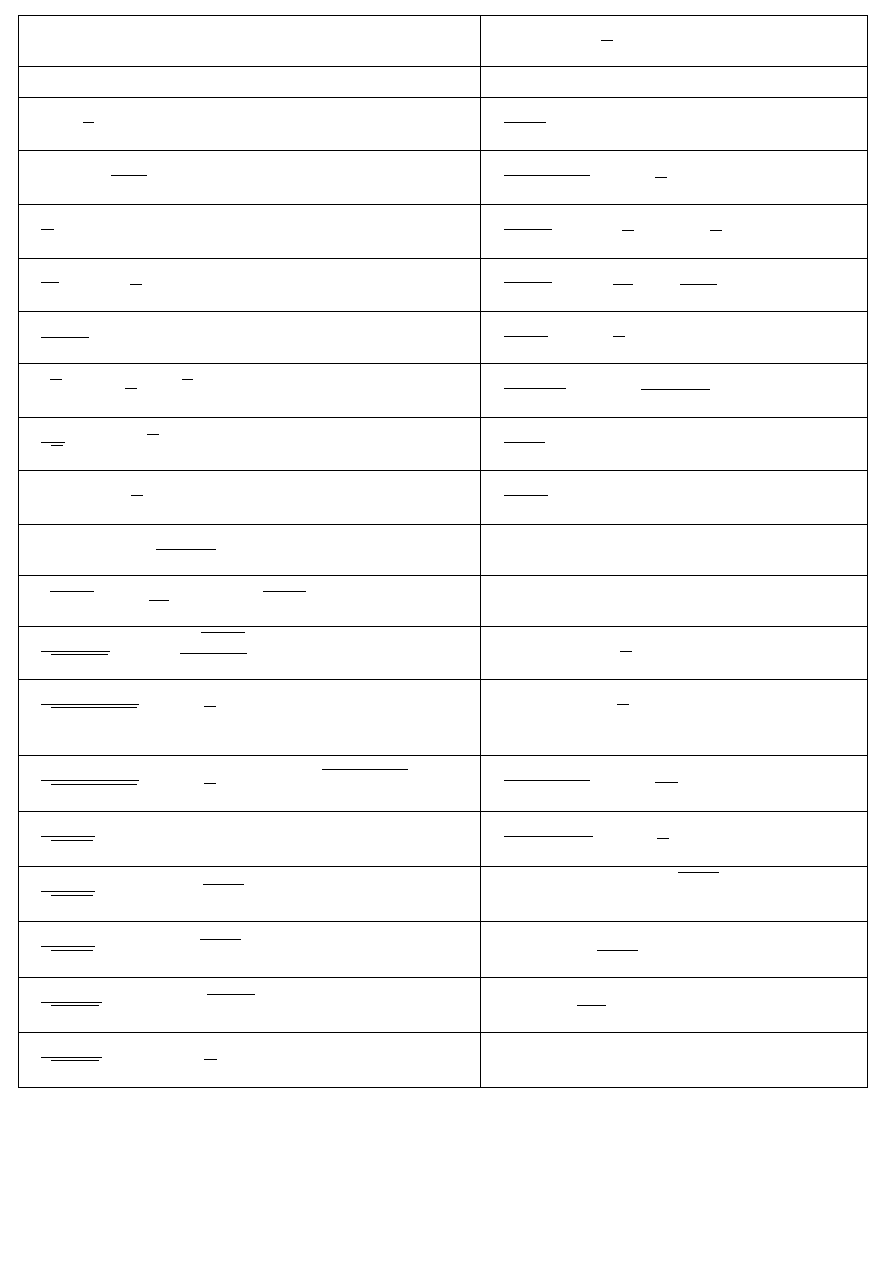
∫ 0dx=C

∫ e

axb

dx = 

1
a

e

axb

+C,  a≠0

∫ dx=x+C

∫ 

e

x

=  e

x

+C

∫ xdx=

1
2

x

2

+C

∫

dx

1x

2

dx = arctanx +C

∫ x

n

dx=

1

n1

x

n1

+C, n≠0

∫

dx

1 axb

2

dx = 

1
a

arctan (ax+b)+C,  a≠0

∫

1

x

dx=ln|x|+C

∫

dx

a

2



x

2

dx =  

1
a

arctan 

x

a

+C,  a≠0

∫

1

x

2

dx = -

1

x

+C

∫

dx

a

2

−

x

2

dx =

1

2a

ln

∣

ax
a−x

∣

+C, a>0 i |x|≠0

∫

f '  x 

f  x 

dx = ln|f(x)|+C

∫

dx

axb

dx = 

1
a

ln|ax+b|+C, a≠0

∫



x dx = 

2
3

x



x +C

∫

dx



ax b

2

dx = - 

1

a axb 

+C

∫

dx



x

dx = 2



x +C

∫

1

sin

2

x

dx = -cotx +C

∫ (ax+b)dx = 

a
2

x

2

+bx+C

∫

1

cos

2

x

dx = tgx +C

∫ axb

n

dx=

1

a n1



axb

n1

+C, a≠0, n≠-1 

∫ sinxdx = -cosx +C

∫



axb dx=

2

3a



axb



axb +C, a≠0

∫ cosxdx = sinx +C

∫

1





axb

dx = -

2



axb

a

+C, a≠0

∫ sin(ax+b)dx = -

1
a

cos(ax+b) +C, a≠0

∫

dx



1− axb

2

dx = 

1
a

arcsin ax bC , a≠0

∫ cos(ax+b)dx = 

1
a

sin(ax+b) +C, a≠0

∫

dx



1 axb

2

dx = 

1
a

ln axb





axb

2



1 , a≠0

∫

1

sin

2



axb

dx = 

−

1

a

cot(ax+b) +C , a≠0

∫

1



1−x

2

dx =arcsinx+C, a≠0

∫

1

cos

2



axb

dx = 

1
a

tg(ax+b) +C , a≠0

∫

1



1x

2

dx =ln(x+



x

2



1 ) +C

∫ arctgxdx= xarctgx - ln



x

2



1 +C

∫

1



x

2

−

1

dx =ln|x+



x

2

−

1

|+C, |x|>1

∫

m

axb

dx= m

axb

alnm

+C,  m≠1 i  a≠0

∫

1



x

2

−

a

2

dx =ln|x+



x

2

−

a

2

|+C,  a≠0

∫ m

x

dx= m

x

lnm

+C,  m≠1 i m>0

∫

1



a

2

−

x

2

dx =arcsin

x

a

+C,  a>00

∫lnxdx= xlnx -c +C