CAŁKI WIELOKROTNE, KRZYWOLINIOWE I POWIERZCHOWNE.

Całka podwójna i jej obliczanie przez dwukrotne całkowanie.

Niech
będzie funkcją ciągłą w pewnym domkniętym obszarze
na płaszczyźnie. Podzielmy obszar
w dowolny sposób na
obszarów częściowych o polach
, wybierzmy w każdym z nich po jednym (dowolnym zresztą) punkcie
obliczmy odpowiadające tym punktom wartości funkcji i utwórzmy sumę:

nazywaną sumą całkowitą funkcji
po obszarze
.

Oczywiście, wartość sumy całkowitej zależy i od sposobu podziału obszaru
na n obszarów składowych i od wyboru punktów
w tych obszarach. Innymi słowy, dla dane funkcji
i dla każdego obszaru domkniętego
, gdzie funkcja
jest określona, można utworzyć nieskończenie wiele różnych sum całkowych.

Jeżeli jednak
rośnie nieograniczenie i największa ze średnic obszarów częściowych dąży przy tym do zera, to wszystkie te sumy całkowite dążą do jednej i tej samej granicy. Granicę tę nazywamy całką podwójną funkcji
po obszarze
i oznaczamy symbolem
.

Całka podwójna ma te same podstawowe własności co zwykła całka oznaczona: obszar całkowania w całce podwójnej można dzielić na części, całka podwójna sumy funkcji jest równa sumie całek poszczególnych składników, czynnik stały wolno wyłączyć przed znak całki podwójnej.

Obliczanie całki podwójnej
sprowadza się do obliczenia jednej lub kilku (w zależności od obszaru) całek iterowych (dwukrotnych) dwukrotnych postaci:

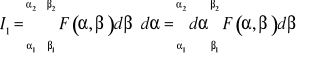
albo

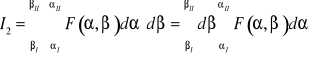
z których każda jest wynikiem kolejnego obliczania dwóch zwykłych całek oznaczonych.

W całce iterowanej
funkcja
jest najpierw całkowana względem
, przy tym
traktuje się jako stałą, a następnie otrzymamy wynik całkuje się względem
.

W całce iterowanej
całkowanie odbywa się w odwrotnej kolejności, najpierw całkujemy względem
, traktując przy tym
jako stałą, a następnie otrzymamy wynik całkuje się względem
.

Z reguły przy pierwszym całkowaniu granice są zmienne i zależą od tej zmiennej, która jest przy tym traktowana jako stała. Natomiast granice przy drugim całkowaniu są zawsze stałe.

Całka podwójna we współrzędnych biegunowych.

Jeżeli obszar całkowania w całce podwójnej jest odniesiony do współrzędnych biegunowych
i jest dzielony na obszary częściowe promieniami
, wychodzącymi z bieguna, i okręgami współśrodkowymi

Zwykle całki podwójne we współrzędnych biegunowych wyrażają się całkami iterowanymi o postaci

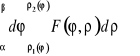
Granice całkowania względem
wyznaczają zakres zmienności
przy stałej, aczkolwiek dowolnej wartości
. Granice całkowania względem
są stałe i przedstawiają odpowiednio najmniejszą i największą spośród wartości
w całym obszarze.

Z reguły, granice całki wewnętrznej (względem
)zależą od
. Obie granice są stałe tylko w tym przypadku, gdy obszar całkowania jest wynikiem kołowym albo różnicą wycinków kołowych o środku w biegunie (początku) układu. Granice całki zewnętrznej (względem
) są zawsze stałe.

Przy zastosowaniu całek podwójnych do zadań z zakresu geometrii i fizyki, zwykle wielkość poszukiwana jest wyrażona pewną całką podwójną odniesioną do współrzędnych prostokątnych, a dopiero potem w wielu przypadkach jest sprowadzana, w celu uproszczenia obliczeń, do współrzędnych biegunowych. Obowiązuje przy tym następująca reguła.

Aby całkę podwójną odniesioną do współrzędnych prostokątnych przekształcić na całkę podwójną we współrzędnych biegunowych, trzeba w wyrażeniu podcałkowym wyrazić współrzędne biegunowe, wg wzorów
,
i zamiast
postawić
.

Obliczanie pół za pomocą całki podwójnej.

Pole S płaskiego obszaru D jest równe całce podwójnej z
, rozciągniętej na obszar D.

We współrzędnych prostokątnych
, więc

a we współrzędnych biegunowych
, więc

Masa, środek ciężkości i moment bezwładności.

Niech dana będzie płaska figura materialna (płytka). Jeśli przez
oznaczamy gęstość powierzchniową masy w punkcie
, to masa
, współrzędne środka ciężkości
i momenty bezwładności płytki względem osi
i
, i względem początku układu dane są wzorami

(
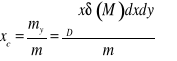
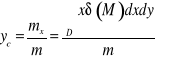
i
- momenty statyczne płytki względem osi
i
; dla płytki jednorodnej
i wzory upraszczają się po wyłączeniu
przed znaki całek)

Dla jednorodnej bryły materialnej w kształcie walca, ograniczonej od góry powierzchnią
i mającej za podstawę obszar D leżący na płaszczyźnie
.

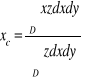
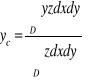
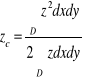
Całka potrójna i jej obliczanie przez trzykrotne całkowanie.

Niech funkcja
będzie określona i ciągła w pewnym domkniętym obszarze
przestrzeni. Podzielmy obszar
na n obszarów częściowych w dowolny sposób. Oznaczmy objętości obszarów częściowych przez
i wybierzmy każdym z nich pewien punkt
. Obliczmy wartość funkcji
w tych punktach i utwórzmy sumę

nazywamy sumą całkowa funkcji
po obszarze
.

Tworząc sumę całkową obszar
można dzielić na obszary częściowe w różny sposób i w różny tez sposób można wybierać w tych
obszarów częściowych po jednym punkcie
. Dla każdej więc funkcji i dla każdego obszaru
można utworzyć dowolnie wiele sum całkowych. Jeśli jednak
rośnie nieograniczenie, a średnia największego z obszarów częściowych dąży przy tym do zera, to wszystkie te sumy całkowite zmierzają do jednej i tej samej granicy. Granicę tę nazywamy całką potrójną funkcji
po obszarze
i oznaczamy symbolem
.

Własności całek potrójnych SA analogiczne do własności całek podwójnych i zwykłych całek oznaczonych: obszar całkowania wolno dzielić na części składowe, całka sumy funkcji jest równa sumie całek poszczególnych składników, czynnik stały wolno wyłączyć przed znaki całki.

Obliczanie całki potrójnej sprowadza się do obliczenia całki trzykrotnie iterowanej, tj. do kolejnego obliczenia trzech zwykłych jednokrotnych całek oznaczonych względem każdej ze zmiennych współrzędnych punktu przestrzeni trójwymiarowej.

Jeśli obszar całkowania jest odniesiony do układu współrzędnych prostokątnych
i jest dzielony na obszary elementarne za pomocą płaszczyzn układu, to objętość obszaru elementarnego wynosi
i całka potrójna ma postać

Jeśli przy tym obszar
ma tę samą własność, że proste poprowadzone przez jego punkty wewnętrzne, równolegle do osi
, przecinają jego granicę tylko w dwóch punktach, to całkę potrójną można obliczyć ze wzoru

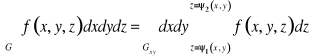
w którym
jest rzutem obszaru
na płaszczyznę
,a
i
są równaniami powierzchni ograniczających obszar
od dołu i od góry.

Wzór ten sprowadza obliczenie całki potrójnej do kolejnego obliczenia zwykłej (jednokrotnej) całki oznaczonej względem zmiennej
, przy czym zmienne
traktuje się jako stałe, i całki potrójnej o zmiennych całkowania
i
, rozpostartej na obszar
leżący w płaszczyźnie
.

Z reguły granice całki wewnętrznej (jednokrotnej) są zmienne. Zależą one od tych dwóch zmiennych, które przy obliczaniu tej całki są traktowane jako stałe. Granice obydwu całek będą stałe tylko wtedy, gdy obszarem całkowania jest walec prosty, o tworzących równoległych do osi
i podstawach leżących na płaszczyznach równoległych do płaszczyzny
.

Zamieniając rolę zmiennych
, y i
we wzorze powyżej, można otrzymać inne analogiczne wzory na obliczanie całki potrójnej za pomocą kolejnego obliczania całki zwykłej i całki podwójnej.

Przy obliczaniu całki potrójnej w podany wyżej sposób, niekiedy, po obliczaniu całki wewnętrznej, warto przed obliczeniem całki podwójnej wprowadzić współrzędne biegunowe. O tym sposobie obliczania całki potrójnej mówimy, że polega on na sprowadzeniu całki do współrzędnych walcowych, zmienne
i
są właśnie współrzędnymi walcowymi punktu
.

Całkę potrójną można też obliczać inaczej: najpierw obliczyć całkę podwójną, o zmiennym obszarze całkowania, a potem całkę jednokrotną.

Obliczanie wielkości za pomocą całki potrójnej.

Objętość, masę, współrzędne środka ciężkości oraz momenty bezwładności bryły, obliczamy wg następujących wzorów:

1. Objętość obszaru przestrzennego
   

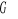
2. Masa bryły materialnej wypełniającej obszar
   

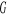
gdzie:
- gęstość objętościowa masy w punkcie
bryły.

3. Współrzędne środka ciężkości
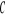
   bryły

gdzie:
i
- momenty statyczne bryły względem płaszczyzny układu, wyrażające się wzorami

Dla bryły jednorodnej
wzory upraszczają się po wyłączeniu
przed znaki całek.

4. Momenty bezwładności bryły względem osi
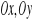
   i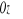
   oraz względem początku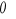
   układu współrzędnych

Całki krzywoliniowe i ich obliczanie, Warunek niezależności od drogi całkowania.

Rozważmy pewną funkcję
ciągłą w każdym punkcie
łuku
. Podzielmy ten łuk w dowolny sposób na
łuków częściowych, częściowych długościach
i wybierzmy na każdym z nich po jednym, dowolnym zresztą, punkcie
. Obliczmy wartość funkcji
w tych punktach i utwórzmy sumę

nazywaną sumą całkowitą funkcji
po łuku
.

Naturalnie, dla każdej danej funkcji
i dla każdego danego łuku
można utworzyć nieskończenie wiele różnych sum całkowitych, dzieląc w różny sposób łuk na
części i w różny sposób wybierając w każdym z łuków częściowych po jednym punkcie
. Jednakże gdy
rośnie nieograniczenie i gdy przy tym długość największego z łuków częściowych zmierza do zera, to wszystkie te sumy całkowe mają jedną i te samą wspólną granicę. Granicę tę nazywamy całką krzywoliniową (względem długości łuku) funkcji
po łuku
i oznaczamy symbolem
.

Podobnie określa się całki
,
,
względem rzutów łuku (czyli całki względem współrzędnych). Całki te określamy jako granicę sum całkowitych funkcji
wziętych po łuku
, z tą jedynie różnicą, że tworząc ich sumy całkowite wartości funkcji
w punktach
(łuku) mnożymy nie przez długości odpowiednich łuków częściowych
, lecz przez ich rzuty
lub
na osi układu.

Całka krzywoliniowa
oznacza sumę całek krzywoliniowych wyżej podanych postaci.

Całkę krzywoliniową po zamkniętej płaskiej linii
przy dokładnym kierunku obiegu tej linii (w kierunku przeciwnym do ruchu wskazówek zegara) oznaczamy symbolem
, a przy ujemnym kierunku obiegu symbolem
.

Zwykła (prostoliniowa) całka oznaczona jest szczególnym przypadkiem całki krzywoliniowej, w której linią całkowaną jest prostoliniowy odcinek osi układu.

Przy zmianie kierunku obiegu krzywej na przeciwny całka krzywoliniowa zmienia znak

Krzywą, po której przebiega całkowanie, wolno dzielić na części

Obliczenie całki krzywoliniowej
sprowadza się do obliczenia zwykłej całki oznaczonej. W tym celu korzystając z równania (lub z równań) linii całkowania
przekształcamy wyrażenie podcałkowe na funkcje jednej zmiennej. Wartości, jakie zamienna ta przebiera na początku i na końcu łuku
, określają granice otrzymanej całki oznaczonej.

Na ogół wartość całki krzywoliniowej zależy od tego, po jakiej linii całkujemy. Wartości całek branych wzdłuż różnych linii łączących punkty
i
mogą być różne.

Jeśli jednak w pewnym jednospójnym obszarze
wyrażenie
jest różniczką zupełną, to całka krzywoliniowa
nie zależy od drogi całkowania łączącej punkty
i
, a całka wzięta po dowolnej krzywej zamkniętej, lezącej w obszarze
, jest równa zeru.

Wyrażenie
jest różniczka zupełną funkcji
, w pewnym jednospójnym obszarze, jeżeli
i jeżeli
są ciągłe w tym obszarze.

Obliczanie wielkości za pomocą całek krzywoliniowych.

Całki krzywoliniowe, podobnie jak i pozostałe rodzaje całek oznaczonych służą do obliczania różnych wielkości geometrycznych i fizycznych.

Za pomocą całek krzywoliniowych łatwo oblicza się następujące wielkości;

1. Długość łuku
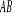
   płaskiej albo przestrzennej linii

2. Pole figury, lezącej na płaszczyźnie
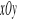
   i ograniczonej zamkniętą linią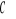
   

3. Masę
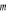
   łuku materialnego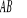
   

gdzie
oznacza gęstość liniową materiału w punkcie
łuku.

4. Współrzędne środka ciężkości
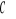
   łuku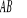
   

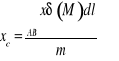
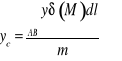
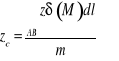
(W przypadku równomiernego rozkładu masy
wzory upraszczają się po wyłączeniu
przed znaki całek).

5. Pracę
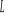
   , jaką wykazuje siła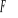
   działająca na punkt, przy jego przemieszczeniu się wzdłuż łuku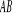
   

gdzie:
składowe siły wzdłuż osi współrzędnych.

Całki powierzchniowe i ich obliczanie przez zamianę na całki podwójne.

Niech funkcja
będzie określona i ciągła w każdym punkcie gładkiej powierzchni
. Podzielmy tę powierzchnię w dowolny sposób na
płatów częściowych polach równych
i wybierzmy w każdym z nich po jednym, dowolnym zresztą, punkcie
. Obliczamy wartości funkcji
w tych punktach i utwórzmy sumę

nazywamy sumę całkowita funkcji
wzglądem pola powierzchni
.

Ponieważ w opisanym tu procesie tworzenia sum całkowych powierzchnię
można dzielić na
płatów częściowych w różny sposób i w każdym z nich rozmaicie wybierać po jednym punkcie
, więc dla każdej danej funkcji
i dla każdej danej powierzchni
można utworzyć nieskończenie wiele różnych sum całkowych. Jeśli jednak dla
rosnącego nieograniczenie największa ze średnic płatów częściowych zmierza do zera, to wszystkie te sumy całkowe będą miały jedną i tylko jedną wspólną granicę. Granicę tę nazywamy całką funkcji
po płacie powierzchniowym lub całką względem pola powierzchni
i oznaczamy symbolem

Analogicznie określa się całki powierzchnie względem współrzędnych (względem rzutów płata)

Całki te są granicami sum całkowych funkcji
,
lub
branymi po powierzchni
, z tą jednak różnicą, że przy ich tworzeniu wartości funkcji w punktach
mnoży się ich przez pola
elementarnych płatów częściowych, lecz przez ich rzuty na płaszczyzny


układu współrzędnych.

Całka powierzchniowa względem współrzędnych o postaci ogólnej

jest sumą całe powierzchniowych współrzędnych.

Obliczanie całek powierzchniowych obu typów składa sprowadza się do obliczenia całek podwójnych po obszarze płaskim, W tym celu wychodząc z równania danej powierzchni
wyrażenie podcałkowe w całce powierzchniowej podstawiamy jako funkcję dwóch zmiennych, przebiegających obszar powstały przez zrzutowanie
na płaszczyznę układu odpowiadającą tym zmiennym.

Jeśli więc powierzchnia
, na którą rozciąga się całka powierzchniowa ma równanie
, to całkę powierzchniową pierwszego typu (po płacie powierzchni) zamieniamy na podwójną (a następnie obliczamy) wg wzorów

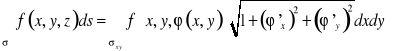
gdzie:
oznacza rzut obszaru
na płaszczyznę
.

Natomiast całkę powierzchniową drugiego typu (względem rzutów płata) zamieniamy na podwójną wg wzoru

Podwójny znak po prawej stronie równości wiąże się z tym, że całka występująca po lewej stronie może być rozciągnięta na dwie różne strony powierzchni
. Znak plus odpowiada całkowaniu po górnej stronie powierzchni
(zwróconej w stronę dodatniego kierunku osi
), minus - odpowiada całowaniu po dolnej stronie powierzchni
(zwróconej w stronę ujemnego kierunku osi
).

Jeśli na całej rozważanej powierzchni
zmiennej
nie można wyrazić jednoznacznie w funkcji
i
, to powierzchnię
trzeba podzielić na części, dla których jest to możliwe, a całkę braną po takiej powierzchni obliczyć jako sumę całek rozciągniętych na części składowe.

Analogicznie oblicza się całki powierzchniowe obu rodzajów, gdy powierzchnia
jest dana równaniem o postaci
albo
. Przy tym dla całek powierzchniowych drugiego typy przed całką podwójną stawia się znak plus albo minus, zależnie od tego, całka powierzchniowa jest brana po stronie powierzchni
zwróconej w dodatnim, czy też w ujemnym kierunku odpowiedniej osi układu (prostopadłej do płaszczyzny układu, na której leży obszar całkowania a całce podwójnej).

Całka powierzchniowa wzglądem współrzędnych
wzięta po płacie powierzchni cylindrycznej o tworzących równoległych do osi
jest równa zeru. W analogicznych przypadkach równe zeru są tez całki powierzchniowe względem współrzędnych
albo
.

Jeśli
jest powierzchnią zamkniętą, to całkę po zewnętrznej stronie powierzchni oznaczamy symbolem
a po wewnętrznej symbolem
.

Całkę po zamkniętej powierzchni
można przekształcić na całkę potrójną po obszarze
, ograniczonym tą powierzchnią, i na odwrót, za pomocą wzoru Gaussa-Ostrogradskiego

przy czym funkcje
wraz z pochodnymi pierwszego rzędu powinny być ciągłe w obszarze
.

Związek między całką po nie zamkniętej powierzchni
i całką krzywoliniową po konturze
, ograniczającym tę powierzchnię, dany jest wzorem Stokesa

przy czym funkcje
wraz z pochodnymi pierwszego rzędu powinny być ciągłe w obszarze
zawierającym
.

Kierunek obiegu konturu
i strona powierzchni
, po której całkujemy, związane są następującą regułą: obieg konturu
widzimy od tej strony powierzchni
, po której odbywa się całkowanie, powinien być przeciwny do ruchu wskazówek zegara.

Jeśli za pomocą powyższego wzoru przekształcimy całkę krzywoliniową po konturze zamkniętym na całkę powierzchniową, to jako
można przyjąć dowolną (kawałkami-gładką) powierzchnię, rozpięta na konturze
i pozostającą w obszarze
.

W przypadku gdy
jest płaskim obszarem
płaszczyzny

, powyższy wzór upraszcza się

Tę szczególną postać wzoru Stokesa nazywamy wzorem Greena.

Obliczanie wielkości za pomocą całek powierzchniowych.

1. Pole powierzchni
   

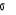
2. Masa powierzchni materialnej

gdzie:
oznacza gęstość powierzchniową rozkładu masy w punkcie
powierzchni

3. Współrzędna środka ciężkości
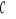
   powierzchni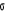
   

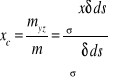
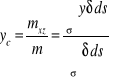
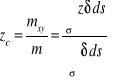
gdzie:
- momenty styczna powierzchni
względem układu.

Jeśli powierzchnia jest jednorodna, to
i wzory te upraszczają się po wyłączeniu
przez znaki całek.

Obszar płaski nazywamy jednospójnym, jeśli każda linię zamkniętą, lezącą w tym obszarze, można ściągnąć do punktu, nie wyprowadzając ja przy tym poza obszar.

Tak nazywamy powierzchnie, które w każdym swym punkcie maja określoną płaszczyznę styczną.

Dokładniej: przy odchodzeniu konturu
po stronie powierzchni
, po której całkujemy, przylegająca do konturu część powierzchni
powinna znajdować się z lewej strony.

---