TEMAT:
Metody całkowania cd. Miara i całka.

 

          (III)      OBLICZANIE CAŁEK Z UŁAMKÓW PROSTYCH II RODZAJU

 

                                                  całka I₁                       całka I₂         

 

 

 

                                                                                             całka I_n

 

 

 

Wyprowadzenie wzoru rekurencyjnego na I_n

                                                                              całka I



 

                                                             całka I_n

 

 

 

 

 

           (IV)      CAŁKOWANIE FUNKCJI NIEWYMIERNYCH

 

 

Metoda współczynników nieoznaczonych Lagrange'a

 

 

gdzie:      V_n-1(x)      - wielomian stopnia n-1 o nieznanych współczynnikach              

                
 - nieznana liczba

 

 Różniczkując obie strony równania otrzymujemy:

 

 

            Mnożąc obie strony równania przez
otrzymujemy:

 

 

 

 Przyrównując współczynniki przy odpowiednich potęgach wielomianów znajdujemy z
 otrzymanego układu równań nieznane współczynniki wielomianu V_n-1(x) oraz .

 

 <sup>Pozostaje znaleźć całkę
Powyższa całka daje się sprowadzić

             przez odpowiednie podstawienie do postaci:</sup>

 

 
   ^{gdy a>0}

 
                 ^{gdy a<0} 

 

 

 

PRZYKŁAD 3.1

 
            

           

 
           Różniczkując obie strony równania otrzymujemy:

 
          

 
           Mnożąc obie strony równania przez
otrzymujemy:

 
          

 
          
      

 
           Czyli:

                                                                                                                całka I₁

   

           Zatem:

          

 

 

 

PRZYKŁAD 3.2

                

               

 

 

Podstawienie Eulera

           
  
            gdzie R jest funkcją wymierną;

 

 

PRZYKŁAD 3.3

 

 

Całka sprowadzalna do typu Lagrange'a

 

 

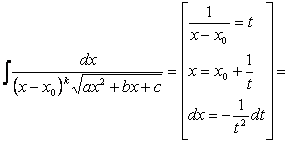
po przekształceniach

 

 

 

 

 

 

 

         (V)      CAŁKOWANIE FUNKCJI NIEWYMIERNYCH c.d.

                

 

            po wstawieniu otrzymujemy całkę z funkcji wymiernej

                gdzie: s - największa wspólna wielokrotność liczb q₁,q₂,...,q_k

 

 

 

PRZYKŁAD 3.4

 

 

 

 

 

 

 

          (VI)       CAŁKOWANIE FUNKCJI TRYGONOMETRYCZNYCH

 
             1^o     

 

a)       
 (przynajmniej jedna nieparzysta, np.
)

 

 

 

 

 

 

b)       
(obie parzyste)

zasada: zamieniamy na funkcję podwojonego kąta

 

                        zał:
      

 

wymnażamy

i dostajemy całkę tego samego typu

 

korzystamy ze wzorów:    
;
;

 

 

 

PRZYKŁAD 3.5

 

                       

 

                         Niech:    I₁=  

                                                I₂=

 

 

 

 

 

 

 

 

              2^o     
                       

 

korzystamy ze wzorów:

 

           

                                                                                    

 

              3^o

      

 

 

 

 

PRZYKŁAD 3.6

  
{z 1-ki trygonometrycznej}
   

 

              
             
         
             

              4^o
                     

 

 

  

 

            Metoda zasłaniania          gdy w mianowniku mamy tylko iloczyn
                                                                        wielomianów stopnia 1 w potędze 1

 

              
             

 

                    bo:     
              dla t=1              

 

                   

 

                    bo:    
            dla
          

 

        

 

 

 

MIARA I CAŁKA

 

 

DEFINICJA 3.1    (ILOCZYN KARTEZJAŃSKI)

 

A,B - zbiory

          
^{- iloczyn kartezjański zbiorów A i B}

            A₁,...,A_n - zbiory

          
  ^{- iloczyn kartezjański zbiorów A}₁^,...,A_n
 

 

 

DEFINICJA 3.2    (RODZINA PODZBIORÓW)

 

- zbiór,       
- zbiór wszystkich podzbiorów

 

               
            
 - rodzina podzbiorów zbioru

 

 

PRZYKŁAD 3.7

 
               

              

              

 

 

 

 DEFINICJA 3.3     (POŁĄCZENIE, PRZECIĘCIE)

 

               

              
   

              
^{- rodzina podzbiorów zbioru}

        

             
^{- połączenie zbiorów rodziny}

           
^{- przecięcie zbiorów rodziny}

 

              
<sup>dla i>0                

              
  dla i<0</sup>                
               

   
          

---