1. Podać i udowodnić twierdzenie o splocie w dziedzinie czasu dla transformaty Fouriera
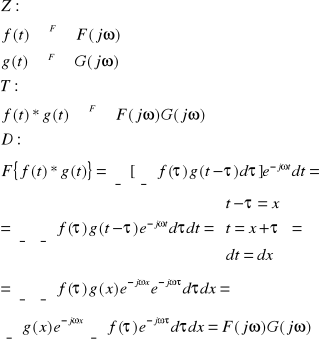
2. Podać ogólna postać wzorów Eulera-Fouriera opisujących funkcje f(t) w przedziale <0,T> w szereg ortogonalny o bazie φ
3. Jakie symetrie posiada widmo amplitudowe i widmo fazowe rzeczywistego sygnału okresowego? Skąd wynikają te symetrie ? (Jaka jest relacja pomiędzy Fk a F-k)
Widmo amplitudowe jest symetryczne względem osi ![]()
Widmo fazowe jest symetryczne względem początku układu współrzędnych.
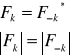
4. Podać dwa sposoby obliczania mocy sygnału okresowego, jeśli znamy jego przebieg w czasie, f(t), oraz współczynniki rozwinięcia w zespolony szereg Fouriera, Fk
f(t) 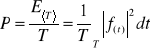
Fk ![]()
![]()
5. Podać twierdzenia dla przekształcenia Fouriera: o przesunięciu w dziedzinie czasu oraz o modulacji (czyli o przesunięciu w dziedzinie częstotliwości).
Założenie do obydwóch:
![]()
W dziedzinie czasu: ![]()
Dowód:
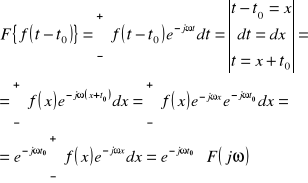
W dziedzinie częstotliwości: ![]()
Dowód:
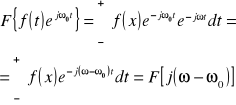
6. Podać dwa sposoby na obliczanie energii sygnału nieokresowego, jeśli znamy jego przebiegi w czasie f(t), oraz transformatę Fouriera F(jω).
1) 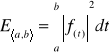
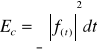
2) 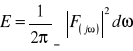
7. Jeżeli na wejście układu LTI o odpowiedzi impulsowej h(t) podamy sygnał u(t), to co zaobserwujemy na wyjściu układu ? (Jaka jest relacja pomiędzy y(t) a u(t) oraz h(t)?)
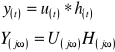
8. Podać (bez dowodu) twierdzenia dla przekształcenia Fouriera: o przesunięciu w dziedzinie czasu oraz o modulacji (czyli o przesunięciu w dziedzinie częstotliwości).
W dziedzinie czasu: ![]()
W dziedzinie częstotliwości: ![]()
Patrz na zadanie 5
9. Podać dwie postacie twierdzenia Parsevala: dla zespolonego szeregu Fouriera oraz dla transformacji Fouriera.
Dla transformacji Fouriera (widmo gęstości energii):
![]()
Dowód:
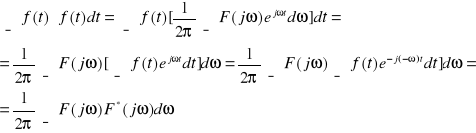
Dla zespolonego szeregu Fouriera:
![]()
![]()
Dowód:
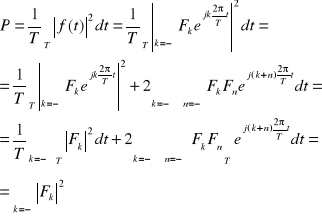
10. W jakich maksymalnych odstępach można pobrać próbki sygnału f(t) = A Sa2 (ω0t), aby możliwe było idealne odtworzenie tego sygnału z ciągu jego próbek? Obliczyć wartości próbek, f(nTs) podanych zgodnie z tą regułą, dla n = -2, -1, 0, 1, 2
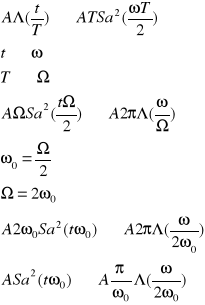
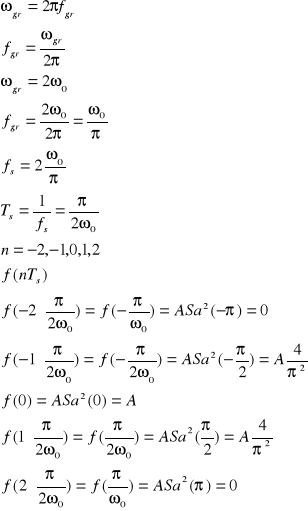
11. Podać pełną postać twierdzenia Parsevala dla transformacji Fouriera.
![]()
Dowód:
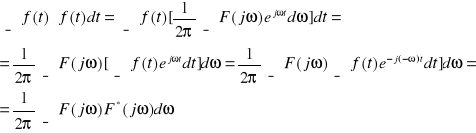
12. Podać twierdzenie o zmianie skali dla przekształceń Fouriera.
Założenie:
![]()
Twierdzenie:
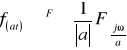
Dowód:
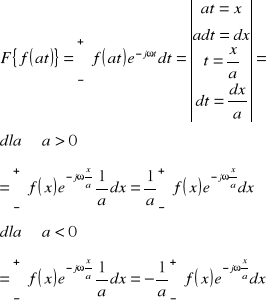
13. Podać (lub wyprowadzić) wzór opisujący transformatę Fouriera sygnału okresowego o znanych współczynnikach Fk rozwinięcia w zespolony wykładniczy szereg Fouriera.
![]()
14. Podać (lub wyprowadzić) wzór opisujący funkcję ruy korelacji wzajemnej wejścia i wyjścia układu LTI. (by Rybol)
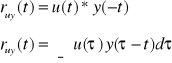
15. Podać (bez dowodu) twierdzenie o modulacji w dziedzinie czasu dla transformacji Fouriera.
![]()
16. Podać (bez dowodu) twierdzenie o całkowaniu dla transformacji Fouriera.
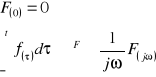
I i II pochodna
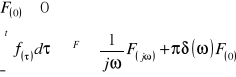
17. Podać wzór opisujący transformatę Fouriera sygnału spróbkowanego.(by Zbyyynek)
![]()
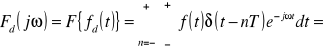
![]()
18. Twierdzenie o symetrii dla przekształcenia Fouriera mówi ze jeśli f(t) -> F(jω) to:
Założenie:
![]()
Twierdzenie:
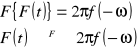
Dowód:
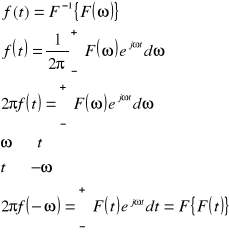
19. Transformata Fouriera sygnału okresowego o okresie T i współczynnikach Fk rozwinięcia w zespolony szereg Fouriera ma postać:
![]()
20. Odpowiedz idealnego układu całkującego na impuls Diracka wynosi:
Skok jednostkowy - 1(t)
21. Funkcja autokorelacji sygnału o skończonej energii f(t) jest opisana wzorem:
![]()
22. Sygnał spróbkowany ma widmo: (by Cis) okresowe
23. Opóźnienie grupowe w układzie LTI ma postać:
![]()
24. Składowa stała |sin(ω0t-π/4)|
Przesunięcie w sinusie nie ma znaczenia :D
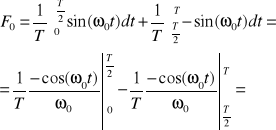
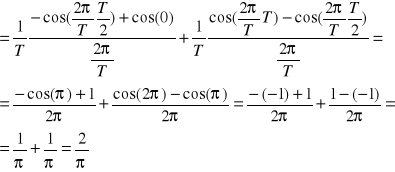
25. Ciąg współczynników rozwinięcia sygnału okresowego f(t) w zespolony szereg Fouriera posiada właściwość Fk = F*-k gdzie * oznacza sprzężenie gdy: (by Cudko)
gdy f(t) jest sygnałem rzeczywistym
26. Obliczyć wartość skuteczną U napięcia zmiennego opisanego wzorem
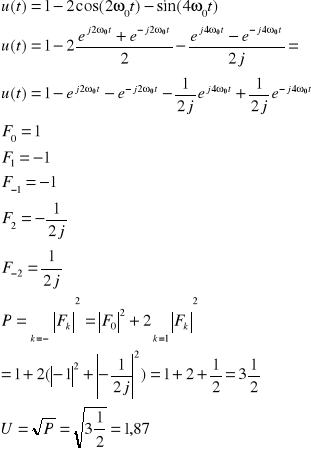
Wyszukiwarka
Podobne podstrony:
probkowanie sygnalu teoria
KWANTYFIKATORY some any no a lot of much many a little a few CWICZENIA I TEORIA NOWE
nowe pytania, 2 ROK, 3ci SEMESTR, Teoria Sygnałów
nowe pytania(27), 2 ROK, 3ci SEMESTR, Teoria Sygnałów
Pytania sesja1, ZiIP, 2 sem, Teoria sygnalow, Różne
Pytania sesja5, ZiIP, 2 sem, Teoria sygnalow, Różne
Nowe media a komunikowanie masowe, Materiały, Teoria komunikowania masowego
2Filtry analogowe, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, semestr V (moduł C), T
Ćw. 2. Sygnały elektryczne, Elektrotechnika - notatki, sprawozdania, Teoria obwodów, sprawozdania
kolots2002, ZiIP, 2 sem, Teoria sygnalow, Różne
Offe - nowe ruchy społeczne, Politologia, Politologia II, Teoria polityki, Teoria polityki, ćwiczeni
koszałka,teoria sygnałów, Podobieństwo sygnałów – korelacja
koszałka,teoria sygnałów, Widmo sygnału
sygnały spr okna, pwr, air, semestr 3, Teoria sygnałów
koszałka,teoria sygnałów, Filtry cyfrowe
więcej podobnych podstron