Temat: „ ZASADY OPRACOWANIA WYNIKÓW POMIARU WIELKOŚCI MIERZONYCH W GEODEZJI ORAZ ELEMENTY RACHUNKU WYRÓWNAWCZEGO”

1. Podstawowe wielkości mierzone w geodezji.

Przy pomiarach geodezyjnych określamy wielkości elementów liniowych (długości poziome, długości pionowe) i kątowych (kąty poziome i kąty pionowe)

Długość pozioma - odcinek między dwoma punktami zredukowany do poziomu.

Długość pionowa - różnica wysokości między punktami.

Kąt poziomy -kątem poziomym nazywamy kąt zawarty między rzutami osi celowych na płaszczyznę poziomą (płaszczyznę limbusa).

Kąt dwuścienny zawarty pomiędzy dwoma płaszczyznami kolimacyjnymi, przecinających się wzdłuż pionowej krawędzi VV, realizowanej przez oś obrotu instrumentu, która łączy środek limbusa ze środkiem znaku geodezyjnego. Miara kata dwuściennego jest kąt płaski leżący na płaszczyźnie prostopadłej do pionowej krawędzi VV.

Kąt pionowy - jest to kąt obydwa ramienia którego leżą na jednej płaszczyźnie pionowej, przy czym jedno ramie kata jest zawsze stałe (pionowe lub poziome) a drugie zmienne.

2. Jednostki miar.

2.1 Podstawowe jednostki układu SI:

• długość - metr (m)

• masa - kilogram (kg)

• czas - sekunda (s)

• natężenie prądu - amper (A)

• temperatura - kelwin (K)

• ilość materii - mol (mol)

• światłość - kandela (cd)

2.2 Miary długości

Metr - odcinek w którym mieści się 1 650 763,73 długości fal świetlnych wysyłanych w próżni przez rozżarzony gaz krypton. Stanowi w przybliżeniu 10^-7 ćwiartki południka ziemskiego.

Metr jest to długość drogi przebytej w próżni przez światło w czasie 1/299 792 458 sekundy.

1m = 10dcm = 100 cm = 1000 mm

100 m - hektometr

1000 m - kilometr

2.3 Miary powierzchni.

1m² = 0,01dcm² = 0,0001 cm² = 0,000001 mm²

1ar = 100m²

1ha = 100 ar = 10 000m²

2.4 Miary kątowe.

Stopień - jest to 1/360 kąta pełnego - układ sześćdziesiętny

1^o = 60' = 3600''

Grad - jest to 1/400 kąta pełnego- układ dziesiętny

1centygrad = 1/100 grada

1 decymiligrad = 1/10 000grada = 1/100 centygrada

1^g = 100^c =10 000^cc

Zależność między stopniem i gradem:

1g =
1⁰ =

1^c =
1'=

1^cc =
1'' =

Przykład:

25^o 15' 30'' = 25^o 15',5 = 25^o,2583₍₃₎

25^o,2583₍₃₎ x
= 28,0648^g

28^g06^c48^cc

Radian - jest to kąt środkowy oparty na łuku równym promieniowi.

Wartość ρ dla podziału stopniowego:

ρ^o =
= 57,29578⁰

ρ^o =
= 3437,75'

ρ^o =
=206265''

Wartość ρ dla podziału gradowego:

ρ^g =
= 63,6620^g

ρ^c =
= 6366,20^c

ρ^cc =
=636620^cc

3. Pojęcia liczb dokładnych i przybliżonych.

Liczba znana z dokładnością nieograniczoną i dająca się zapisać bez błędu nazywa się liczbą dokładną.

V= 4/3 ၰR³ ; M = 100ზ5

Wynikiem każdego pomiaru są wyniki liczbowe, które wobec nieznanej wartości prawdziwej są liczbami przybliżonymi i ich dokładność jest ograniczona.

Cyfry dziesiętne - wszystkie cyfry położone na prawo od przecinka dziesiętnego.

Cyframi znaczącymi (pewnymi) nazywamy wszystkie cyfry liczby przybliżone, z wyjątkiem zer położonych na lewo od pierwszej różnej od zera cyfry, a także z wyjątkiem wszystkich cyfr niepewnych (obniżonych lub dopisanych drobnym drukiem). Cyfry znaczące określają stopień przybliżenia.

Przykład:

1. 0,00345 - 3 cyfry znaczące;

2. 3450 - 4 cyfry znaczące;

3. 0,314₅ - 3 cyfry znaczące;

4. 34,5004 - 6 cyfr znaczących

Błąd „krańcowy”(granica błędu) - jest to połowa ostatniej nie napisanej cyfry znaczącej

Przeważnie mamy do czynienia z liczbami przybliżonymi o znanym stopniu przybliżenia :

(X₀ - ၄x)<X<(X₀ + ၄x)

X₀ - znane przybliżenie

၄x - błąd krańcowy (granica błędu)

X - liczba przybliżona

Zapis błędu krańcowego: ± 5*10^-k

Przykład:

1. 0,70711 - 0,000005 < sin 45^o < 0,70711 + 0,000005

0,707105< sin 45^o < 0,707115

2. Jaki jest błąd krańcowy zapisu liczby ၰ (3,14):

3,135 < ၰ < 3,145

Odpowiedz: ± 5 *10 ^-3

W zapisie dziesiętnym liczby, zera końcowe mogą mieć dwojakie znaczenie:

• wskazują rząd wielkości liczby

• charakteryzują dokładność liczby

Przykład:

100km = 100 000m

၄x = 0,5 km ၄x = 0,5 m

Prawidłowy zapis: 100 km = 100 * 10³ m

4. Reguły zaokrąglenia.

1. Jeżeli pierwszą z odrzuconych cyfr jest mniejsza od 5, to liczbę zaokrąglamy „w dół”, pozostawiając ostatnią cyfrę znacząca bez zmian;

2. Jeżeli pierwsza z odrzuconych cyfr jest większa od 5 - liczbę zaokrąglamy „w górę”, powiększając ostatnią cyfrę znaczącą o jeden;

3. Jeżeli pierwszą z odrzuconych cyfr jest 5 lecz następuje po niej co najmniej jedna cyfra inna niż zero, to ostatnią pozostawioną cyfrę zwiększamy o 1.

4. Jeżeli odrzuconą cyfra jest 5 a po niej nie występuję inna cyfra niż zero, to ostatnią pozostawiona cyfrę zwiększamy do najbliższej parzystej.

Przykład:

1. 1233,6545m Ⴛ 1233,65 m ( odległość)

2. 1233,6545 m² Ⴛ 1234 m² ( powierzchnia)

3. 1233,65450 m Ⴛ 1233,654 m (rzędna wysokości)

4. 1233,654501m Ⴛ 1233,655 m

5. 1233,6545 m ≈ 1233,654 m

6. 1233,6535 m Ⴛ 1233,654m

5. Reguły Bradis - Kryłowa

1. W sumowaniu algebraicznym liczb przybliżonych należy w wyniku pozostawić tyle miejsc dziesiętnych ile ich zawiera liczba z najmniejszą ilością miejsc dziesiętnych:

9,01 + 21,5 + 12,456 = 42,9661 zapis prawidłowy 43,0

11 + 0,11 - 0,0011= 11,1089 zapis prawidłowy 11

2. Ilość cyfr znaczących w ilorazie (w iloczynie) równa się ilości cyfr znaczących w tym jego czynniku, który zawiera najmniej cyfr znaczących:

2,5*2,000= 5,0

1: 0,001= 1000 prawidłowy zapis 1*10³

3. W potęgowaniu (pierwiastkowaniu) liczb przybliżonych należy pozostawić tyle cyfr znaczących ile ich zawiera liczba o najmniejszej ilości cyfr znaczących:

(2,0x0,02)² = 0,16 prawidłowy zapis = 0,2

ზ 5x20 = 10 - // - =1x10

4. W obliczeniu wyników pośrednich należy zawsze brać jedną cyfrę dodatkową (cyfrę niepewną) niż wykazują reguły 1-3 .

„Zapasową” cyfrę zapisujemy drobniejszym pismem:

14,28₃ + 25,5₁ = 39,7₉₃ = 39,8

5. Jeżeli niektóre liczby przybliżone zawierają więcej znaków dziesiętnych (przy dodawaniu lub odejmowaniu) lub więcej cyfr znaczących (mnożenie dzielenie potęgowanie pierwiastkowanie) niż pozostałe to należy je przede wszystkim zaokrąglić, pozostawiając jedną zbędną cyfrę:

20,52 + 1,0 + 1,015899000004= 20,53 +1,0 + 1,0₂ = 22,5₅ = 22,6

7. Jeżeli dane wyjściowe można brać z dowolną dokładnością, wówczas aby otrzymać wynik o k cyfrach, należy brać dane z taką ilością cyfr, które zgodnie z regułami 1-3 dają w wyniku k+1 cyfr:

Przykład zastosowania reguł:

Działanie:

345,8275 + 25,461 + 618,3

rachunek według reguł:

345,83 + 25,46 +618,3 = 989,59 Ⴛ 989,6

6. Elementy rachunku wyrównawczego i metody obliczeń geodezyjnych

6.1 Błędy obserwacji geodezyjnych.

6.1.1 Źródła błędów:

• niedoskonałość zmysłów obserwatora

• błędy przyrządów i instrumentów

• warunki pomiaru.

6.1.2 Błędy pomiarowe:

trzy grupy błędów:

• błędy grube (omyłki) - mają dużą wartość liczbową, spowodowane nieuwagą lub omyłką obserwatora,

• błędy systematyczne - powstają wskutek działania ustalonych prawidłowości w określonych warunkach pomiaru (instrumentalne, osobowe, środowiskowe),

• błędy przypadkowe - mają charakter losowy i są nie możliwe do wyznaczenia lub wyeliminowania ze względu na ich losową zmienność wartości liczbowych oraz znaku. Można zmniejszyć wpływ błędów przypadkowych poprzez wyrównanie - doprowadzając obserwację do wzajemnej matematycznej zgodności z jednoczesnym dokonaniem oceny dokładności po wyrównaniu.

6.1.3 Prawo błędów Gaussa .

Wartość prawdziwa mierzonej wielkości:

^{X = L}_i ^+ξ_i

gdzie: X - wartość prawdziwa

Li - obserwacja (spostrzeżenie)

ξ_i - błąd prawdziwy

Prawdopodobieństwo występowania błędów przypadkowych - prawo błędów Gaussa - Laplace΄a:

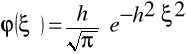
gdzie:

ϕ(ξ) - funkcja określająca szybkość zmiany prawdopodobieństwa pojawienia się błędu przypadkowego ξ

ξ - przypadkowy błąd prawdziwy

h - parametr związany z warunkami wpływającymi na

dokładność pomiaru

e - podstawa logarytmu naturalnego e= 2,718 281 828...

π = 3,141 592 653....

Wnioski na podstawie analizy krzywej Gaussa:

• Najbardziej prawdopodobne jest pojawienie się błędów przypadkowych równych zero.

• Prawdopodobieństwo błędu mniejszego jest większe niż prawdopodobieństwo błędu większego.

• Prawdopodobieństwo błędów o tej samej wartości bezwzględnej lecz o przeciwnych znakach jest jednakowe.

• Zwiększenie dokładności pomiaru powoduje zmniejszenie prawdopodobieństwa pojawienia się błędów o dużych wartościach liczbowych.

• Przy zwiększeniu ilości obserwacji suma błędów przypadkowych dąży do zera.

6.1. Zadanie i cel rachunku wyrównawczego.

Zadania:

• wyznaczenie najbardziej prawdopodobnych wielkości wartości mierzonych

• określenie dokładności wielkości mierzonych oraz funkcji tych wielkości.

Cele:

- znalezienie poprawek i wyrównanie pomiarów pod warunkiem wykonania obserwacji nadliczbowych i wyeliminowania błędów grubych i systematycznych.

• badanie zgodności spostrzeżeń i charakteru popełnionych błędów

• znajdowanie niewiadomych danego zagadnienia

• prognozowanie a'priori.

Wyrównaniem obserwacji nazywamy poprawienie wielkości obserwacyjnych przez dodanie do nich odpowiednich poprawek (błędy pozorne) w celu uzyskania wartości najbardziej prawdopodobnych. _

l_i+v_i = L

gdzie : _

L - wartość najbardziej prawdopodobna

l_i - obserwacja

v_i - błąd pozorny

6.1.7 Ocena dokładności obserwacji:

Do oceny dokładności w geodezji korzystamy z pojęcia błąd średni

m - błąd średni

3m - błąd graniczny - jego przekroczenie jest mało

prawdopodobne (1: 370)

Prawdopodobieństwo nie przekroczenia średniego błędu wynosi 0,68.

Często do oceny dokładności pomiaru określonym przyrządem lub określoną metodą stosuje się błąd względny, przeciętny, błąd prawdopodobny:

• Błąd absolutny - błąd przypadający na całość mierzonej wielkości (m - średni błąd bezwzględny).

• Błąd względny - błąd przypadający na jednostkę mierzonej wielkości (m/d - gdzie d jest cała mierzona wielkość).

• Błąd przeciętny t - jest to średnia arytmetyczna z bezwzględnych wartości błędów pozornych (poprawek) lub błędów prawdziwych:

t´ = [|v|] / n t= [|ξ|] / n

• Błąd prawdopodobny r - jest to błąd którego prawdopodobieństwo przekroczenia równe jest prawdopodobieństwu nieprzekroczenia i wynosi 0,5.

r = 0,67449 m gdzie m - średni błąd

1. Wyrównanie obserwacji bezpośrednich.

Rachunek wyrównawczy opiera się na teorii najmniejszego kwadratu, rachunku prawdopodobieństwa i doświadczeniu.

Wszystkie obserwacje dzielą się na bezpośrednie i pośredniczące.

Obserwacje otrzymane w wyniku porównania wielkości mierzonej z podziałką przyrządu mierniczego podczas wielokrotnych pomiarów tej samej wielkości mierzonej nazywamy spostrzeżeniem bezpośrednim.

Spostrzeżenia, które nie odnoszą się bezpośrednio do wielkości szukanych, lecz służą do wyznaczenia niewiadomych za pomocą ustalonych związków funkcyjnych, nazywamy pośredniczącymi.

6.2.1 Wyrównanie obserwacji bezpośrednich jednakowodokładnych.

Spostrzeżenia (obserwacje) jednorodne wykonane o identycznych źródłach błędów nazywamy spostrzeżeniami jednakowodokładnymi.

Spostrzeżenia tworzą określony zbiór i mają charakter spostrzeżeń typowych (charakteryzują się jednakowym błędem średnim):

m₁ = m₂ = ... = m_i

Wielkość najbardziej prawdopodobna - średnia arytmetyczna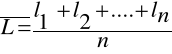
z obserwacji, spełniająca związek:

L= l_i + v_i

W wyniku wyrównania uzyskujemy poprawki v:

_

v_i = L- l_i

Dobór poprawek powinien nastąpić w oparciu o teorię najmniejszych kwadratów:

v²₁ + v²₂ + v²₃ + ... + v²_n = [vv] = minimum

Suma poprawek spełnia zależność:

_

[v] = n x L - [l] albo [v] = 0

Ocena dokładności:

_

l_i = L-ξ_i = L - v_i

średni błąd pojedynczego spostrzeżenia:

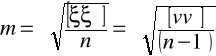
średni błąd średniej arytmetycznej:

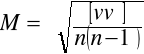
6.2.2 Wyrównanie spostrzeżeń bezpośrednich

niejednakowodokładnych.

Waga jest to liczba dodatnia wyrażająca stopień zaufania do spostrzeżenia - p.

p = 1 - jest to waga typowego spostrzeżenia

Zależność wag:

p₁:p₂ : ... : p_i = k/m²₁ : l/m²₂ ... : n/m²_i

gdzie k, l, n - ilość pomiarów w każdej grupie

Wartość wyrównana - ogólna średnia arytmetyczna (średnia ważona):

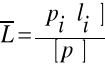
Ocena dokładności:

_

ν= L -l_i

-
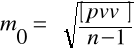
średni błąd typowego spostrzeżenia

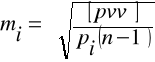
- średni błąd i-tego spostrzeżenia

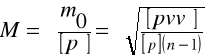
- średni błąd średniej ważonej.

6.3 Prawo przenoszenia się błędów

Błędy wielkości obserwacyjnych powodują, że funkcje tych wielkości też są obarczone błędami (wyrównanie pośredniczących spostrzezen).

Dla funkcji nieliniowych:

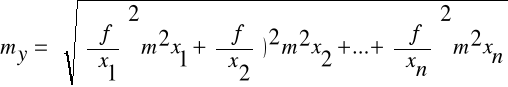
Dla funkcji liniowych:

1. Zdefiniować jednostki w których mierzymy kąty płaskie i podać relacje pomiędzy nimi./np. w mierze analitycznej (radianach) wartość kąta 18^g/

2. Zdefiniować wielkości które mierzymy w geodezji, podać przykłady przyrządów, którymi mierzymy te wielkości.

3. Jak powinny być zapisywane wyniki pomiarów i obliczeń?

4. Jaką liczbę nazywamy przybliżoną i co nazywamy błędem krańcowym liczby przybliżonej? / zilustrować przykładem/

5. Wymień rodzaje błędów popełnianych w pomiarach inżynierskich i ich źródła.

6. Zdefiniować pomiary bezpośrednie i pośrednie. /podać przykłady/

7. Podać i objaśnić wzory na najbardziej prawdopodobny wynik wielkości mierzonych w pomiarach jednakowodokładnych i niejednakowodokładnych.

8. Jakim błędem będzie obarczony wynik objętości np. graniastosłupa wg prawa przenoszenia się błędów?

9. Objaśnić pojęcie błędów: prawdziwego, pozornego, granicznego, względnego.

---