Statystyka - pojęcia i wzory.
Statystyka to nauka zajmująca się ilościowymi metodami analizy zjawisk masowych. Przy czym masowość zjawiska polega na jego wykorzystaniu dla dużej liczby jednostek statystycznych (obiektów) właśnie dzięki temu możliwe jest wykrycie za pomocą metod statystycznych różnego rodzaju prawidłowości występujących w gospodarce np. skłonności ludzi do oszczędzania, polityka kredytowa banków, zachowanie przedsiębiorstw.
Przedmiotem badań w statystyce jest zbiór jednostek statystycznych podobnych pod względem określonych własności (np. mieszkańcy Katowic, oddziały banków) nazywamy populacją ( zbiorowością statystyczną ). Ponieważ bezpośrednie badania populacji są zbyt kosztowne i czasochłonne, a często wręcz niemożliwe zatem w statystyce do analizy wykorzystuje się najczęściej próbę, która stanowi podzbiór populacji.
Rodzaje cech (reprezentowanych przez zmienne)
*jakościowe (mierzalne)
np. płaca, koszty produkcji
*skokowe (przyjmują wartości ze skończonego zbioru wartości )
np. liczba studentów w grupie itp.
*ciągłe (przyjmują wartości z nieprzeliczalnego zbioru wartości) wynika to z dokładności pomiaru, np. wzrost, waga, wartość sprzedaży itp.
Szeregi
*szczegółowy
np. płaca w tys. złotych (0,89 0,23 1,2 3,8 0,45 2,5)
*rozdzielczy dla ceny skokowej
liczba oddziałów |
liczba banków |
1 |
7 |
2 |
12 |
3 |
9 |
4 |
2 |
razem |
30 |
*dla ceny ciągłej
wielkość lokaty |
liczba kont |
do 1000 |
154 |
1000-2000 |
585 |
2000-3000 |
378 |
3000-4000 |
297 |
4000 i więcej |
125 |
razem |
1539 |
wykres histogram:
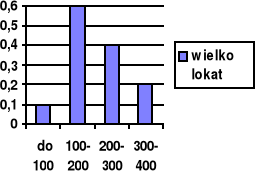
Miary służące do opisu cech jednostek statystycznych należących do próby:
*miary przeciętne (średnie) charakteryzują średnią wartość cechy dla jednostek w próbie.
*miary zróżnicowania (zmienności) charakteryzują stopień zróżnicowania jednostek w próbie
*miary asymetrii pokazują czy więcej jednostek ma wartość cechy większej lub mniejszej od średniej.
Średnia
*arytmetyczna dla szeregu szczegółowego
![]()
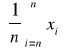
*arytmetyczna dla szeregu rozdzielczego cechy skokowej
![]()
*arytmetyczna szeregu rozdzielczego cechy ciągłej
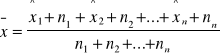
![]()
-to środek przedziału klasowego
*arytmetyczna w przypadku częstości względnych
![]()
*harmoniczna
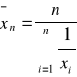
*geometryczna
![]()
Dominanta (moda)
to wartość cech, które występują najczęściej (jest typowa)
*szereg szczegółowy- wartość występująca najczęściej
*szereg rozdzielczy dla cechy skokowej- wartość o największej liczebności
*szereg rozdzielczy dla cechy ciągłej- wartość leżąca w przedziale o największej liczebności
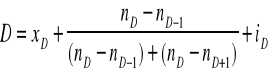
xD -dolna granica przedziału dominanty
nD liczebność przedziału dominanty
nD-1 liczebność przedziału poprzedniego
nD+1 liczebność przedziału następnego
iD szerokość przedziału dominanty
Kwartyle
dzielą uporządkowany rosnąco (lub malejąco) według wartości określonej cechy zbiór jednostek na odpowiednią liczbę części.
Kwartyle- podział na 4 części
25% 25% 25% 25%
xmin Q1 Me Q2 xmax
Q1 kwarty pierwszy dzieli jednostki na dwie części 25% z nich ma wartość cechy mniejszej od niego zaś 75% większe.
Me mediana dzieli jednostki na dwie równe części, połowa ma wartość cechy mniejszej a połowa większej
Q2 kwartyl trzeci dzieli jednostki na 2 części 75% z nich ma wartość cechy mniejszej od niego zaś 25% większej.
Mediana
Szereg szczegółowy należy uporządkować rosnąco i obliczyć:
![]()
gdy n jest nieparzyste
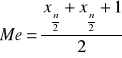
gdy n jest parzyste
Szereg rozdzielczy dla cechy skokowej należy skumulować liczebność lub części względne i znaleźć wartość dla której częstość >=50%
szereg rozdzielczy dla cechy ciągłej skumulować liczebność i znaleźć przedział w którym częstość względna >=50% oraz wykorzystać wzór:
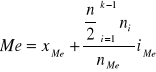
x -dolna granica przedziału mediany
n -liczebność przedziału mediany
i -szerokość przedziału mediany
n -liczebność próby
Kwartyle
1.
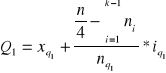
3.
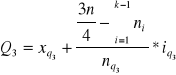
Odchylenie ćwiartkowe (pozycyjna miara rozproszenia)
Przeciętne zróżnicowane wartości zmiennej.
![]()
Gęstość -gdy przedziały są różnej szerokości
![]()
zależność między wszystkimi przeciętnymi
![]()
Pozycyjna miara asymetrii.
![]()
[-1,1]
Pozycyjny współczynnik zmienności
![]()
Współczynnik skośności Pearsona
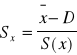
Współczynnik zmienności (porównywanie różnych rozkładów)
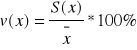
Odchylenie przeciętne
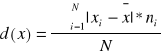
Wyszukiwarka
Podobne podstrony:
Egzamin II ze statystyki luty 2007
Wzory 24, Statystyka, Kasperowicz-Ruka
Rodowód, przedmiot?dań i podstawowe pojęcia statystyczne Uwagi na temat organizacji?dań stat
Podstawowe pojęcia statystyki
Egzamin z Metodologii ze statystyk kurs podstawowy
Wzory 21, Statystyka, Kasperowicz-Ruka
Statystyka - egzamin - ściąga - Kuszewski, Statystyka - wykłady - T.Kuszewski
Wzory na statystyke
Chemia wzory i pojęcia
Wzory 23, Statystyka, Kasperowicz-Ruka
Sciągi do egzaminu, sciaga pojecia
Wzory stat, Statystyka - podstawowe wzory
w1, Geneza pojęcia Statystyka
egzamin wzory lek
egzamin wzory lek (2)
Statystyka-egzamin-pytania, Podstawy statystyki
Podstawowe pojęcia statystyki
podstawowe pojęcia statystyka, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
więcej podobnych podstron