Nr ćwiczenia 26 |
Temat ćwiczenia Rezonans akustyczny |
Ocena z teorii |
Nr zespołu 10 |
Imię i Nazwisko Miłosz Gąsiorowski |
Ocena z wykonania |
Data 27.02.2001 |
Wydział, kierunek, rok, grupa EAIiE, Automatyka i Robotyka, rok 1, gr.2 |
Uwagi |
Konspekt.
Celem ćwiczenia jest obserwacja rezonansu fal akustycznych w rurze Quinckiego, pomiar prędkości dźwięku w powietrzu i CO2 oraz wyznaczanie stosunku cp/cv dla tych gazów
Zapoznanie się z podstawą teoretyczna ćwiczenia
Prędkość dźwięku wyznacza się w oparciu o zjawisko interferencji fal głosowych w rurze Quinckiego. Rozchodzenie się dźwięku można traktować jako lokalne zgęszczenia i rozrzedzenia gazu zachodzące adiabatycznie, dlatego można wykorzystać pomiar prędkości dźwięku do wyznaczania wielkości cp/cv charakteryzującą przemianę adiabatyczną gazu.
Głośnik wytwarza fale dźwiękową rozchodzącą się w rurze, którą można opisać równaniem y1=ym sin(kx-t)
Gdzie x odległość mierzona od położenia głośnika, w częstość kołowa k wektor falowy
W punkcie x=L fala odbija się na granicy ośrodków i porusza się z powrotem. Zaburzenie ośrodka w punkcie x pochodzące od fali odbitej wynosi y2=ymsin[k(L+L-x)-t+] ,L długość słupa powietrza, faza uwzględnia możliwa zmianę przesunięcia fazowego po obiciu.
W wyniku interferencji obu fal powstaje fala
Y= y1+ y2=2ymsin(-t+kL+/2)cos(kx-kL-/2)
![]()
Powierzchnia wody nie jest pobudzana stąd występuje tu x=L, węzeł y=0 . Jest to spełnione gdy cos(kx-kL-/2)=0 czyli Gdy występuje rezonans oznacza że na początku rury występuje strzałka a więc cos(kx-kL-/2)=1 stąd (-kL-/2)=n czyli
Zatem wzmocnienie dźwięku dostaniemy tylko dla ściśle określonych słupów gazów.
Należy zauważyć że sąsiednie długości rezonansowe różani się o /2.
Prędkość dźwięku w gazach.
Wyznaczanie długości fali umożliwia przy znanej częstotliwości obliczenie prędkości: v=f ·
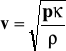
Przy rozchodzeniu dźwięku zmiany ciśnienia (zgęszczenia i rozrzedzenia) zachodzą tak szybko że nie występuje wymiana ciepła, czyli przemiany gazowe zachodzą adiabatycznie, w takim wypadku prędkość wynosi:
![]()
Z równania stanu gazu:
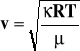
Otrzymujemy:
Z powyższego równanie widać że prędkość dźwięku nie zależy od ciśnienia, a ponieważ dla danej masy gazu jego skład(a zatem ciężar cząsteczkowy ) i temperatura są znane, równanie umożliwia obliczenie . Z kolei ta wartość zależy od ilości stopni swobody i molekuły gazu:
![]()
Wykonanie
Wypełniamy rurę wodą ustawiamy żądaną częstotliwość na generatorze i spuszczamy powoli wodę z rury wysłuchując pierwszego rezonansu notujemy położenie słupa wody i wysłuchujemy kolejnego rezonansu i notujemy położenie słupa, następnie obliczmy różnice położeń znajdując zarazem połówkę długości fali. Poważając pomiar 4-5 razy dla każdej z 4-5 częstotliwości z zakresu 400-1600 Hz.
Dla dwu tlenku węgla postępujemy odwrotnie napełniamy rurę do pełna zatykamy korkiem wcześniej usuwając głośnik otwieramy kurki dopływu gazu i spuszczamy powoli wodę zasysając gaz ze zbiornika. Gdy napełnimy rurę gazem ustawiamy głośnik i powoli napuszczamy wodę do rury i obserwujemy rezonans notując kolejne położenia.
Ponieważ mamy związek v=f najlepiej będzie rozważać wyniki przy pomocy regresji liniowej związku =v·1/f .
![]()
Ogólna zależność wyników w zależności liniowej:
Wzory na wyliczenie współczynników zależności liniowej, mając n par punktów pomiarowych xi yi zależnych liniowo.
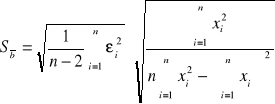
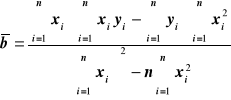
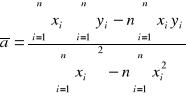
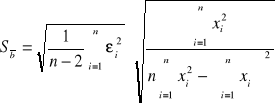
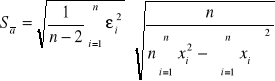
Sposób wyliczenia odchylenia standardowego:
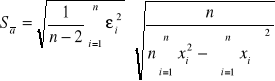
![]()
Widać ze wzorów że znaleziony współczynnik a jest wyznaczaną prędkością dźwięku w gazie
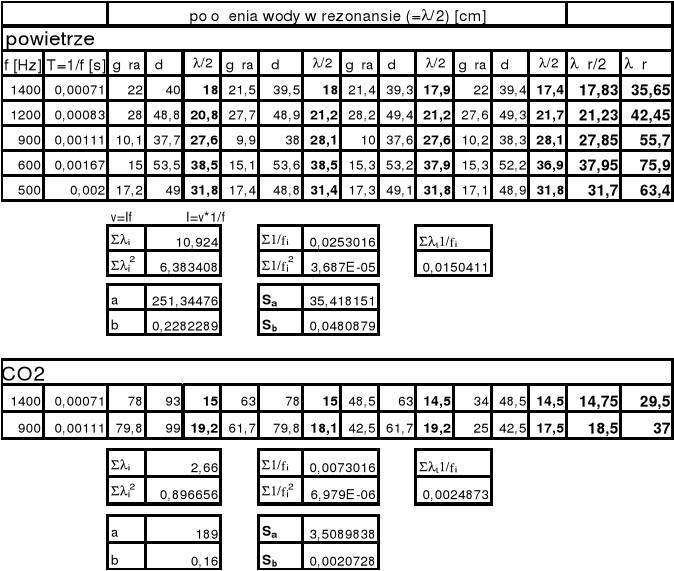
Niestety obliczenia nie dały rzeczywistego wyniku, pomiar posiada błąd systematyczny. Błąd ten mógł wystąpić z racji pomiaru słupa wody lub odczytu zadanej częstości na generatorze. Najbardziej prawdopodobna jest druga możliwość. Położenia słupa wody przy którym występował rezonans były łatwo wyróżnialne tylko w ściśle określonych miejscach następowało drażniące ludzkie ucho wzmocnienie natężenia tj. na długości ok. 5 cm.
Różnica między
Wyznaczenie k
Pomiary zostały przeprowadzone w temperaturze t=18,5oC czyli T=291.5 K
![]()
Stąd k=
![]()
![]()
K różni się od rzeczywistego o +2mn+n2 ,.gdzie m=v, n=vrzeczywiste-v (wynika to (m+n)2)
![]()
![]()
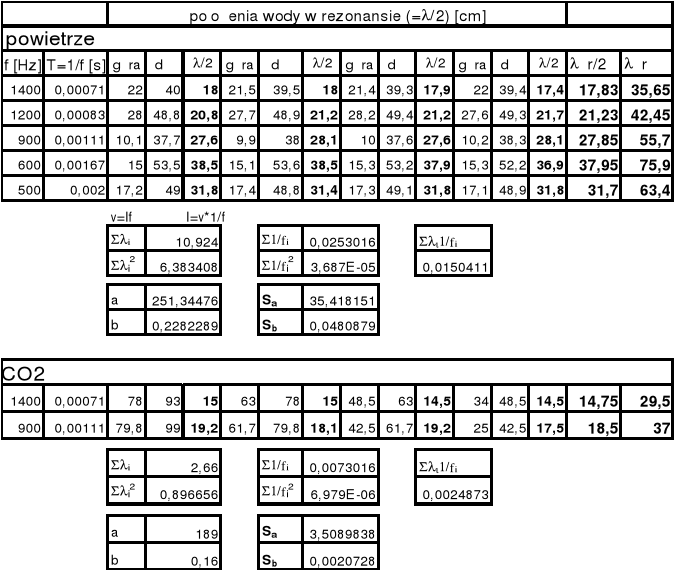
![]()
![]()
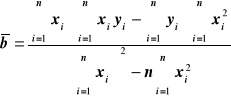
![]()
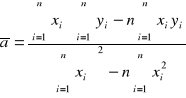
![]()
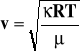
![]()
![]()
![]()
![]()
![]()
![]()
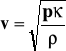
Wyszukiwarka
Podobne podstrony:
Lepkość-sciaga, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Nr ćwiczenia5 moje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[4]tabelka, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[8]konspekt new, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
FIZYK~47, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizyka
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
kospekt12, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 12 Wyznaczanie
PUZON, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki s
cw8 wyniki, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
mostek Wheatstone'a(1), Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, l
za, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, laborki fizy
konspekt nr8, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fi
[7]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
konspekt 8, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizy
konspekt 9, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizy
więcej podobnych podstron