POLITECHNIKA WROCŁAWSKA INSTYTUT METROLOGII ELEKTRYCZNEJ
Krzysztof Najdzionek	Sprawozdanie z ćwiczenia nr 5. Temat: Pomiary częstotliwości i przesunięcia fazowego.
Wydział Elektroniki Rok I	Data: 27.05.1998	Ocena:

1. Wykaz przyrządów użytych w ćwiczeniu.

• częstościomierz PFL-23,

• generator dekadowy RC typ PW-13,

• częstościomierz-czasomierz liczący typ C549A,

• częstościomierz analogowy LC-1,

• oscyloskop GoldStar OS-9020G,

• przesuwnik fazowy typy T.

2. Pomiar częstotliwości przyrządami cyfrowymi.

Wyniki pomiarów.

L.p.	PFL - 23			C - 549
		f	f	δf	T	T	fX	fX	δfX
		Hz	Hz	%	s	s	Hz	Hz	%
1	20	1	5,0	50,382*10^-3	0,001*10^-3	19,8484	0,0004	0,002
2	100	1	1,0	10,003*10^-3	0,001*10^-3	99,970	0,010	0,010
3	200	1	0,50	5,007*10^-3	0,001*10^-3	199,720	0,040	0,020
4	1000	1	0,10	1,001*10^-3	0,001*10^-3	999,001	0,998	0,100
5	2000	1	0,050	500,82*10^-6	0,01*10^-6	1996,73	0,04	0,002
6	5000	1	0,020	200,75*10^-6	0,01*10^-6	4981,32	0,25	0,005
7	8000	1	0,013	124,77*10^-6	0,01*10^-6	8014,75	0,64	0,008
8	10000	1	0,010	99,922*10^-6	0,001*10^-6	10007,81	0,10	0,001
9	14000	1	0,007	71,925*10^-6	0,001*10^-6	13903,37	0,19	0,001
10	18000	1	0,006	55,545*10^-6	0,001*10^-6	18003,42	0,32	0,002
11	20000	1	0,005	49,954*10^-6	0,001*10^-6	20018,42	0,40	0,002
12	50000	1	0,002	20,001*10^-6	0,001*10^-6	49997,50	2,50	0,005
13	100008	1	0,001	9,999*10^-6	0,001*10^-6	100010	10	0,010

Przykłady obliczeń.

f = +/- 1 na ostatnim miejscu

T = +/- 1 na ostatnim miejscu

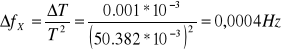
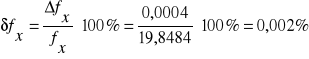
3. Pomiar częstotliwości napięcia sieci.

1. Częstościomierz cyfrowy PFL-23 przy amplitudzie sygnału 10V.

f = +/- 1 na ostatnim miejscu = 0,1 Hz

f = (50,4
0,1) Hz

2. Częstościomierz analogowy LC-1 przy amplitudzie sygnału 90V.

4. Pomiar częstotliwości oscyloskopem.

1. Z definicji.

d = 4,2 dz - odczytana z ekranu długość odcinka odpowiadającego okresowi

c = 0,1 ms - nastawa przełącznika podstawy czasu

f_N = 1998 Hz

f_x = f_x - f_N = 2380,95 Hz -1998 Hz = 382,95 Hz

2. Metoda krzywych Lissajous.

Wyniki pomiarów.

L.p.	PW -13	PFL-23
		fN	fN	nx	ny	fx
		Hz	Hz	-	-	Hz
1	52	53,4	2	2	53,4
2	520	588,6	2	2	588,6

Przykłady obliczeń.

(w obu przypadkach)

Przykład krzywej Lissajous.

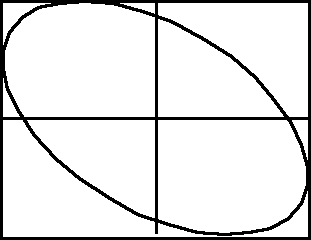
f_x = 53,4 Hz

5. Pomiar przesunięcia fazowego.

1. Z definicji.

Wyniki pomiarów:

	T				δ
L.p.	dz	dz	°	°	%
1	4,7	0,5	38,3	8,5	22,1
2	4,7	3,7	283,4	13,7	4,8
3	2,8	0,32	41,1	14,3	34,9
4	5	4,8	345,6	14,1	4,1

Przykładowe obliczenia:

2. 
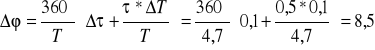
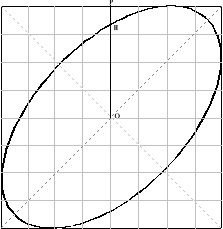
   Metodą krzywych Lissajous.

Wyniki pomiarów:

L.p.	OH	OP			δ
		dz	dz	°	°	%
1	0,4	1,4	16,6	5,7	34,3
2	1,6	1,7	70,3	8,8	12,5
3	2,6	2,6	90,0	8,0	8,9
4	0,9	3,4	15,4	3,2	20,8

Przykładowe obliczenia:

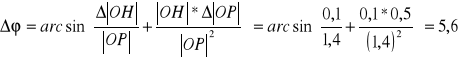
6. Wnioski.

Istnieje wiele metod pomiaru częstotliwości, różniących się od siebie dokładnością , oraz zasadą pomiaru. Podczas wykonywania bezpośrednich pomiarów częstotliwości częstotliwościomierzem cyfrowym zaobserwowaliśmy, że wartość błędu maleje wraz ze wzrostem częstotliwości. Jeżeli mierzymy małą częstotliwość metodą bezpośrednią to powinniśmy dobrać jak największy czas otwarcia bramki, a tym samym zmniejszyć błąd pomiaru. Przy pomiarze pośrednim uzyskujemy przy tej samej dokładności odczytu wartości wynik pomiaru dokładniejszy (dla mniejszych częstotliwości) niż dla metody bezpośredniej. Przy dużych częstotliwościach błąd jest tego samego rzędu, a nawet większy (f >50 kHz).W metodzie pośredniej błąd pomiaru jest tym większy im większa jest częstotliwość mierzona. Dużą dokładność pomiaru uzyskaliśmy również za pomocą miernika analogowego LC-1 o klasie dokładności 0,2. Błąd pomiaru zbliżony był do błędu miernika cyfrowego. Pomiaru częstotliwości można dokonywać również za pomocą oscyloskopu. Wykonuje się to metodą pośrednią przez pomiar długości odcinka odpowiadającego jednemu okresowi i pomnożeniu go przez podstawę czasu. Pomiar ten jest dość dokładny, a jego dokładność zależy od dokładności odczytu długości odcinka odpowiadającego jednemu pełnemu okresowi przebiegu mierzonego (w ćwiczeniu otrzymaliśmy bardzo duży błąd z powodu rozkalibrowania podstawy czasu oscyloskopu). Z kolei metoda krzywych Lissajous nie należy do najdokładniejszych, z tego też względu jest rzadko wykorzystywana (do pomiaru potrzebny jest dodatkowo drugi wzorzec częstotliwości o dużej dokładności i zakresie regulacji częstotliwości - aby uzyskać stabilny obraz na ekranie oscyloskopu)..

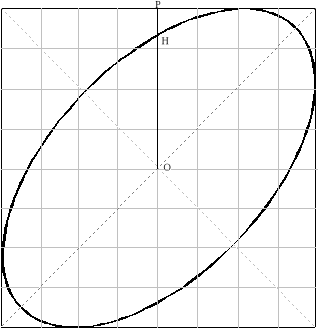
Przy pomiarze przesunięcia fazowego z definicji należy zwrócić uwagę na kalibrację oscyloskopu (w ćwiczeniu była ona włączona i dlatego pomiar jest obarczony dużym błędem). W metodzie krzywych Lissajous dokładność pomiaru nie zależy od ustawień oscyloskopy (pracuje on z wyłączoną podstawą czasu), jednak pomiar jest obarczony dość dużym błędem (>10%). Zastosowana metoda wyznaczania kąta przesunięcia fazowego daje bardzo duże błędy dla przesunięć mniejszych niż 60°- dla takich kątów powinno się liczyć kąt przesunięcia fazowego z zależności :

, gdzie

r - długość minimalna promienia elipsy,

R - długość maksymalna promienia elipsy,

jednak wymaga to określenia długości w kierunkach, w których nie ma podziałki (po przekątnych ekranu), dlatego metodę tą można stosować do zgrubnej oceny wartości przesunięcia fazowego. Dla dokładniejszych wyników należy zastosować mierniki przesunięcia fazowego (cyfrowe lub analogowe).

Przy pomiarach w punkcie 4b częstotliwość generatora PW - 13 była kontrolowana za pomocą częstotliwościomierza z powodu dużej rozbieżności między wskazaniami obu przyrządów - za poprawną przyjęta została wartość częstotliwościomierza cyfrowego PFL - 23.

Duże różnice przesunięć fazowych oraz częstotliwości mierzonych oscyloskopem metodą z definicji a innymi metodami spowodowane są włączeniem kalibracji podstawy czasu w oscyloskopie co spowodowało zmianę wymiarów poziomych obrazu w granicach nawet do 100%. Za wartość poprawną przesunięcia fazowego można uznać wartość otrzymaną w pomiarze metodą krzywych Lissajous ponieważ w czasie wykonywania tych pomiarów podstawa czasu była wyłączona.

---