124	24.03.99	Piotr Górnik	Wydział Elektryczny	semestr IV	grupa A1
	Prowadzący ADAM BUCZEK		Przygotowanie	Wykonanie	Ocena

Temat: Sprawdzenie drugiej zasady dynamiki ruchu obrotowego za pomocą wahadła Oberbecka

1. Podstawy teoretyczne.

Podstawowym równaniem dynamiki w ruchu postępowym jest równanie wyrażające drugą zasadę Newtona:
. W przypadku ruchu obrotowego drugą zasadę dynamiki wyraża się za pomocą momentu bezwładności I oraz przyspieszenia kątowego
. W celu dokonania tego przejścia rozważmy ciało sztywne obracające się wokół osi SS'. Załóżmy, że na to ciało działa siła
przyłożona w punkcie P. W nieskończenie małym przedziale czasu dt punkt P przemieści się o
,tzn. jego promień wodzący zakreśli kąt
. Praca wykonana przez tę siłę:

(1)

Gdyby na ciało sztywne działało więcej sił, to przez
należy rozumieć wypadkowy moment siły względem osi SS'. Po podzieleniu obustronnie wyrażenia (1) przez przedział czasu dt, otrzymamy wzór na moc w ruchu obrotowym:

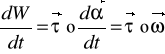
(2)

w którym
oznacza prędkość kątową ciała. Moc w ruchu obrotowym możemy także przedstawić jako przyrost energii kinetycznej ciała w jednostce czasu. Energia kinetyczna związana z obrotem ciała wynosi
. Jeżeli I=const, a oś obrotu jest nieruchoma, to:

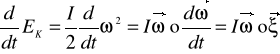
(3)

Z porównania zależności (2) i (3) otrzymujemy, że:

(4)

Powyższe równanie wyraża drugą zasadę dynamiki Newtona dla ruchu obrotowego. Zasadę tę można również zapisać w postaci:

lub
(5)

przy czym
i oznacza moment pędu lub inaczej kręt. W przypadku gdy moment sił działających na ciało
, to
, czyli
. Równanie to wyraża pierwszą zasadę dynamiki Newtona dla ruchu obrotowego, zgodnie z którą ciało sztywne pozostaje w spoczynku lub porusza się ruchem jednostajnym obrotowym, jeżeli moment sił zewnętrznych
.

2. Zasada pomiaru

Ruch obrotowy wahadła Oberbecka wywołuje moment siły o wartości:

(6)

gdzie m oznacza masę ruchomego obciążnika, g - przyspieszenie ziemskie, a r - promień krążka z nawiniętą nicią. Przyspieszenie kątowe wahadła można zapisać w postaci:

(7)

Przyspieszenie liniowe a możemy wyznaczyć z pomiaru wysokości h spadania obciążnika oraz czasu t trwania tego spadku. Ostatecznie:

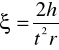
(8)

Druga zasada dynamiki ruchu obrotowego rozważanego wahadła ma postać:

(9)

gdzie I jest całkowitym momentem bezwładności wahadła. Moment ten o postaci:

(10)

jest sumą dwóch składników - I₀ stanowi tę część momentu bezwładności wahadła, która jest niezależna od położenia walców o masach m_W zamocowanych na krzyżaku w odległości d od osi obrotu.

Po podstawieniu zależności (6), (8) i (10) do równania (9) otrzymamy:

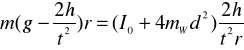
(11)

co można sprowadzić do postaci:

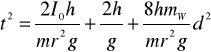
(12)

Po wprowadzeniu oznaczeń:

,
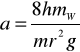
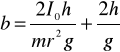
(13)

otrzymamy, że:

(14)

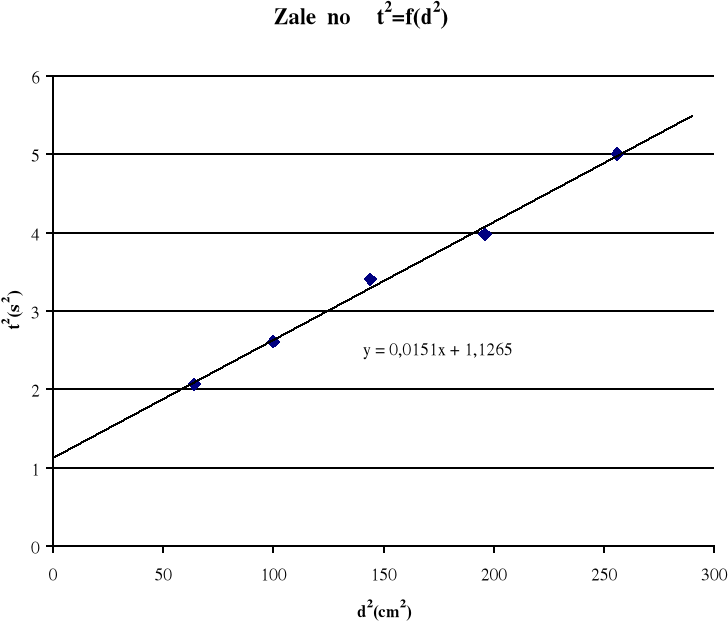
Powyższy związek liniowy między kwadratem czasu spadku obciążnika i kwadratem odległości mas m_{W ­­} od osi obrotu jest równoważny równaniu (9). Gdy wykreślimy funkcję (14) w układzie xy, w którym x=d², y=t², możemy wyznaczyć współczynniki a i b będące odpowiednio współczynnikiem nachylenia prostej i wartością funkcji dla x=0. Wartość współczynnika b po rozwiązaniu zależności (13) pozwala obliczyć moment bezwładności I₀:

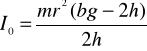
(15)

3. Pomiary

m_W=40±0,1g

r=0,02±0,001m

h=0,47±0,001m

m=5*40±0,1=200±0,5g

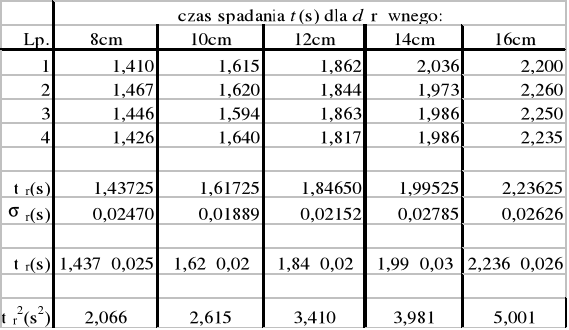
4. Obliczenia

Na podstawie regresji liniowej wyznaczamy parametry:

a=0,0151

b=1,1265

Zgodnie ze wzorem (15):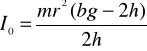
obliczam moment bezwładności ( przyjmuję g=9,81m/s² ):

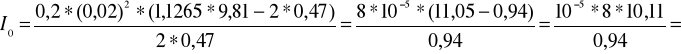
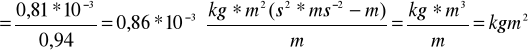
5. Wnioski

Otrzymany przeze mnie wynik wydaje się być prawdopodobny ( m.in. ze względu na dużą dokładność pomiarów i bliską ideałowi liniowość zależności t²=f(d²) ). Trudno jednakże na podstawie tego wyniku wnioskować o prawdziwości drugiej zasady dynamiki, na której to podstawie dokonałem obliczeń. Jest tak dlatego, że nie miałem możliwości obliczenia szukanej wielkości za pomocą alternatywnej, nie opierającej się na powyższym prawie, metody. W tej sytuacji ( w skrypcie nie ma ani słowa na temat sprawdzenia tak otrzymanego wyniku ) tytuł ćwiczenia wydaje się być „nieco dziwny”.

str. 4

str. 1

---