Akademia Techniczno-Humanistyczna
Wydział: Nauk o Materiałach i środowisku
Kierunek: Inżynieria Środowiska
Rok akademicki: 2010/2011
Ćwiczenie nr 56
Badanie wpływu temperatury na opór elektryczny
Przewodników i półprzewodników
Numer grupy laboratoryjnej: 103
Wstęp teoretyczny
1.Opór elektryczny - jest to stosunek napięcia panującego na końcach przewodnika do natężenia prądu przepływającego przez ten przewodnik. Opisuje go wzór:
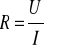
gdzie: U= napięcie, I= natężenie
Jednostką oporu elektrycznego jest 1 om. (1Ω= ![]()
)
2. Prawo Ohma -Natężenie prądu elektrycznego płynącego przez przewodnik jest wprost proporcjonalne do wartości napięcia elektrycznego na jego końcach i odwrotnie proporcjonalne do rezystancji przewodnika. Prawo Ohma wyraża się wzorem:
![]()
3. Przewodnik - to substancja, która dobrze przewodzi prąd elektryczny, a przewodzenie prądu ma charakter elektronowy. Atomy przewodnika tworzą wiązania, w których elektrony walencyjne (jeden, lub więcej) pozostają swobodne (nie związane z żadnym z atomów), tworząc w ten sposób tzw. gaz elektronowy.
4. Półprzewodnik - najczęściej substancje krystaliczne, których konduktywność (przewodnictwo właściwe) może być zmieniana w szerokim zakresie poprzez domieszkowanie, ogrzewanie, oświetlenie bądź inne czynniki. Przewodnictwo typowego półprzewodnika plasuje się między przewodnictwem metali i dielektryków.
Półprzewodniki dzielimy na:
Samoistne - których materiał jest idealnie czysty, bez żadnych zanieczyszczeń struktury krystalicznej
Domieszkowane - to takie, których siatkę krystaliczną wprowadza się odpowiednią ilość innych pierwiastków trój lub pięciowartościowych. Dzielimy je na półprzewodniki typu:
„n”- domieszkami są pierwiastki pięciowartościowe np. fosfor. Półprzewodniki tego typu maja wolne elektrony, nazywamy je donorami
„p” - domieszkami są pierwiastki trójwartościowe np. bor, glin. Półprzewodniki tego typu mają tzw. dziury czyli miejsca na elektron, nazywamy je akceptorami.
5. Dielektryki - czyli izolatory materiał, w którym bardzo słabo przewodzony jest prąd elektryczny. Może to być rezultatem niskiej koncentracji ładunków swobodnych, niskiej ich ruchliwości, lub obu tych czynników równocześnie.
6. Wpływ temperatury na oporność ciał stałych
W półprzewodnikach w miarę wzrostu temperatury zwiększa się energia ruchu cieplnego atomów, dzięki czemu w wyniku zderzeń więcej elektronów może uzyskać energię wystarczającą do przejścia z pasma walencyjnego do pasma przewodnictwa. Tym samym ze wzrostem temperatury zwiększa się liczba generowanych par nośników ładunku: elektron-dziura i maleje opór elektryczny półprzewodnika. Zjawisko ma więc charakter odwrotny niż w przypadku metali, które w tych samych warunkach wykazują wzrost oporu elektrycznego(związane jest to z pojęciem poziomu Fermiego).
W temp. zera bezwzględnego elektrony stopniowo zapełniają kolejne poziomy licząc od podstawowego. Po rozmieszczeniu wszystkich elektronów swobodnych jest sytuacja gdzie pewien poziom energetyczny rozgranicza poziomy całkowicie zapełnione od całkowicie pustych. Ten poziom nazywa się „poziomem Fermiego”. Pod wpływem temp. tylko nieliczne elektrony, te znajdujące się zaraz pod poziomem Fermiego, potrafią przeskoczyć do pasma przewodnictwa i być odpowiedzialne za przewodnictwo cieplne i elektryczne przewodników (dlatego m.in. opór przewodników rośnie ze wzrostem temp.).
7. Zależność oporu elektrycznego od temperatury dle metali opisuje równanie:
R R (1 t
gdzie: R - opór elektryczny przewodnika w temperaturze t
R0 - opór elektryczny przewodnika w temperaturze t0 = 0oC
- temperaturowy współczynnik oporu elektrycznego
Zależność oporu elektrycznego od temperatury dla półprzewodników opisuje równanie:
![]()
R R p 0 e
gdzie: R - wartosc oporu elektrycznego w temperaturze T, wyra_onej w skali bezwzglednej.
Rp0 - stała zale_na od koncentracji nosników ładunku w stanie podstawowym i ich
ruchliwosci w danym półprzewodniku.
E - szerokosc pasma wzbronionego,
k - stała Boltzmanna (k = 1,3810-23 J/K)
II. Tabele z wynikami pomiarowymi i obliczeniami
Tab.1
Nr pomiaru |
przewodnik |
półprzewodnik |
||
|
t [oC] |
R [Ω] |
t [oC] |
R [kΩ] |
1 |
22 |
17.76 |
22 |
9.571 |
2 |
25 |
17.94 |
25 |
8.256 |
3 |
30 |
18.26 |
30 |
6.561 |
4 |
35 |
18.60 |
35 |
5.230 |
5 |
40 |
18.95 |
40 |
4.197 |
6 |
45 |
19.31 |
45 |
3.414 |
7 |
50 |
19.67 |
50 |
2.801 |
8 |
55 |
20.03 |
55 |
2.339 |
9 |
60 |
20.40 |
60 |
1.957 |
10 |
65 |
20.78 |
65 |
1.647 |
11 |
70 |
21.17 |
70 |
1.387 |
12 |
75 |
21.58 |
75 |
1.199 |
13 |
80 |
22.00 |
80 |
1.039 |
Tab.2
Nr pomiaru |
przewodnik |
półprzewodnik |
|||||
|
t [oC] |
R [Ω] |
T [K] |
1/T [K-1] |
R [k Ω] |
lnR |
Rt [k Ω] |
1 |
22 |
17.76 |
295.15 |
33.88* 10 -4 |
9.571 |
9.166 |
9.482 |
2 |
25 |
17.94 |
298.15 |
33.54* 10 -4 |
8.256 |
9.019 |
8.326 |
3 |
30 |
18.26 |
303.15 |
32.99* 10 -4 |
6.561 |
8.789 |
6.615 |
4 |
35 |
18.60 |
308.15 |
32.45* 10 -4 |
5.230 |
8.562 |
5.362 |
5 |
40 |
18.95 |
313.15 |
31.93* 10 -4 |
4.197 |
8.342 |
4.346 |
6 |
45 |
19.31 |
318.15 |
31.43* 10 -4 |
3.414 |
8.136 |
3.558 |
7 |
50 |
19.67 |
323.15 |
30.95* 10 -4 |
2.801 |
7.938 |
2.942 |
8 |
55 |
20.03 |
328.15 |
30.47* 10 -4 |
2.339 |
7.757 |
2.433 |
9 |
60 |
20.40 |
333.15 |
30.02* 10 -4 |
1.957 |
7.579 |
2.013 |
10 |
65 |
20.78 |
338.15 |
29.57* 10 -4 |
1.647 |
7.407 |
1.698 |
11 |
70 |
21.17 |
343.15 |
29.14* 10 -4 |
1.387 |
7.235 |
1.418 |
12 |
75 |
21.58 |
348.15 |
28.72* 10 -4 |
1.199 |
7.089 |
1.209 |
13 |
80 |
22.00 |
353.15 |
28.32* 10 -4 |
1.039 |
6.946 |
1.020 |
Przewodnik |
Półprzewodnik |
||||||
a= 0.07291 [ K-1 ] Δa= 0.00081 [K-1] b= 16.07 [Ω] Δb= 0,04 [Ω] |
a= 4009 [ K ] Δa= 32 [ K ] b= -4.443 [Ω] Δb= 0.099 [Ω] |
||||||
Obliczenia dla półprzewdonika
Przeliczenie stopni Celsjusza na Kelvina t[oC] T [K]
T [K] = t [°C ] + 273.15
T [K] = 22 0C + 273.15 = 295.15 [K]
![]()
= ![]()
= 33.88 * 10 -4 [K-1]
lnR = ln 9571 = 9.166
Teoretyczna wartość oporu elektrycznego półprzewodnika Rt (dla 295.15 [K])
ln R = ![]()
![]()
+ ln Rpo
gdzie:
y = ln R
a =![]()
x = ![]()
b = ln Rpo, => Rpo= eb
![]()
![]()
Rt = Rpo e = eb e
![]()
Rpo= e -4.443 = 0.012
=![]()
= 13.58
![]()
![]()
e =e = e 13.58 = 790167.32
Rt = e -4.443 e 13.58 = 0.012 790167.32 = 9482.0078 [Ω] => 9.482 [k Ω]
Tab. 3
Przewodnik |
Półprzewodnik |
||
R0 ± ΔR0 [Ω] |
α ± Δα 10-3[ K ]
|
Rp0 ± ΔRpo [Ω] |
E ± ΔE [eV] |
16.07 ± 0.04 |
4.54 ± 0.61 |
0.0116 ± 0.0012 |
0.3457 ± 0.0027 |
Opór elektryczny przewodnika Ro w to=0oC oraz błąd bezwzględny oporu ΔR0
Ro = 16.07 Ro = b
ΔRo= 0.04 ΔR0 = Δb
Wartość β oraz błąd tej wartości Δβ
β = 0.07291 β= a
Δβ= 0.00081 Δβ= Δa
Wartość temperaturowego współczynnika oporu elektrycznego przewodnika oraz błąd bezwzględny współczynnika
![]()
=![]()
= 0.00454
![]()
= ![]()
=0.011
![]()
=![]()
= 0.0025
Δα = ![]()
![]()
|![]()
| + |![]()
|)
Δα=![]()
(|![]()
| + |![]()
|)= 0.0045 (0.011+0.0025)= 0.00061
Wartość stałej Rp0 oraz jej błąd bezwzględny Δ Rp0
Rp0 = eb = e -4.443 = 0.0116
Δ Rp0 = eb Δb = e -4.443 0.099= 0.012 0.099= 0.0012
Szerokość pasma wzbronionego w półprzewodniku E oraz błąd bezwzględny E
szerokości pasma wzbronionego
E= ak k= 1,3810-23 J
E = ![]()
=0.3457 [eV]
ΔE= Δa k
ΔE= ![]()
= 2.7 [eV]
Sporządziliśmy wykresy:
R= f(t) dla przewodnika
lnR = f(1/T) dla półprzewodnika
R = f(T) i Rt = f(T) dla półprzewodnika
III. Wnioski
Dzięki temu doświadczeniu można stwierdzić, że opór zależy od temperatury. Im większa temperatura tym większy jest opór przewodników a w przypadku półprzewodników opór maleje wraz ze wzrostem temperatury.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
56?danie wpływu temperatury na przewodnictwo elektryczne przewodników i półprzewodników (2)
40 Zastosowanie metody Stokesa do badania wpływów temperatury na lepkość cieczy, Sprawozdania ATH
Badanie wpływu temperatury na rezystancję przewodników i półprzewodników
8 Badanie wpływu genu na występowanie choroby
badanie wpływu rozpuszczalnika na wklanizacje fizyko
Badanie wpływu zagęszczenia na żywotność osobników populacji patyczaków, referaty i materiały, biolo
Badanie wpływu napięcia na natężenie prądu
ćw.10.Badanie właściwości łuku prądu stałego, Elektrotechnika - notatki, sprawozdania, Urządzenia el
Wpływ cisnienia i temp na wytrzymalosc elektryczna powietrza
Wpływ cisnienia i temp na wytrzymalosc elektryczna powietrza, Technika Wysokich Napięć, TWN Labo, L
ćw.10.Badanie właściwości łuku prądu stałego, Elektrotechnika - notatki, sprawozdania, Urządzenia el
cw 52A - Badanie charakterystyk transformatora, Sprawozdania jakieś, Fizyka [na chemii]
Badanie wpływu rozruchu bezoporowego i hamowania rekuperacyjnego na zużycie energii
badanie zaleźności temp oporu półprzewodnika, Politechnika Opolska, 2 semestr, Fizyka - Laboratorium
cw.91 - Badanie zewn©trznego zjawiska fotoelektrycznego, EDUCATION, PWR, FizykaLab
Modulacja i detekcja, 6.3.3. ab, BADANIE WPŁYWU AMPLITUD SYGNAŁÓW NA PROCES MODULACJI AM
BADANIA FIZYKALNE-cw 1i2
więcej podobnych podstron