![]()
jest funkcją jednorodną, jeżeli spełniona jest zależność:
Fazy wieloskładnikowe (roztwory)
Układ i otoczenie
Układ to część wszechświata, którą wybraliśmy do badania. Pozostała część wszechświata to otoczenie. Układ, w którym biegną jakieś reakcje chemiczne to układ chemiczny.
Faza
Faza to część układu o wyraźnych granicach z nieciągłą zmianą jakichś parametrów makroskopowych. Faza może być jednolita (w jej wnętrzu nie obserwujemy żadnych zmian makroskopowych) lub niejednolita (obserwujemy w niej ciągła zmianę jakichś parametrów makroskopowych).
Składniki niezależne
Te różne substancje chemiczne, których znajomość (znajomość rodzaju i ilości) jest konieczna i wystarczająca do pełnego określenia stanu fazy. W celu znalezienia liczby składników niezależnych można posłużyć się intuicja chemiczną lub wzorem: λ = l - w; gdzie λ - liczba składników niezależnych, l - liczba wszystkich składników, w - liczba więzów narzuconych na układ.
Twierdzenie Eulera
![]()
jest funkcją jednorodną, jeżeli spełniona jest zależność:
![]()
gdzie: m - rząd funkcji
k - dowolna liczba rzeczywista
x - składniki niezależne
Dla każdej funkcji jednorodnych spełnione jest twierdzenie Eulera o funkcjach jednorodnych:
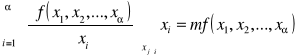
II twierdzenie Eulera:
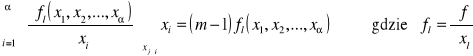
Zastosowanie twierdzenia Eulera
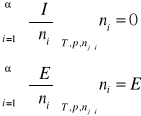
Wielkości intensywne
Nie zależą od globalnej masy fazy - T, p, d. Są funkcjami jednorodnymi rzędu zerowego liczb moli składników niezależnych.
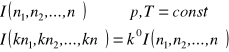
Funkcje ekstensywne
Zależą od masy fazy - V, U, H, S, F, G. Są funkcjami jednorodnymi rzędu pierwszego liczb moli składników niezależnych.
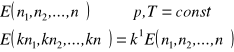
Wielkości parcjalne (cząstkowe)
Molowa wielkość parcjalna (cząstkowa) jest to pochodna cząstkowa dowolnej wielkości ekstensywnej E względem liczby moli danego składnika niezależnego ni, przy stałych T i p i stałych liczbach moli pozostałych składników niezależnych nj≠i.
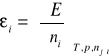
Sens fizyczny molowej wielkości parcjalnej:
Wyraża ona zmianę wartości danej funkcji ekstensywnej w wyniku wprowadzenia do fazy, przy stałych T i p oraz przy stałym składzie, jednego mola i-tego składnika.
Każda wielkość parcjalna jest wielkością intensywną. Wielkości parcjalnej nie można utożsamiać z czystym składnikiem, zależy ona od T, p i składu.
Potencjał chemiczny
Potencjał chemiczny danego składnika w fazie wieloskładnikowej jest pochodną cząstkową potencjału termodynamicznego względem liczby moli tego składnika przy stałych parametrach fizycznych charakterystycznych dla potencjału termodynamicznego oraz przy stałych liczbach moli pozostałych składników niezależnych.
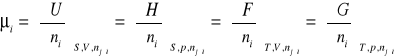
Potencjał chemiczny μi i-tego składnika jest molową parcjalną entalpią swobodną tego składnika: ![]()
. Jest zatem wielkością intensywną, ma więc określona wartość w każdym miejscu fazy i nie zależy od jej globalnej masy, a jedynie od jej stanu wewnętrznego.
Równanie Gibbsa-Duhema
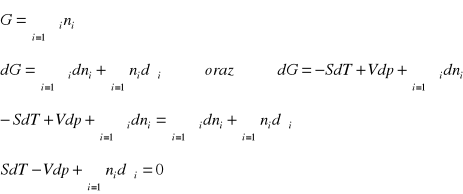
Równanie Gibbsa-Duhema wiąże w jedną zależność zmiany dT, dp i dμi, a zatem zmiany wielkości intensywnych fazy znajdującej się w stanie równowagi. Liczba niezależnych ich zmian jest więc o jeden mniejsza od ogólnej ich liczby.
(musimy znać α+1 zmiennych niezależnych [wartości intensywnych], a nie α+2 - ilość składników niezależnych plus temperatura i ciśnienie)
Funkcje standardowe i funkcje mieszania
Każda wielkość parcjalna jest wielkością intensywną, dogodnie jest ją wyrażać jako funkcję samych tylko wielkości intensywnych, np. temperatury, ciśnienia i stężeń poszczególnych składników. Stężeń niezależnych jest tylko α-1 (gdy stężenie wyrazimy ułamkiem molowym).
Molową parcjalną wielkość intensywną można wyrazić jako funkcję T, p i xi:
![]()
Każdą funkcję T, p, xi można wyrazić za pomocą dwu funkcji:
- funkcji standardowej - zależnej tylko od T i p; oznaczanej symbolem θ
- funkcji mieszania - zależnej od T, p, xi; oznaczanej indeksem m
![]()
Stosując powyższe równanie do molowej parcjalnej entalpii swobodnej, czyli potencjału chemicznego, otrzymujemy:
![]()
Funkcję ![]()
można zastąpić funkcją ![]()
noszącą nazwę molowej aktywności składnika i :
![]()
Funkcja ![]()
nosi nazwę współczynnika aktywności składnika i :
![]()
Potencjał chemiczny wyrażony za pomocą aktywności:
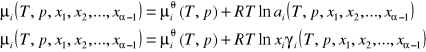
Termodynamiczna klasyfikacja roztworów
Do klasyfikacji roztworów korzystamy z równania:
![]()
|
|
γi = 1 |
|
|
|
|
nie spełnione |
||
roztwór idealny
|
|
roztwór nieidealny |
||
zał: |
|
|
|
|
spełnione |
nie spełnione |
|
||
|
|
|
||
roztwór idealny doskonały
|
roztwór idealny niedoskonały |
|
||
Roztwór idealny - jeśli składa się z samych faz idealnych (γi = 1 ⇒ ai = xi)
Roztwór idealny doskonały - idealny z całym zakresie stężeń
Roztwór idealny niedoskonały - idealny tylko w pewnym zakresie stężeń
Roztwór nieidealny - gdy choć dla jednego składnika γi ≠ 1
Wybór układu odniesienia
Wyboru układu odniesienia dokonujemy w celu wyznaczenia współczynników aktywności.
Symetryczny układ odniesienia
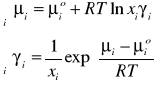
Niesymetryczny układ odniesienia
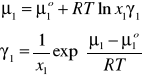
Składnik numer 1 jest rozpuszczalnikiem i dominuje w roztworze. Przyjmujemy dla niego ![]()
. Dla pozostałych składników mamy:
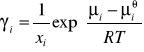
Układy wielofazowe
Reguła faz Gibbsa
Stan układu α-składnikowego i β-fazowego określają zmienne intensywne: T, p, stężenie (α-1) składników niezależnych każdej z faz. Dla całego układu zmiennych niezależnych jest β(α-1) → w każdej z faz, których jest β, jest (α-1) składników niezależnych. Wszystkich zmiennych intensywnych będzie: β(α-1) + T + p = β(α-1) + 2
W układzie zbudowanym z α składników niezależnych występuje β faz. Warunkiem izotermiczno-izobarycznej równowagi fazowej jest, aby dla każdego składnika z osobna potencjały chemiczne we wszystkich fazach były jednakowe: μij = μik, co można zapisać równaniami:
μ11 = μ12 = ... = μ1β
μ21 = μ22 = ... = μ2β stężeń tych jest α(β-1)
Dla zredukowania stanu równowagi przyrównujemy:
β(α-1) + 2 = α(β-1) → s = α - β + 2
Różnica s między tymi liczbami nosi nazwę liczby stopni swobody. Określa ona, ile zmiennych intensywnych można niezależnie zmienić, nie powodując przy tym zmiany stanu równowagi w układzie.
s = α - β + 2 reguła faz Gibbsa
s - liczba stopni swobody
α - składniki
β - fazy
Równanie Clausiusa-Clapeyrona
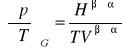
Hβ→α - różnica entalpii spowodowana przejściem fazy β do α
Vβ→α - różnica objętości spowodowana przejściem fazy β do α
Równanie to opisuje przejście fazowe wzdłuż linii równowagi między dowolnymi fazami (parowanie, topnienie, sublimacja, przejścia między różnymi postaciami krystalicznymi). Pozwala na wyznaczenie nachylenia krzywych na diagramach fazowych.
Reguła Troutona
Entropia parowania jest stała dla większości cieczy i wynosi około 88 J/(K⋅mol).
ΔSpar. = ΔHpar ./ Tw
ΔSpar. - entropia parowania
ΔHpar - molowe ciepło parowania
Tw - normalna temperatura wrzenia
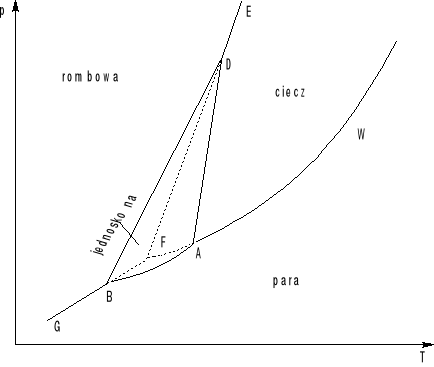
Układ enancjotropowy
Układ enancjotropowy to taki układ, w którym istnieje trwały punkt potrójny między dwoma fazami stałymi i parą. Na diagramie fazowym siarki jest to punkt B.
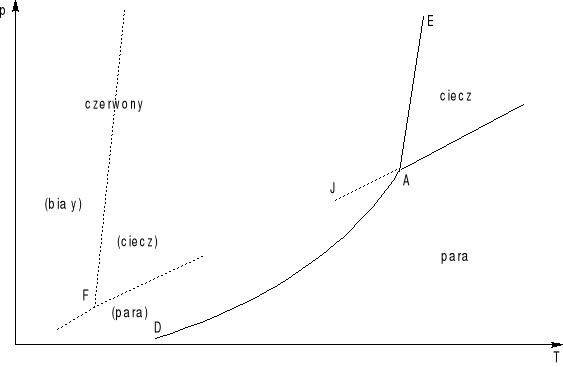
Układ monotropowy
Układ monotropowy to taki układ, w którym brak punktu równowagi między dwiema fazami stałymi i parą. Rysunek przedstawia diagram fazowy fosforu.
Pojemność cieplna w stałej objętości
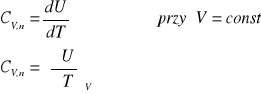
Pochodną energii względem temperatury przy stałej objętości nazywamy pojemnością cieplną w stałej objętości.
Pojemność cieplną przypadającą na 1 mol, czyli molową pojemność cieplną, nazywamy krótko ciepłem molowym.
CV = CV,n / n
Pojemność cieplna pod stałym ciśnieniem
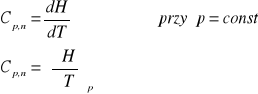
Pochodną entalpii względem temperatury przy stałym ciśnieniu nazywamy pojemnością cieplną pod stałym ciśnieniem.
Iloraz pojemności cieplnej przez liczbę moli (n), nazywamy ciepłem molowym pod stałym ciśnieniem.
Cp = Cp,n / n
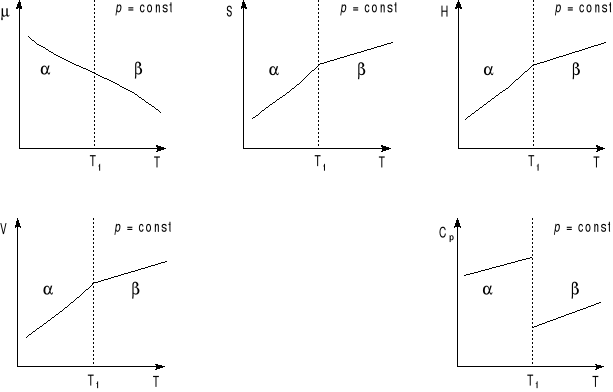
Przemiany fazowe I rodzaju
Przemiany fazowe, których pierwsze pochodne potencjału chemicznego są nieciągłe nazywa się przemianami pierwszego rodzaju. Są to np. topnienie, wrzenie, sublimacja, przemiany polimorficzne.
Potencjały chemiczne μα i μβ są malejącymi funkcjami temperatury o krzywiźnie ujemnej, są więc krzywymi wypukłymi. W temperaturze przemiany fazowej Tf obie fazy współistnieją w równowadze: μα = μβ. W temperaturach różnych od Tf trwała jest faza o mniejszym potencjale. Przed przejściem fazowym μα < μβ.
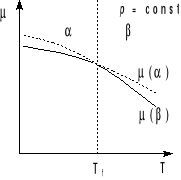

W temperaturze przejścia fazowego Tf potencjał chemiczny zmienia się w sposób ciągły, natomiast jego pierwsze pochodne zmieniają się skokowo, bo pochodna ∂μ/∂T nie istnieje.
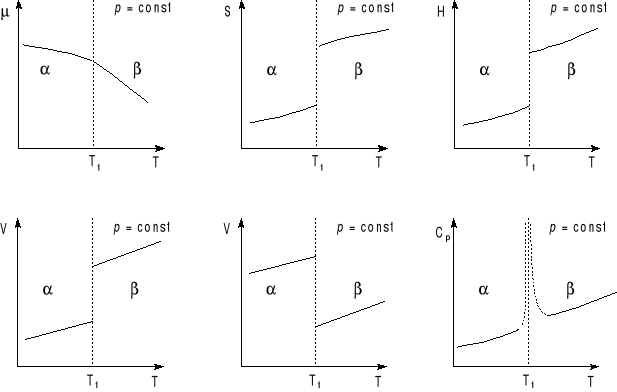
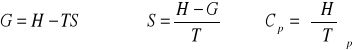
Przemiany fazowe II rodzaju
Przemiany fazowe, w których druga pochodna potencjału jest nieciągła. Przykładem tych przemian może być przejście ferromagnetyku i paramagnetyk, przejście helu ciekłego w nadciekły (lepkość cieczy nadciekłej taka jak mają gazy, czyli bardzo niska)
Prawo Raoulta
Badamy związek pomiędzy składem roztworu doskonałego a jego prężnością pary. Potencjał chemiczny składnika w każdej fazie jest funkcją temperatury, ciśnienia i ułamka molowego. Ułamiki molowe w fazie gazowej oznaczamy yi. W stanie równowagi potencjały w oby fazach są sobie równe. Dla roztworu i pary zapisujemy równanie:
![]()
Jeżeli czysta ciecz 1 jest w danej temperaturze w równowadze z parą nasyconą, której prężność wynosi p1⊕ to:
![]()
Odejmujemy stronami powyższe równania:
![]()
p1 - prężność cząstkowa
p1⊕ - prężność nad czystym składnikiem
Założenia:
1. Roztwór jest roztworem doskonałym
![]()
2. Para nad roztworem jest doskonałą mieszaniną gazów doskonałych
![]()
3. Para nad czystą cieczą jest gazem doskonałym
![]()
ciśnienie standardowe po = 1 atm; p1 = py1
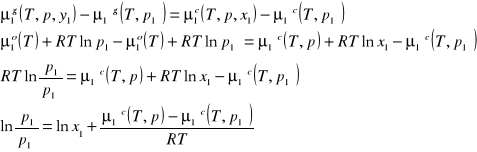
4. Potencjał chemiczny cieczy nie zależy od ciśnienia
![]()
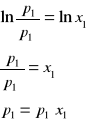
W układzie złożonym z roztworu idealnego rozcieńczonego i pary nad tym roztworem zachowującej się jak gaz doskonały prawo Raoulta stosuje się do rozpuszczalnika, a prawo Henry'ego do substancji rozpuszczonej.
Z prawa Raoulta wynika, że w stałej temperaturze ciśnienia cząstkowe składników nad roztworem doskonałym, jak również całkowite ciśnienie pary nad roztworem są liniowymi funkcjami ułamków molowych w roztworze.
Dla układów nieidealnych prawo Raoulta przyjmuje postać:
![]()
Jeżeli γ > 1 wówczas mamy dodatnie odchylenie od prawa Raoulta, gdy γ < 1, wtedy mamy ujemne odchylenie od prawa Raoulta.
Prawo Henry'ego
![]()
![]()
potencjał chemiczny składnika 1 w fazie ciekłej
![]()
potencjał chemiczny w fazie 2
W równowadze ![]()
otrzymujemy:
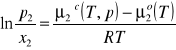
Jeżeli założymy, że potencjał standardowy cieczy nie zależy od ciśnienia prawa strona równania będzie funkcją temperatury:
![]()
Możemy zapisać równanie:
![]()
8
1