Całka różniczki zupełnej.

Niech D - obszar jednospójny,

.

Pytamy czy w obszarze D
, aby wyrażenie

było różniczką zupełną funkcji U w D ?

Oczywiście musi zachodzić
i
.

Wtedy

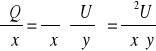
Z założenia

Zatem warunkiem koniecznym istnienia funkcji U jest równość

.

Stwierdzenie

Niech D - obszar jednospójny,

.

Wtedy

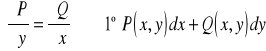
, jest różniczką zupełną funkcji U,

ponadto:

, gdzie
,

- ustalony punkt

- punkt zmienny,

- krzywa regularna,
,

czyli

. (*)

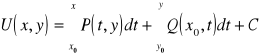
dla dowolnej krzywej
.

Uzasadnienie wzoru (*)

Dla

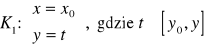
mamy
.

Podobnie dla

otrzymujemy
.

Stąd

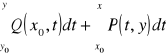
na podstawie twierdzenia o niezależności całki krzywoliniowej od kształtu drogi całkowania. Zatem

.

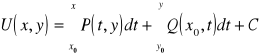
Uwaga

Wektor
jest gradientem funkcji U,
.

Definicja

Funkcję U nazywamy potencjałem pola wektorowego W.

Przykład

Wykazać, że
jest różniczką zupełną pewnej funkcji
i wyznaczyć tę funkcję (potencjał).

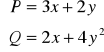
oraz
.

.

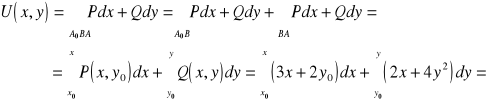
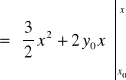
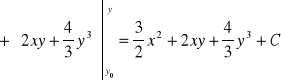
14

---