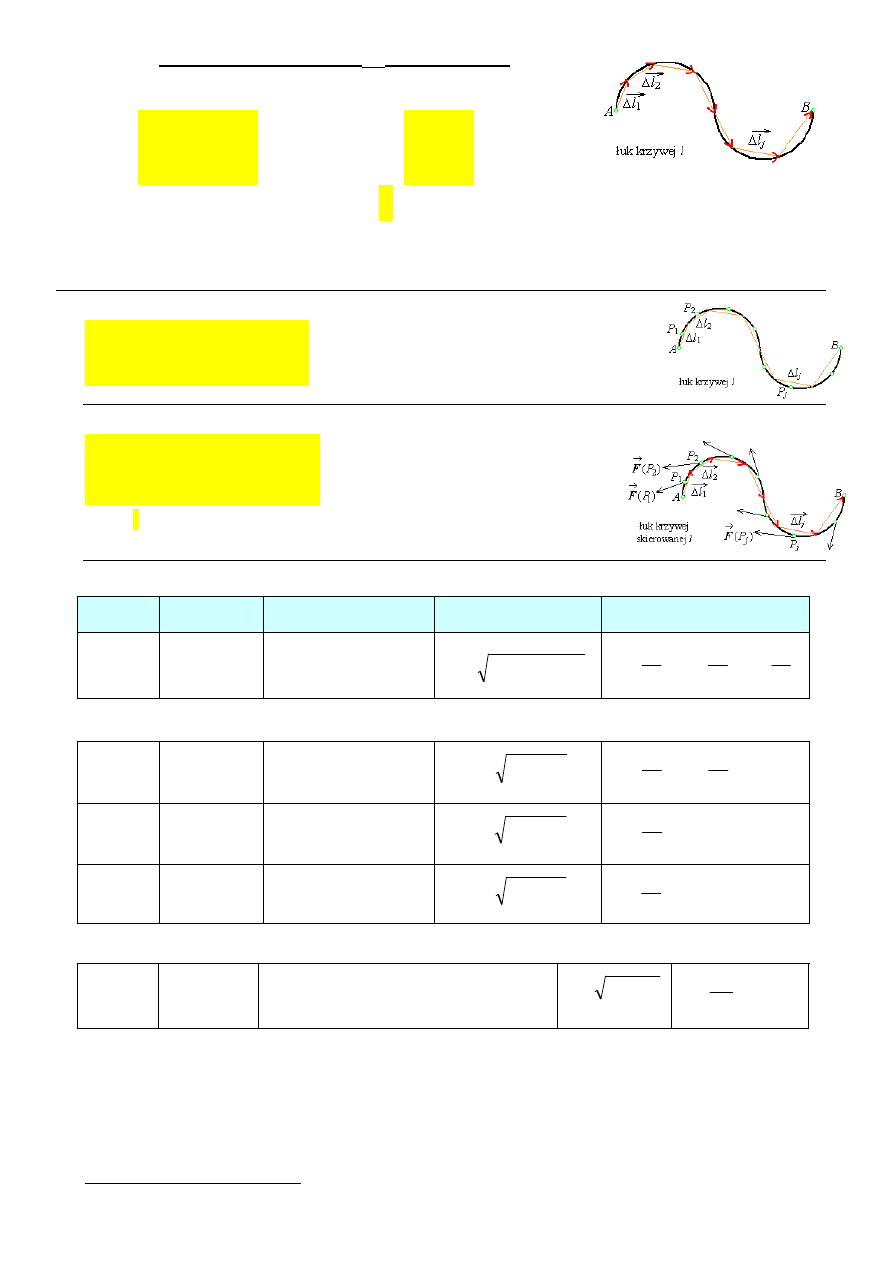
Opracował i wykonał: Stanisław Zoń
1
Wektorowa różniczka
→
l
d
długości łuku
krzywej skierowanej we współrzędnych kartezjańskich
t
z
y
x
d
]
d
,
d
,
d
[
d
⋅
=
=
→
→
v
l
i jej moduł
t
v
l
d
d
⋅
=
.
gdzie:
→
v – wektor styczny do łuku krzywej l . Łuk ma końce w punktach A i B.
d
x, dy, dz – różniczki współrzędnych x, y, z w równaniu łuku:
)
(t
x
x
=
,
)
(t
y
y
=
,
)
(t
z
z
=
,
t – zmienna w równaniu łuku, t
A
, t
B
– wartości t w punktach A i B. Dowolny punkt
)
,
,
(
z
y
x
P
=
.
Całka krzywoliniowa niezorientowana (nieskierowana)
1
∑
=
→
∆
⋅
=
⋅
∫
n
j
j
j
l
l
P
f
l
P
f
1
0
)
(
lim
d
)
(
def
λ
,
∫
⋅
AB
l
l
P
f
d
)
(
( )
∫
⋅
=
A
B
B
A
t
t
t
t
t
v
t
P
f
lub
lub
d
)
(
.
Całka krzywoliniowa zorientowana (skierowana)
A
∑
=
→
→
→
→
→
=
∫
n
j
j
j
l
P
P
1
0
)
(
lim
d
)
(
def
∆l
F
F
o
o
λ
l
∫
→
→
AB
l
l
d
o
F
∫
→
→
=
B
A
t
t
t
d
v
o
F
,
gdzie: º oznacza iloczyn skalarny wektorów.
W obu całkach po prawej stronie są już zwykłe całki oznaczone.
Przypadek
łuku krzywej przestrzennej,
)
,
,
(
z
y
x
P
=
A
Równanie
łuku l
Różniczka
łuku
Wektor styczny
do łuku
Moduł wektora
stycznego do łuku
Objaśnienia
)
(
)
(
)
(
t
z
z
t
y
y
t
x
x
=
=
=
t
d
d
⋅
=
→
→
v
l
t
v
l
d
d
⋅
=
[
]
z
y
x
&
&
&
,
,
=
→
v
2
2
2
z
y
x
v
&
&
&
+
+
=
t
x
x
d
d
=
&
,
t
y
y
d
d
=
&
,
t
z
z
d
d
=
&
Przypadek
łuku krzywej płaskiej w płaszczyźnie Oxy,
)
,
(
y
x
P
=
)
(
)
(
t
y
y
t
x
x
=
=
t
d
d
⋅
=
→
→
v
l
t
v
l
d
d
⋅
=
[ ]
y
x &
&,
=
→
v
2
2
y
x
v
&
&
+
=
t
x
x
d
d
=
&
,
t
y
y
d
d
=
&
(2)
)
(x
y
y
=
x
d
d
⋅
=
→
→
v
l
x
v
l
d
d
⋅
=
[
]
)
(
,
1
'
x
y
=
→
v
2
)
(
1
'
y
v
+
=
x
y
y
d
d
'
=
(3)
)
( y
x
x
=
y
d
d
⋅
=
→
→
v
l
y
v
l
d
d
⋅
=
[
]
1
),
(
'
y
x
=
→
v
2
)
(
1
'
x
v
+
=
y
x
x
d
d
'
=
(4)
Przypadek
łuku krzywej płaskiej we współrzędnych biegunowych (*)
)
(
ϕ
r
r
=
ϕ
d
d
⋅
=
→
→
v
l
ϕ
d
d
⋅
=
v
l
[
]
)
cos(
)
sin(
),
sin(
)
cos(
ϕ
ϕ
ϕ
ϕ
r
r
r
r
+
−
=
→
&
&
v
2
2
r
v
r
+
=
&
ϕ
d
dr
r
=
&
(5)
(*) Wpierw użyto wzorów przejścia do współrzędnych kartezjańskich:
⋅
=
⋅
=
)
sin(
)
(
)
cos(
)
(
ϕ
ϕ
ϕ
ϕ
r
y
r
x
,
a potem wzorów (2) na postać parametryczną. Tu parametrem jest
ϕ
.
Identyczne wzory stosuje się dla łuków krzywych płaskich w płaszczyznach Oyz i Oxz.
1
W całkach krzywoliniowych nieskierowanych za dolną granicę całkowania zawsze podstawiamy mniejszą z liczb.
Opracował i wykonał: Stanisław Zoń
2
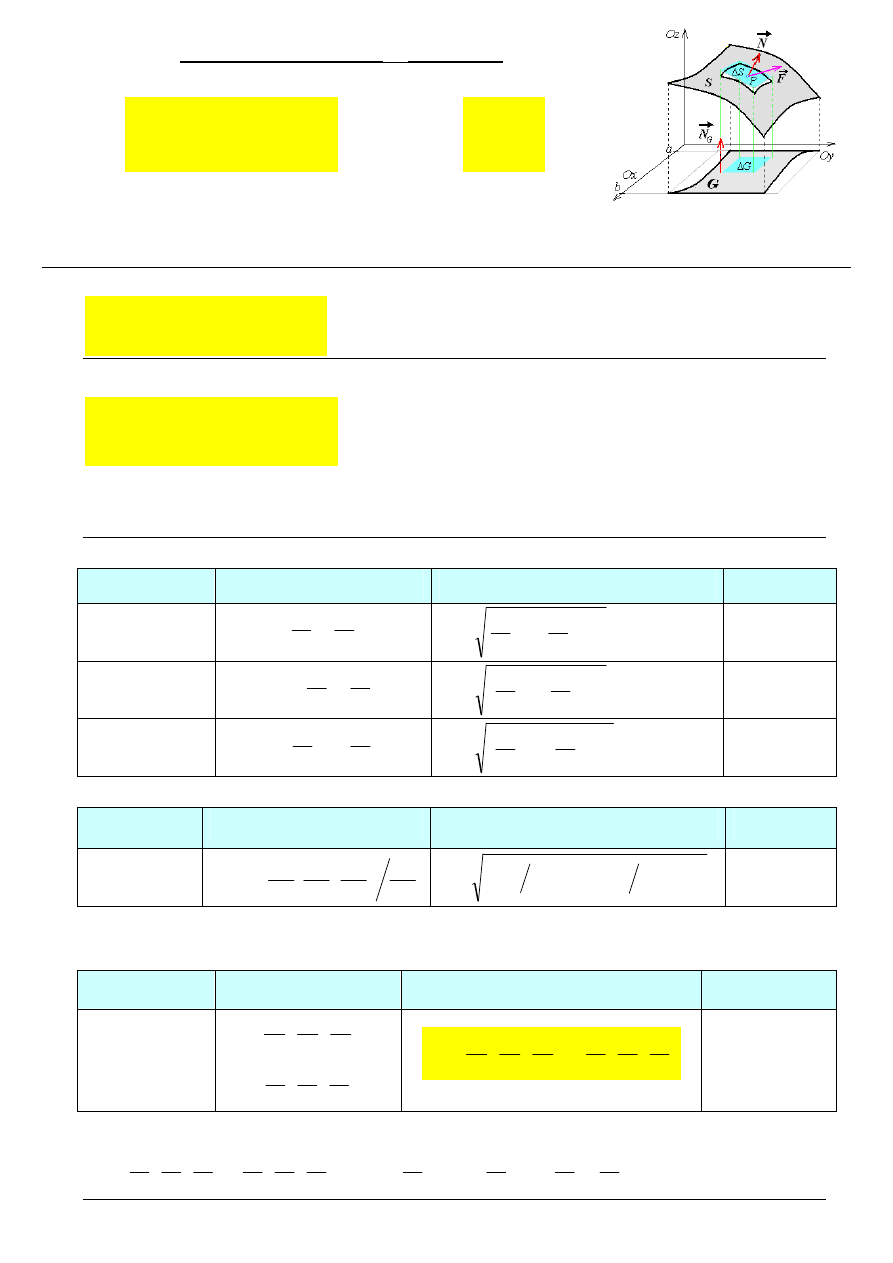
Wektorowa różniczka
→
S
d
pola płata
powierzchni skierowanej we współrzędnych kartezjańskich
G
y
x
x
z
z
y
d
]
d
d
,
d
d
,
d
d
[
d
→
→
=
⋅
⋅
⋅
=
N
S
i jej moduł
G
N
S
d
d
=
,
gdzie:
→
N
– wektor prostopadły do płata powierzchni S,
G – obszar płaski, który jest rzutem płata S na jedną z płaszczyzn układu współrzędnych,
dG – różniczka pola na płaszczyźnie rzutu płata S,
y
x
G
d
d
d
⋅
=
lub
z
x
G
d
d
d
⋅
=
lub
z
y
G
d
d
d
⋅
=
.
Całka powierzchniowa niezorientowana (nieskierowana) w polu skalarnym
)
,
,
(
)
(
z
y
x
f
P
f
=
∑
=
→
∆
⋅
=
⋅
∫∫
n
j
j
j
S
S
P
f
S
P
f
1
0
)
(
)
(
lim
d
)
(
def
λ
,
∫∫
⋅
S
d
)
(
S
P
f
∫∫
⋅
=
G
G
N
P
f
d
)
(
.
Całka powierzchniowa zorientowana (skierowana) w polu wektorowym
)]
(
),
(
),
(
[
)
(
P
Z
P
Y
P
X
P
=
→
F
∑
=
→
→
→
→
→
=
∫∫
n
j
j
j
S
P
P
1
0
)
(
)
(
lim
d
)
(
def
∆S
F
S
F
o
o
λ
,
∫∫
→
→
S
S
F d
o
G
G
d
→
→
∫∫
=
N
F o
.
Uwaga: º oznacza iloczyn skalarny wektorów.
Całki po prawej stronie to zwykłe całki podwójne.
Jeśli płat S można opisać równaniem (6)
)
,
(
y
x
z
z
=
, to w funkcji podcałkowej trzeba to pod-
stawić w miejsce z. Wtedy też różniczka pola
y
x
G
d
d
d
⋅
=
(
patrz tabela poniżej
).
Przypadek
płata powierzchni S danego w postaci jawnej
Równanie
płata powierzchni S
Wektor
prostopadły do S
Moduł wektora
prostopadłego do S
Różniczka pola
dG
)
,
(
y
x
z
z
=
(6)
∂
∂
−
∂
∂
−
±
=
→
1
,
,
y
z
x
z
N
( )
1
2
2
+
∂
∂
+
∂
∂
=
y
z
x
z
N
y
x
G
d
d
d
⋅
=
)
,
(
z
y
x
x
=
(7)
∂
∂
−
∂
∂
−
±
=
→
z
x
y
x ,
,
1
N
( )
1
2
2
+
∂
∂
+
∂
∂
=
z
x
y
x
N
z
y
G
d
d
d
⋅
=
)
,
(
z
x
y
y
=
(8)
∂
∂
−
∂
∂
−
±
=
→
z
y
x
y
,
1
,
N
1
2
2
+
∂
∂
+
∂
∂
=
z
y
x
y
N
z
x
G
d
d
d
⋅
=
Przypadek
płata powierzchni S danego w postaci uwikłanej
Równanie
płata S
Wektor
prostopadły do S
Moduł wektora
prostopadłego do S
Różniczka pola
dG
0
)
,
,
(
=
z
y
x
H
gdy
0
/
≠
∂
∂
z
H
z
H
z
H
y
H
x
H
∂
∂
∂
∂
∂
∂
∂
∂
±
=
→
,
,
N
1
'
'
'
'
2
,
,
2
,
,
+
+
=
z
y
z
x
H
H
H
H
N
y
x
G
d
d
d
⋅
=
Podobne wzory zachodzą dla przypadków
0
/
≠
∂
∂
x
H
oraz
0
/
≠
∂
∂
y
H
.
Przypadek
płata powierzchni S danego w postaci parametrycznej
Równanie
płata powierzchni S
Wektory styczne do S
(niekolinearne)
Wektor
prostopadły do S
Różniczka pola
Ω
d
)
,
( v
u
x
x
=
)
,
( v
u
y
y
=
)
,
( v
u
z
z
=
∂
∂
∂
∂
∂
∂
u
z
u
y
u
x
,
,
∂
∂
∂
∂
∂
∂
v
z
v
y
v
x
,
,
×
∂
∂
∂
∂
∂
∂
=
→
u
z
u
y
u
x
,
,
N
∂
∂
∂
∂
∂
∂
v
z
v
y
v
x
,
,
v
u
Ω
d
d
d
⋅
=
P
RZYKŁAD
1. Płat w
postaci parametrycznej:
x
x
=
,
y
y
=
,
)
,
(
y
x
z
z
=
ma wektor prostopadły:
=
∂
∂
×
∂
∂
=
∂
∂
∂
∂
∂
∂
×
∂
∂
∂
∂
∂
∂
=
→
y
z
x
z
y
z
y
y
y
x
x
z
x
y
x
x
,
1
,
0
,
0
,
1
,
,
,
,
N
∂
∂
−
∂
∂
−
1
,
,
y
z
x
z
(
por. wzór 6 w tabeli
).
Opracował i wykonał: Stanisław Zoń
3
P
RZYKŁAD
2. Sfera
2
2
2
2
a
z
y
x
=
+
+
w
postaci parametrycznej.
)
cos(
)
sin(
ϕ
ϑ
a
x
=
,
)
sin(
)
sin(
ϕ
ϑ
a
y
=
,
)
cos(
ϑ
a
z
=
, obszar
{
}
π
ϑ
π
ϕ
Ω
≤
≤
≤
≤
=
0
,
2
0
:
ma wektor prostopadły:
=
∂
∂
∂
∂
∂
∂
×
∂
∂
∂
∂
∂
∂
=
→
ϕ
ϕ
ϕ
ϑ
ϑ
ϑ
z
y
x
z
y
x
,
,
,
,
N
[
] [
]
=
−
×
−
=
0
),
cos(
)
sin(
),
sin(
)
sin(
)
sin(
),
sin(
)
cos(
),
cos(
)
cos(
ϕ
ϑ
ϕ
ϑ
ϑ
ϕ
ϑ
ϕ
ϑ
a
a
a
a
a
[
]
)
cos(
),
sin(
)
(
sin
),
cos(
)
(
sin
)
sin(
2
ϑ
ϕ
ϑ
ϕ
ϑ
ϑ
a
=
→
N
,
)
sin(
|
|
2
ϑ
a
N
=
=
→
N
.
Wektor ten skierowany jest na zewnątrz sfery.
Ω
=
d
d
N
S
ϕ
ϑ
ϑ
ϕ
ϑ
d
d
)
sin(
d
d
2
⋅
=
⋅
=
a
N
,
∫∫
S
d
)
,
,
(
S
z
y
x
f
∫∫
⋅
=
Ω
ϕ
ϑ
ϑ
d
d
)
sin(
)
,
,
(
2
a
z
y
x
f
,
gdzie za x, y, z należy wstawić równania sfery. Całka po prawej stronie to zwykła całka podwójna.
P
RZYKŁAD
3. Walec
2
2
2
a
y
x
=
+
w
postaci parametrycznej,
)
cos(
ϕ
a
x
=
,
)
sin(
ϕ
a
y
=
,
z
z
=
, obszar
{
}
2
1
,
2
0
z
z
z
≤
≤
≤
≤
=
π
ϕ
Ω
:
ma wektor prostopadły:
[
] [
]
=
×
−
=
∂
∂
∂
∂
∂
∂
×
∂
∂
∂
∂
∂
∂
=
→
1
,
0
,
0
0
),
cos(
),
sin(
,
,
,
,
ϕ
ϕ
ϕ
ϕ
ϕ
a
a
z
z
z
y
z
x
z
y
x
N
[
]
0
),
sin(
),
cos(
ϕ
ϕ
a
=
→
N
,
a
N
=
=
→
|
| N
. Wektor ten skierowany jest na zewnątrz walca.
Ω
=
d
d
N
S
z
a
z
N
d
d
d
d
⋅
⋅
=
⋅
⋅
=
ϕ
ϕ
,
∫∫
S
d
)
,
,
(
S
z
y
x
f
∫∫
⋅
=
Ω
ϕ
dz
d
)
,
,
(
a
z
y
x
f
,
gdzie za x, y, z należy wstawić równania walca. Całka po prawej stronie to zwykła całka podwójna.
Operatory różniczkowe
we współrzędnych kartezjańskich (x,y,z)
Operacje różniczkowe najłatwiej zapisuje się przy pomocy operatora różniczkowego
nabla
:
x
x
x
z
y
x
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
∂
∂
∂
∂
=
∇
→
→
→
→
k
j
i
,
,
.
Gradient funkcji skalarnej:
∂
∂
∂
∂
∂
∂
=
∇
=
→
z
u
y
u
x
u
u
u
,
,
grad
,
Dywergencja pola wektorowego:
[
]
z
Z
y
Y
x
X
Z
Y
X
z
y
x
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
∂
∂
∂
∂
=
∇
=
→
→
→
,
,
,
,
div
o
o F
F
,
Laplasjan funkcji skalarnej:
2
2
2
2
2
2
lapl
z
u
y
u
x
u
u
u
∂
∂
+
∂
∂
+
∂
∂
=
∇
∇
=
→
→
o
,
Rotacja pola wektorowego:
[
]
Z
Y
X
z
y
x
,
,
,
,
rot
×
∂
∂
∂
∂
∂
∂
=
×
∇
=
→
→
→
F
F
,
∂
∂
−
∂
∂
∂
∂
−
∂
∂
∂
∂
−
∂
∂
=
∂
∂
∂
∂
∂
∂
=
y
X
x
Y
x
Z
z
X
z
Y
y
Z
Z
Y
X
z
y
x
,
,
k
j
i
r
r
r
.
Potencjałem pola wektorowego
)]
(
),
(
),
(
[
)
(
P
Z
P
Y
P
X
P
=
→
F
, gdzie punkt P ma współrzędne
)
,
,
(
z
y
x
,
nazywamy funkcję skalarną
)
,
,
(
)
(
z
y
x
u
P
u
=
taką, że
→
=
F
u
grad
czyli
Z
z
u
Y
y
u
X
x
u
=
∂
∂
=
∂
∂
=
∂
∂
,
,
.

Opracował i wykonał: Stanisław Zoń
4
Pole wektorowe
]
,
,
[
Z
Y
X
=
→
F
jest potencjalne w obszarze jednospójnym wt. i t. wt. gdy
→
→
=
0
F
rot
.
Rotacja
płaskiego pola wektorowego
]
0
),
,
(
),
,
(
[
y
x
Y
y
x
X
=
→
F
jest wektorem prostopadłym
do płaszczyzny Oxy o współrzędnych
→
F
rot
∂
∂
−
∂
∂
=
y
X
x
Y
,
0
,
0
.
Tw.
Greena. Jeżeli l jest krzywą zamkniętą zwykłą gładką lub kawałkami gładką
skierowaną dodatnio względem swego wnętrza, a pole wektorowe
]
0
),
,
(
),
,
(
[
y
x
Y
y
x
X
=
→
F
jest klasy C
1
w obszarze (G), to:
∫∫
∫
∂
∂
−
∂
∂
=
→
→
)
(
)
(
d
d
d
G
l
y
x
y
X
x
Y
l
F o
.
Tw.
Guassa. Jeżeli S jest powierzchiną regularną zamkniętą zorientowaną na
zewnątrz, a pole wektorowe
]
,
,
[
Z
Y
X
=
→
F
jest klasy C
1
w obszarze (V) za-
wartym wewnątrz S, to:|
∫∫∫
∫∫
→
→
→
=
)
(
)
(
d
d
V
S
V
div
F
S
F o
.
Wyszukiwarka
Podobne podstrony:
4.Całka różniczki zupełnej, MATEMATYKA, CAŁKI, CAŁKI KRZYWOLINIOWE I POWIERZCHNIOWE, 01Całki krzywol
Całki krzywoliniowe i powierzchniowe, Mechatronika WAT, Matma, Inne notatki zadania itp
2.Całka krzywoliniowa nieskierowana, MATEMATYKA, CAŁKI, CAŁKI KRZYWOLINIOWE I POWIERZCHNIOWE, 01Całk
3.Całka powierzchniowa zorientowana, MATEMATYKA, CAŁKI, CAŁKI KRZYWOLINIOWE I POWIERZCHNIOWE, 02Całk
LISTA 14 Całki krzywoliniowe
calki krzywoliniowe I i II rodzaju
03 2 Zastosowanie całki krzywoliniowej w mechanice
Całki krzywoliniowe
Sem 2. Wykład, Całki Krzywoliniowe
ANALIZA MATEMATYCZNA CAŁKI KRZYWO LINIOWE
Całki krzywoliniowe
Zadania.Calki krzywoliniowe, Oceanotechnika. PG, Semestr 2
LISTA 14, Całki krzywoliniowe
Całki krzywoliniowe, Matematyka
Arkusz nr 6 (Funkcja uwikłana i całki krzywoliniowe)
Arkusz nr 7 (całki potrójne i powierzchniowe)
Całki krzywoliniowe
więcej podobnych podstron