Zadania do tematu 3

1,2,6,8,9,11, 12/150;13,14/151

1/150

V = 100 cm³ roztworu amoniaku (NH₄OH) o stężeniu c_b = 0,10 mol/dm³

m_NaOH = 2,0 g

M_NAOH = 40,01 g/mol

I = 1A, pK_b = 4,33, K_b = 4,68∙10^-5; pcNH₄ = ?

Objętość roztworu nie zmienia się po dodaniu stałego NaOH, zatem V = 100 cm³ = 0,100 dm³

n_NaOH = m_NaOH/ M_NAOH = 2,0/40,01 = 0,0500 mol

c_NaOH = n_NaOH/V = 0,0500/0,100 = 0,500 mol/dm³

NH₄OH ↔ NH₄⁺ + OH^-

NaOH → Na⁺ + OH^-

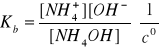
[NH₄⁺] = [OH^-]_NH4OH

[OH^-] = c_NaOH + [OH^-]_NH4OH = c_NaOH + [NH₄⁺]

[NH₄OH] = c_b - [[OH^-]_NH4OH = c_b - [NH₄⁺]

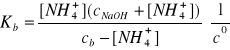
Założenie:

c_NaOH >> [NH₄⁺]

c_b >> [NH₄⁺]

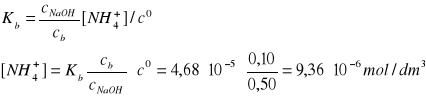
Z dokładnością do dwóch cyfr znaczących [NH₄⁺] = 9,4∙10^-6 mol/dm³. Ponieważ obydwa założenia są świetnie spełnione, zatem:

pcNH₄ = 5,03

2/150

Kwas octowy (HA), V₁ = 200 cm³, c_HA = 1,00 mol/dm³

+ V₂ = 1,0 cm³ kwasu solnego, c_HCl = 0,60 mol/dm³

I = 1A, pK_a = 4,55, K_a = 2,82∙10^-5

Obliczyć ΔpcH = pcH₁ - pcH₂

pcH₁ dotyczy sytuacji przed dodaniem HCl, tzn. wtedy gdy kwas octowy występuje w roztworze sam:

HA ↔ H⁺ + A^-

Ponieważ

[H⁺] = [A^-]

[HA] = c_HA - [H⁺]₁, to

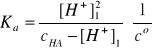
Założenie c_HA >> [H⁺]₁ jest spełnione, ponieważ
= 188,3.

Stąd [H⁺]₁ = 5,31∙10^-3 mol/dm³ oraz pcH₁ = 2,27

pcH₂ odnosi się do mieszaniny kwasów o objętości V = V₁ + V₂ = 201 cm³. Stężenia obydwu kwasów w tej mieszaninie są następujące:

HA ↔ H⁺ + A^-

HCl → H⁺ + Cl^-

[H⁺]_HA = [A^-]

[H⁺]₂ = c^'_HCl + [H⁺]_HA

[HA] = c^'_HA - [H⁺]_HA

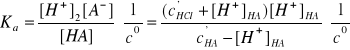
Obecnie można przyjąć tylko jedno założenie, mianowicie c^'_HA >> [H⁺]_HA, co prowadzi do równania kwadratowego zupełnego:

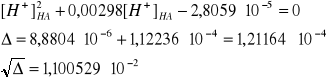
[H⁺]_HA = 4,01∙10^-3 mol/dm³

[H⁺]₂ = c^'_HCl + [H⁺]_HA = 2,98∙10^-3 + 4,01∙10^-3 = 7,0∙10^-3 mol/dm³

pcH₂ = 2,15

ΔpcH = pcH₁ - pcH₂ = 0,12 (z dokładnością do dwóch cyfr znaczących)

6/150

Kwas cyjanowodorowy HCN, dalej HA, V₁ = 500 cm³, c_HA = 0,0090 mol/dm³

+ V₂ = 1,00 cm kwasu solnego, c_HCl = 0,50 mol/dm³.

I = 2A, pK_a = 8,52, pK₂ = 3,02∙10^-9.

Obliczyć ile razy zmieni się stopień dysocjacji HCN, tzn. obliczyć stosunek α₁/α₂.

α₁ jest stopniem dysocjacji HCN przed dodaniem kwasu solnego:

HA ↔ H⁺ + A^-

Ponieważ

[H⁺]₁ = [A^-]

[HA] = c_HA - [H⁺]₁, to

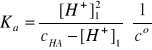
Założenie c_HA >> [H⁺] jest spełnione, ponieważ
= 1727. Stąd

[H⁺]₁ = 5,2∙10^-6 mol/dm³

α₁ = [H⁺]₁/c_HA = 5,8∙10^-4

α₁ = 0,058%

α₂ jest stopniem dysocjacji HCN w obecności kwasu solnego. Objętość mieszaniny kwasów:

V = V₁ + V₂ = 501 cm³

Stężenia obydwu kwasów w tej mieszaninie są następujące:

HA ↔ H⁺ + A^-

HCl → H⁺ + Cl^-

[H⁺]_HA = [A^-]

[H⁺]₂ = c^'_HCl + [H⁺]_HA

[HA] = c^'_HA - [H⁺]_HA

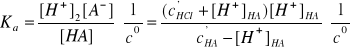
Założenia:

c^'_HA >> [H⁺]_HA

c^'_HCl >> [H⁺]_HA

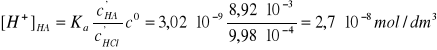
Założenia są bardzo dobrze spełnione. Zatem

α₂ = H⁺]_HA/ H⁺]_HA = 3,0∙10^-6

α₂ = 0,00030%

α₁/α₂ = 193. Końcowy wynik należy jednak podać z dokładnością do dwóch cyfr znaczących, wobec tego:

α₁/α₂ = 1,9∙10².

9/150

V = 1,00 dm³ roztworu amoniaku (NH₄OH), c_NH4OH = 0,025 mol/dm³. Obliczyć masę stałego KOH, aby po dodaniu do roztworu (objętość V pozostaje stała) stężenie jonów NH₄⁺ zmalało 10x.

I = 1A, pK_b = 4,33, K_b = 4,68∙10^-5

M_KOH = 56,11g/mol

m_KOH = ?

[NH₄⁺]₂ = [NH₄⁺]₁/10

Przed dodaniem KOH:

NH₄OH ↔ NH₄⁺ + OH^-

[NH₄⁺]₁ = [OH^-]

[NH₄OH] = c_NH4OH - [NH₄⁺]

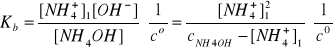
Do obliczenia stężenia jonów amonowych nie stosujemy wzoru uproszczonego, ponieważ:

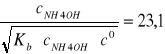
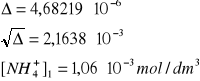
Po dodaniu KOH:

NH₄OH ↔ NH₄⁺ + OH^-

KOH → K⁺ + OH^-

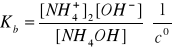
[NH₄⁺]₂ = [NH₄⁺]₁/10 = 1,06∙10^-4 mol/dm³

[OH^-] = c_KOH + [NH₄⁺]₂

[NH₄OH] = c_NH4OH - [NH₄⁺]₂

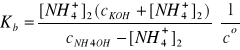
Po przekształceniu otrzymujemy:

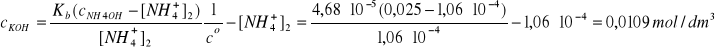
n_KOH = V∙c_KOH

m_KOH = V∙c_KOH∙M_KOH = 0,0109∙56,11 = 0,61g KOH (dwie cyfry znaczące)

11/150

Mocny kwas HX, c₁ = 2,5∙10^-3 mol/dm³, pcH₁ = ?

R = 5000, c₂ = c₁/R = 2,5∙10^-3/5000 = 5,0∙10^-7 mol/dm³, pcH₂ = ?

ΔpcH = pcH₂ - pcH₂

I = 1A, pK_w = 13,80; K_w = 1,58∙10^-14

Przed rozcieńczeniem

HX → H⁺ + X^-

[H⁺]₁ = c₁ = 2,5∙10^-3 mol/dm³

pcH₁ = 3 - log 2,5 = 2,60

Po rozcieńczeniu

Stężenie HX, c₂ = 5,0∙10^-7 mol/dm³ jest w obszarze stężenia granicznego, dlatego:

HX → H⁺ + X^-

H₂O ↔ H⁺ + OH^-

[H⁺] = c₂ + [H⁺]_w

[H⁺]_w = [OH^-]

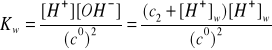
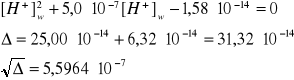
[H⁺]_w = 2,98∙10^-8 mol/dm³

[H⁺]₂ = c₂ + [H⁺]_w = 5,0∙10^-7 + 2,98∙10^-8 = 5,3∙10^-7

pcH₂ = 7 - log 5,3 = 6,28

ΔpcH = pcH₂ - pcH₂ = 3.68 (odpowiedź podana w skrypcie 3,67).

12/150

V₁ = 20,0 cm³ r-ru KOH, c₁ = 0,020 mol/dm³ dodano do V₂ = 1,50 m³ = 1,50∙10⁶ cm³ roztworu NaClO₄. UWAGA: NaClO₄ reguluje siłę jonową (I = 1A) uzyskanego roztworu KOH o stężeniu c₂ = 2,67∙10^-7 mol/dm³, które jest w obszarze stężeń granicznych.

pK_w = 13,80, pK_w =1,58∙10^-14. Obliczyć zmianę ΔpcH = pcH₁ - pcH₂.

Przed rozcieńczeniem

KOH → K⁺ + OH^-

[OH^-]₁ = c₁ = 0,020 mol/dm³

pcOH₁ = 2 - log 2 = 1,70

pcH₁ = pK_w - pcOH₁ = 13,80 - 1,70 = 12,10

Po rozcieńczeniu

KOH → K⁺ + OH^-

H₂O ↔ H⁺ + OH^-

[OH^-]₂ = c₂ + [OH^-]_w

[H⁺] = [OH^-]_w

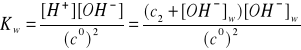
Δ = 7,1289∙10^-14 + 6,3200∙10^-14 = 13,4489∙10^-14

[OH^-]_w = 4,99∙10^-8 mol/dm³

[OH^-]₂ = 2,67∙10^-7 + 4,99∙10^-8 = 3,2∙10^-7 mol/dm³

pcOH₂ = 7 - log 3,2 = 6,50

pcH₂ = pK_w - pcOH₂ = 13,80 - 6,50 = 7,30

ΔpcH = pcH₁ - pcH₂ = 4,80

---