INTERWAŁ W PRZESTRZENIACH O RÓŻNEJ KRZYWIŹNIE.
Jednym z podstawowych problemów kosmologii jest rozstrzygnięcie globalnej krzywizny przestrzeni Wszechświata. Z doświadczenia wiemy, że lokalnie przestrzeń naszą możemy opisywać geometrią euklidesową. Globalne własności natomiast opisują odpowiednie równania OTW (przedstawiane w rozdziale - kosmologiczne równania Friedmana). We wstępie do OTW (patrz rozdział: podstawy OTW) mówi się, że podstawowym obiektem matematycznym charakteryzującym własności geometryczne czasoprzestrzeni jest tzw. interwał czasoprzestrzenny, który w płaskiej czasoprzestrzeni ma postać:
ds2 = (dx0)2 - (dx1)2 - (dx2)2 - (dx3)2 (1)
Ze względu na izotropowość przestrzeni wygodnie jest przejść od współrzędnych kartezjańskich
(x1, x2, x3) współrzędnych sferycznych:
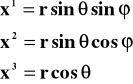
(2)
Wówczas przestrzenna część interwału (1) (po prostych różniczkowaniach) przybierze postać:
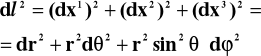
(3)
Od czasów odkrycia Hubble'a (1929) wiemy, ze przestrzeń Wszechświata ekspanduje. Wszystkie punkty wzajemnie oddalają się nie zmieniając jednak swoich współrzędnych (względem przyjętej siatki współrzędnych ). To trochę tak jakby nadmuchiwać Ziemie (jak balon), wówczas wszystkie miejscowości oddalają się od siebie nie zmieniając jednak swoich współrzędnych geograficznych. Aby ten fakt uwzględnić wygodnie jest wprowadzić tzw. „czynnik skalujący” - R(t) - który mówi nam przez jaką wielkość trzeba przemnożyć odległość pomiędzy dwoma punktami przestrzeni po upływie czasu t . A więc formułę (3) zapiszemy w postaci:
![]()
(3a)
Formuły (1) - (3a) dotyczyły przestrzeni euklidesowej. Teraz zapiszemy interwał (3a) w ogólniejszej formie uwzględniającej możliwą globalną krzywiznę przestrzeni. Przestrzeń nasza nie musi być bowiem globalnie euklidesowa. Może ona mieć własności geometryczne podobne do powierzchni sferycznej (np. suma kątów trójkąta jest wtedy większa od 180o ) lub też własności podobne do powierzchni hiperboloidalnej (gdzie suma kątów trójkąta jest mniejsza od 180o). Prześledzimy to na przykładzie sfer o geometrii sferycznej.
jednowymiarowa sfera (okrąg) o promieniu `r' na płaszczyźnie euklidesowej.
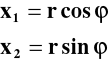
![]()
Interwał długości: ![]()
(4)
Kąt oraz promień krzywizny r leżą poza linią okręgu (nie należą do tej jednowymiarowej przestrzeni). Długość okręgu („objętość” tej jednowymiarowej przestrzeni ) jest skończona i wynosi 2r.
(II) dwuwymiarowa powierzchnia sfery o promieniu `a' w 3-wymiarowej przestrzeni euklidesowej
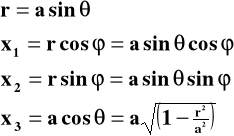
Interwał długości (po prostych różniczkowaniach) otrzymamy:
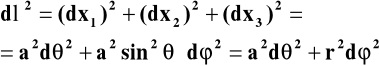
(5)
Promień krzywizny sfery `a' oraz kąt leżą poza powierzchnią sfery (nie należą do tej dwuwymiarowej przestrzeni). Powierzchnia sfery („objętość” tej dwuwymiarowej przestrzeni) jest skończona i wynosi 4a2.
Obwód dowolnego okręgu o promieniu `r' na sferze:
![]()
Natomiast pole powierzchni takiego koła
![]()
jest mniejsze niż przykrywające go pole czaszy kulistej.
III 3-wymiarowa hipersfera o promieniu R w 4-wymiarowej przestrzeni euklidesowej
Przez analogię z punktem (II) napiszemy równanie hipersfery
![]()
(tu x4 to zwykła czwarta współrzędna przestrzenna - nie mylić jej ze współrzędną czasową)
![]()
I dalej przez analogię podstawimy ![]()
.
Promień hipersfery R oraz współrzędna kątowa nie leżą w przestrzeni naszej hipersfery (tak jak promień krzywizny a oraz kąt leżały poza powierzchnią sfery w przykładzie II).
Współrzędne hiper(sferyczne) będą teraz:
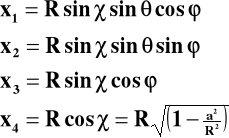
Interwał przestrzenny będzie teraz:
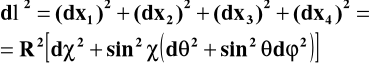
(6a)
Ponieważ ![]()
więc
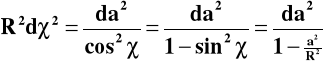
a stąd interwał przestrzenny
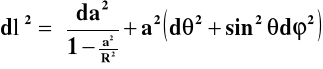
(6b)
Składowe tensora metrycznego będą tu następujące:
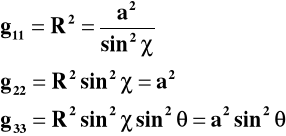
Nasza hipersferyczna przestrzeń ma też skończoną objętość
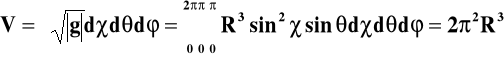
Możemy także stosunkowo łatwo opisać przestrzeń o ujemnej krzywiźnie - tzw. hiperboliczną - przez prostą zamianę funkcji sin na jej odpowiednik hiperboliczny sinh oraz korzystać z jedynki trygonometrycznej dla funkcji hiperbolicznych cosh2 - sinh2 = 1 Wówczas interwał przestrzenny dla takiej 3-wymiarowej przestrzeni z ujemną krzywizną będzie:
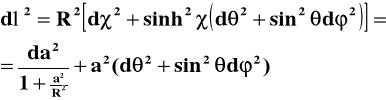
(7)
![]()
Gdy krzywizna ![]()
, co oznacza przechodzenie do przestrzeni „płaskiej”, to interwał
![]()
(8)=(3)
czyli otrzymujemy cos identycznego jak w formule (3).
Wprowadzimy sobie teraz bezwymiarową współrzędną radialną 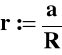
lub da = R dr,
(nie należy mylić i utożsamiać jej z promieniem okręgu `r' z przykładu (I), to całkiem nowe oznaczenie!!!).
Wprowadźmy też sobie następującą wielkość, k, przyjmującą trzy możliwe wartości:
k = 0 dla przestrzeni euklidesowej,
k = +1 dla geometrii typu sferycz ):nego,
k = -1 dla geometrii typu hiperbolicznego.
Wówczas interwał przestrzenny uwzględniający wszystkie trzy możliwości - czyli formuły (6a,b), (7) i (8) da się zapisać jedną formułą (uwzględniającą już możliwość ekspansji przestrzeni :czyli zależność R=R(t) ):
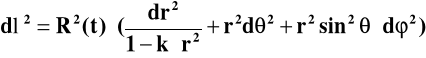
(9)
Współrzędna r jest tu wielkością bezwymiarową zaś R ma wymiar długości. W niektórych ujęciach monograficznych bywa stosowane podejście, w którym kosmologiczny czynnik skali odległości R(t) traktuje się jako bezwymiarowy natomiast wymiar długości przenoszony jest do współrzędnej r.
My w kolejnych rozdziałach będziemy jednak traktować czynnik R(t) jako posiadający wymiar długości.
Rozpatrzmy jeszcze dla prostoty odległość dl tylko wzdłuż współrzędnej radialnej `r'.
Wówczas dla k = +1 mamy:
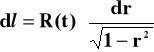
(10)
co po scałkowaniu stronami daje nam :
![]()
lub : 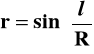
(11)
Dla małych wartości l lub dużych R stosowne jest przybliżenie ![]()
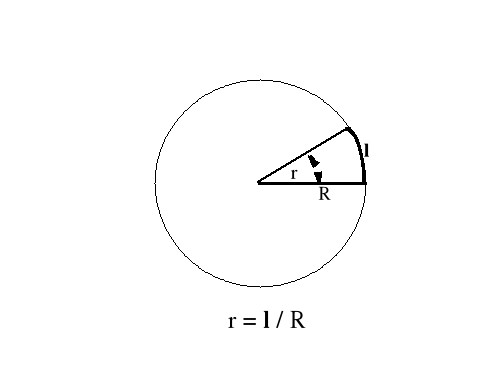
Można tu dostrzec podobieństwo do zależności między długością łuku a promieniem na powierzchni kuli (patrz poniższy rysunek)
W przypadku k = +1 mamy więc przestrzeń o własnościach hipersfery zaś czynnik skali R(t) jest jakby (zmiennym w czasie) promieniem tej hipersfery. Przestrzeń taka ma skończoną objętość (tak jak powierzchnia sfery ma skończone pole) równą V = 22R3 .
Dla k = -1 formuła (10) będzie:
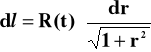
(12)
co po scałkowaniu da nam funkcję hiperboliczną: ![]()
W tym sensie przestrzeń taka jest jakby trójwymiarową hiperboloidą o ujemnej krzywiźnie. Przestrzeń taka ma nieskończoną objętość.
Interwał czasoprzestrzenny dla potrzeb kosmologii zapisuje się więc
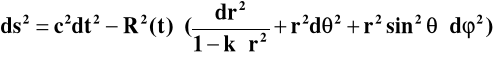
(13a)
lub z użyciem współrzędnej kątowej :
![]()
(13b)
gdzie:
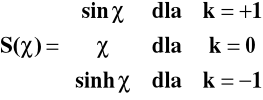
![]()
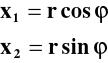
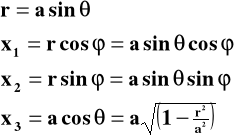
![]()
![]()
Wyszukiwarka
Podobne podstrony:
LAMBDA, Kompendium wiedzy z fizyki
tabela wzor, Kompendium wiedzy z fizyki
ANTROPIC, Kompendium wiedzy z fizyki
ERA PROM, Kompendium wiedzy z fizyki
DISTANCE, Kompendium wiedzy z fizyki
WHEELER, Kompendium wiedzy z fizyki
HORYZONT, Kompendium wiedzy z fizyki
ERA LEP, Kompendium wiedzy z fizyki
KOSMOLOG, Kompendium wiedzy z fizyki
HUBBLE, Kompendium wiedzy z fizyki
Teoria względności, Kompendium wiedzy z fizyki
PRZYMIOTNIKI, Gramatyka - kompendium wiedzy (kala101)
małe kompendium wiedzy o wulkanach, Geografia, Geologia dynamiczna
CZĘŚCI MOWY, Gramatyka - kompendium wiedzy (kala101)
Stopniowanie przymotnika, Gramatyka - kompendium wiedzy (kala101)
!!! KOMPENDIUM WIEDZY !!, 24-25, 23.6 Warto˙ci skuteczne pr˙du elektrycznego zmiennego.
Czy płacenie kartą w Internecie jest bezpieczne Kompendium wiedzy dla Ciebie - część III, Porady róż
więcej podobnych podstron