PROBLEM STAŁEJ KOSMOLOGICZNEJ,

fatalna czy genialna pomyłka Einsteina?

Jedną z pierwszych prób zastosowania równań OTW do modelowania Wszechświata było podejście samego Einsteina (1917 rok). Znał on dobrze tzw. paradoksy, do których prowadziła w tym zakresie teoria newtonowska (paradoks Olbersa, paradoks grawitacyjny). Według ówczesnego stanu wiedzy (było to przed odkryciem Hubble'a) jedynym sensownym rozwiązaniem wydawał się Einsteinowi statyczny model Wszechświata o geometrii typu sferycznego. W modelu takim Wszechświat miałby skończoną objętość lecz bez „brzegów”. Jednak z einsteinowskich równań pola w ich pierwotnej postaci nie sposób było otrzymać takiego statycznego modelu - model taki bowiem „zapadał” się pod wpływem grawitacyjnego oddziaływania zawartej w nim materii. Wobec tego Einstein zmodyfikował swoje równania OTW dodając do nich arbitralnie dodatkowy człon skalarny -  - nazwany stałą kosmologiczną. Równania jego wyglądały więc po tej modyfikacji (patrz też rozdział: Podstawy OTW):

(1)

Człon  , podobnie jak skalar krzywizny przestrzeni, ma wymiar [m^-2].

Prezentowane w rozdziale - kosmologiczne rozwiązania równań Einsteina - równania (3) i (4) mają teraz, po uwzględnieniu stałej kosmologicznej, postać:

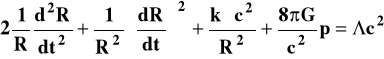
(2)

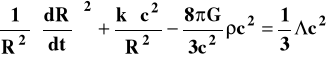
(3)

Ponieważ model miał być statyczny - R = const - czyli pochodne R po czasie zerują się, więc z równań (2) i (3) otrzymamy:

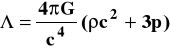
(4)

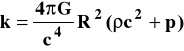
(5)

Widać, że tylko przypadek k = +1 (geometrii sferycznej) wchodzi tu w grę, gdyż dla k = 0 lub k = -1 dostajemy zerowe lub ujemne gęstości i/lub ciśnienia (co byłoby fizycznie bez sensu). Również z tego samego powodu musi być >.

Z obserwacji wiadomo, że średnia gęstość materii barionowej we Wszechświecie jest nie większa niż ρ  5*10^-31 g/cm³ (lub N = 1 atom na m³).

Gdyby więc całą materię gwiazd i galaktyk równomiernie rozproszyć to jej temperatura byłaby rzędu 3 [K] a jej ciśnienie p << ρc² jest zaniedbywalnie małe.

Odejmując stronami równanie (3) od (2) dostaniemy:

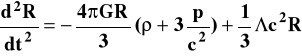
(6)

Jeśli lewa strona ma się zerować (bo R = const) to znaczy, że wyraz c²R/3 ma fizyczny sens przyspieszenia równego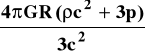
lecz skierowanego przeciwnie - taki rodzaj siły odpychającej i zapobiegającej grawitacyjnemu zapadnięciu się materii Wszechświata.

Po odkryciu przez Hubble'a w 1929 roku faktu ekspansji Wszechświata Einstein porzucił koncepcję modelu statycznego a wprowadzenie do swoich równań stałej kosmologicznej nazwał swoją największą pomyłką. Jednak równania Einsteina (2) i (3) ze stałą  oraz R = R(t) nie tracą nic na swej ogólności matematycznej, wzbogacają natomiast rodzinę możliwych rozwiązań kosmologicznych. I tak np. tzw. gęstość krytyczna materii, przy której ekspandujący Wszechświat Friedmanna posiada geometrię euklidesową (k = 0 ) ma przy uwzględnieniu członu  postać:

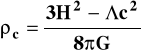
(7)

(gdzie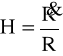
jest parametrem Hubble'a). Szczególnym przypadkiem jest też tzw. „pusty” Wszechświat de Sittera, w którym p = ρ = 0, k = 0 lecz >.

Wówczas z równania (3) dostajemy rozwiązanie:

(8)

czyli exponencjalne tempo rozszerzania się. W tym przypadku parametr Hubble'a

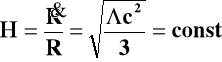
(9)

jest stały. Model taki nie ma też osobliwości w chwili t=0, tu
gdy
.

Ze stałej kosmologicznej można też zbudować wielkość o wymiarze ciśnienia - nazwano je „ciśnieniem fizycznej próżni” - p_vacuum :

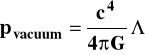
(10)

Wówczas równanie (6) będzie:

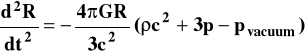
(11)

Pojawiają się ostatnio obserwacyjne wskazówki sugerujące, że jakaś forma tego ujemnego ciśnienia próżni istnieje i powoduje przyspieszającą nieco ekspansję.

Zauważmy, że równanie (3) dla k=0 można zapisać:

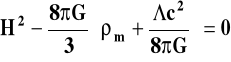
(12a)

lub

(12b)

i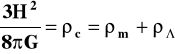
(12c)

gdzie: ρ_m - gęstość materii zaś ρ_ to jakby gęstość odpowiadająca energii próżni.

Parametr charakteryzujący gęstość,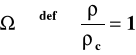
dla modelu z k=0, można więc go zapisać jako

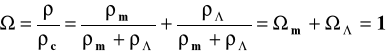
(13)

Parametr Hubble'a dla modelu „płaskiego” (k=0) bez stałej kosmologicznej () wyrażał się
, a stąd obecny wiek Wszechświata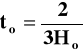
. Z obserwacji otrzymuje się obecną wartość H_o = 65 km/s/Mpc co daje wiek Wszechświata ok. 10 mld. lat. Jest to niepokojąco mała wartość albowiem znane są w kosmosie obiekty (niektóre stare gwiazdy), których wiek (określany na podstawie naszej wiedzy o ewolucji gwiazd) szacowany jest na nieco ponad 10 mld. lat. Pojawił się więc kłopotliwy „problem wieku Wszechświata”. Uwzględnienie w modelach kosmologicznych stałej  pozwala na odsunięcie tego kłopotliwego problemu. Wiek Wszechświata otrzymywany z równań kosmologicznych (3) i (12) gdy k=0 i > wyraża się bowiem formułą:

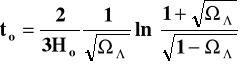
(14)

(można sprawdzić, że granica: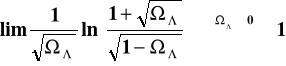

a tym samym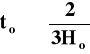
gdy
).

Jeśli przykładowo założymy sobie wartości _   oraz _m = 0.25 to z formuły (14) otrzymamy wiek Wszechświata

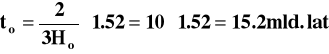
a więc wartość korzystniejszą. Widzimy więc w jakim kierunku działa czynnik . Czynnik ten ma jeszcze jeden znaczący wpływ na sposób ekspansji kosmologicznej. Otóż, jak wiadomo, gęstość materii maleje w miarę ekspansji. W modelu „płaskim” z  mieliśmy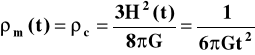
. Natomiast gęstość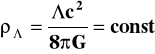
. A więc, jeśli nawet na wczesnym etapie ewolucji Wszechświata dominowała gęstość materii (ρ_m>>ρ_) i ekspansja odbywała się tak jak to wynika z równań Friedmanna bez stałej kosmologicznej (ekspansja spowalniająca) to w miarę upływu czasu wpływ czynnika  staje się coraz bardziej znaczący i od pewnego momentu wręcz dominujący (gdy ρ_m<<ρ_ ). Sposób ekspansji zbliża się bowiem wówczas do postaci opisywanej rozwiązaniem de Sittera (8) - ekspansji eksponencjalnej, silnie przyspieszającej.

Od połowy lat 90-tych realizowany jest program obserwacyjny mający na celu rozstrzygnięcie, czy faktycznie tempo ekspansji Wszechświata wykazuje pewien efekt przyspieszania. Poszukuje się wybuchów supernowych - zwłaszcza w dalekich galaktykach. Szczególnie użyteczne są tu tzw. supernowe typu SN_Ia, dla których mamy dość dobrze wykalibrowaną jasność absolutną M_v w maksimum blasku. Wynosi ona ok. -19^M.2 +/- 0.25 . Mając z obserwacji jasność widzialną tej supernowej, m_v , możemy ze znanego fotometrycznego wzoru:

policzyć odległość d (w parsekach) jaką przebyło światło od galaktyki z supernową do nas. Jednocześnie, mierząc `redshift'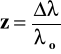
tej galaktyki, można policzyć tę odległość korzystając z prawa Hubble'a uwzględniając zmienność w czasie parametru Hubble'a H(t) w zależności od typu modelu kosmologicznego (ze stałą  lub bez niej ). Dane obserwacyjne wyraźnie sugerują, że najlepszą zgodność uzyskuje się dla modeli z k=0 i  = 0.75 +/- 0.1. Wskazują one, że Wszechświat wszedł już w fazę, w której ρ_>ρ_m a więc w fazę przyspieszającej ekspansji. Jest to bardzo interesujący rezultat wskazujący na znaczenie stałej kosmologicznej, chociaż nie bardzo jeszcze wiemy, co ona dzisiaj tak właściwie fizycznie oznacza. Wysuwane są różne hipotezy na ten temat.

Na początku lat 80-tych koncepcja stałej kosmologicznej uzyskała jakby nową interpretację fizyczną właśnie jako miernik tzw. ujemnego ciśnienia próżni fizycznej, które mogło odegrać podstawową rolę w bardzo wczesnej fazie ekspansji Wszechświata zwanej fazą inflacyjną. W tym krótkim niezmiernie ułamku sekundy rzędu 10^-35 s. mogła mieć miejsce exponencjalna ekspansja, podobnie jak w modelu de Sittera, która spowodowała to, ze geometria Wszechświata jest tak bliska euklidesowej a reliktowe promieniowanie tła tak dalece jednorodne. Być może to jakaś resztkowa część tego ujemnego ciśnienia próżni powoduje dziś przyśpieszającą ekspansję. Einstein zapewne byłby zdziwiony widząc obecny renesans swojej fatalnej - a może właśnie genialnej - pomyłki.

---