Uczelnia				Kierunek/rok studiów
Państwowa Wyższa Szkoła Zawodowa w Pile.				Transport (niestacjonarne) / I
Laboratorium - Fizyka
Wykonał:
Data wykonania ćwiczenia: 22.11.2012r.	Data oddania ćwiczenia: 01.12.2012r.		Temat: Wyznaczanie temperaturowego współczynnika oporu dla platyny za pomocą mostka Wheatstonea.		Ćwiczenie 7
										Ocena:	Sprawdził:

1. Wprowadzenie.

2. Zestaw pomiarowy.

3. Przebieg ćwiczenia

4. Zestawienie wyników pomiarowych, obliczenia.

5. Wnioski.

6. Załącznik.

1. Wprowadzenie
   

1. Mostkiem Wheatstone'a nazywamy pokazany na rysunku układ elementów elektrycznych służących do pomiaru oporu elektrycznego. Obwód mostka składa się z dwóch równolegle połączonych gałęzi ACB i ADB. Punkty A i B połączone
   są z źródłem prądu stałego(przez opornik R_z), a punkty C i D z galwanometrem lub czułym mikroamperomierzem. Oporniki R_p i R₂ mogą być dwiema częściami potencjometru dekadowego, wtedy punkt C odpowiada suwakowi potencjometru. Suma oporów R_p i R₂ jest wielkością stałą. Pomiar polega na takim dobraniu położenia punktu C, by przez galwanometr nie płynął prąd wtedy mówimy - mostek jest zrównoważony. Przy zrównoważonym mostku, pomiędzy punktami C
   i D nie ma różnicy potencjałów (U_CD = 0), a przez oporniki X₁ i R₁ płynie prąd
   o takim samym natężeniu I₁. Również przez oporniki R_p i R₂ płynie prąd o takim samym natężeniu I₂. Wtedy zgodnie z II prawem Kirchhoffa napisać możemy następujące związki:

;

Dzieląc pierwsze równanie przez drugie otrzymamy:

________________________________________________________________

2. Schemat mostka Wheatstone'a:

• Opór elektryczny zależy nie tylko od kształtu geometrycznego przewodnika
  i materiału, z którego jest wykonany ale również od temperatury.
  Dla metali opór elektryczny rośnie wraz ze wzrostem temperatury zgodnie
  z zależnością:

Gdzie:
α - oznacza temperaturę współczynnika oporu
ΔT - oznacza zmianę temperatury
R₀ - oznacza opór cząstkowy

2. Zestaw pomiarowy.

Doświadczenie przeprowadzamy wykorzystując następujące materiały
i przyrządy:

• Mostek Wcheatstone'a

• Źródło prądu stałego

• Termometr

• Płytka grzejna

• Czujnik platynowy

• Naczynie z wodą

• Przyrządy pomiarowe (omomierz)

3. Przebieg ćwiczenia

Sposób wykonania pomiarów zależy od typu zastosowanych przyrządów. Układ łączymy według schematu pokazanego na rysunku 1.2. Dla ułatwienia pomiaru wskazana jest znajomość przybliżonej wartości oporu opornika mierzonego , w tym celu mierzymy opór za pomocą omomierza.
Włączamy prąd i dobieramy tak położenie ruchomego styku by wychylenie galwanometru zredukować do zera. Po uzyskaniu zerowego wychylenia odczytujemy wskazanie wartości oporu X. Wyłączamy źródło prądu oraz kontrolujemy wskazanie zerowe galwanometru. Włączamy układ ponownie, ponownie kompensujemy układ otrzymując kolejną wartość oporu X. Liczbę pomiarów uzależniamy od sposobu obliczania błędu w tym przypadku
będzie to regresja liniowa , wykres zależności oporu od temperatury.

Dokonujemy kolejno pomiarów dla przedziału temperatur 23,9 - 100 °C.

Zaczynając od temperatury początkowej T₁=23,9°C mierzymy wartość oporu
co 5°C aż do momentu w którym wartość temperatury osiągnie T_k=100°C.
W ten sposób otrzymamy określoną ilość pomiarów oporu
dla konkretnej wartości temperatury, na podstawie których będziemy mogli wykreślić zależność oporu od temperatury - regresji liniowej.

4. Zestawienie wyników pomiarowych.

Pierwszego pomiaru oporu dokonałem zaczynając od temperatury wody T₁ = 23.9°C
Ostatniego pomiaru dokonałem natomiast w trakcie wrzenia wody T_k = 100°C.

4.1.Tabela wyników pomiarowych:

• Wartości oporu dla 16 pomiarów temperatury

• Wartość α dla 8 kolejnych par pomiarowych

Lp	T[°C]	R[Ω]	T2*R1-T1*R2	R2-R1[Ω]	α
1	23.9	110	526,10	1	0,0019
2	28.9	111
3	35.0	114				535,00	1	0,0018
4	40.0	115
5	45.0	117				495,00	2	0,0040
6	50.0	119
7	55.0	121				495,00	2	0,0040
8	60,0	123
9	65.0	125				495,00	2	0,0040
10	70,0	127
11	75.0	129				495,00	2	0,0040
12	80,0	131
13	85.0	133				495,00	2	0,0040
14	90.0	135
15	95,0	137				590,00	1	0,0016
16	100	138

Wartości oporu dla konkretnej temperatury zgodne z załącznikiem nr 1

4.2. Korzystając z następującego wzoru na zależność oporu od temperatury,
dla określonych par pomiarowych obliczamy wartość α




Po przekształceniu tego wzoru otrzymujemy:




___________________________________________________________________

4.3. Średnia wartość α:







___________________________________________________________________

1. Odchylenie standardowe :


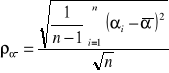
, przy czym





1. Wartość α z uwzględnieniem błędu pomiarowego:




___________________________________________________________________

5. Wnioski:

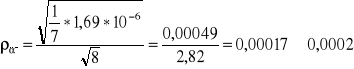
Na uzyskanie średniej wartości α oraz wartości oporu,
dla poszczególnych temperatur miały wpływ:

• Dokładność odczytu temperatury z termometru.

• Dokładność urządzeń pomiarowych (omomierz).

6. Załącznik:


1) Wartości pomiarów doświadczenia w laboratorium w dniu - 14.10.2012r.

---