Robert Maniura

Sprawozdanie z ćwiczenia nr 1: Siła elektromotoryczna ogniwa galwanicznego.

1. Wyniki ćwiczenia:

nr	Rodzaj ogniwa	SEM ogniwa [V]
1		1,046
2		0,051
3		1,098
4		1,111
5		1,079
6		1,095
7		0,012
8		-0,014
9		-0,020
10		-0,034
11		-0,044
12		-0,055

2. Wstęp teoretyczny:

Układ utworzony przez połączenie dwóch elektrod za pomocą przewodnika elektrolitycznego nosi nazwę ogniwa elektrochemicznego.

Zbudujmy ogniwo składające się z dwóch elektrod, przy czym na jednej z tych elektrod zachodzi wydzielanie kationów:

a na drugiej - przechodzenia jonów metalu do roztworu:

Sumaryczna reakcja w ogniwie w stanie równowagi będzie następująca:

Potencjały poszczególnych elektrod, zgodnie z równaniem Nernsta, wynoszą:

oraz

W przypadku roztworów rozcieńczonych aktywności jonów można zastąpić stężeniem molowym i po uproszczeniu równania te przybierają postać:

oraz

Siła elektromotoryczna
powstałego ogniwa będzie równa różnicy potencjałów elektrod:

a zatem:

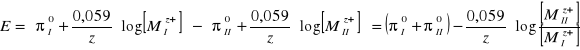
Różnica potencjałów standardowych elektrod
jest dla danego ogniwa stała. Nazwano ją standardową siłą elektromotoryczną ogniwa i oznaczono symbolem

1. Konwencja elektrochemiczna.

W 1953 r w Sztokholmie została przyjęta międzynarodowa konwencja ustaleń stosowanych w zapisie schematów ogniw elektrochemicznych i oznaczenia siły elektromotorycznej (SEM). Według tej konwencji SEM danego ogniwa jest dodatnia wtedy, gdy reakcja w ogniwie przebiega samorzutnie, oraz ujemna, gdy jest wymuszona.

Rozpatrzymy ogniwo Daniella, w którym zachodzą procesy:

Katoda:

Anoda:

Proces sumaryczny w stanie równowagi chemicznej:

Ogniwo Daniella składa się z dwóch naczyń zawierających roztwory ZnSO₄ i CuSO₄, z zanurzonymi w nich płytkami metalowymi: Zn i Cu. Roztwory te połączone są kluczem elektrolitycznym, który stanowi nasycony roztwór KCl. Jaką rolę w ogniwie spełnia właściwie klucz elektrolityczny?

Otóż, jeśli zetkną się ze sobą roztwory o różnym stężeniu, to na granicy styku tych roztworów wystąpi pewna różnica potencjałów, zwana potencjałem dyfuzyjnym. Potencjał ten wystąpi tylko wówczas, gdy liczby przenoszenia kationów i anionów stykających się elektrolitów będą różne.

Istnieją jednak pewne elektrolity, dla których liczby przenoszenia jonów są równe. Należą do nich np.: KCl, NH₄NO₃, KNO₃. dla roztworów tych substancji potencjał dyfuzyjny będzie prawie równy zeru.

Gdybyśmy bezpośrednio zetknęli ze sobą roztwory ZnSO₄ i CuSO₄, to w ogniwie wystąpiłby znaczny potencjał dyfuzyjny; umieszczenie między nimi klucza elektrolitycznego eliminuje ten potencjał. Konstrukcje kluczy mogą być rozmaite. Według konwencji sztokholmskiej schemat ogniwa Daniella zapisujemy jako:

gdzie
- oznacza klucz elektrolityczny.

Siłę elektromotoryczną SEM ogniwa można bezpośrednio za pomocą czułego miliwoltomierza bądź metodą kompensacyjną Poggendorffa. Schemat pomiarowy stosowany w metodzie Poggendorffa pokazano na poniższym rysunku.

Zasada pomiaru jest następująca: najpierw włącza się do obwodu ogniwo badane o nie znanej sile elektromotorycznej
i styk przesuwa się wzdłuż drutu oporowego do punktu
, aż galwanometr nie będzie wskazywał przepływu prądu. Do tego położenia spełniony jest warunek:
. Następnie podobny pomiar wykonuje się po zastąpieniu tego ogniwa ogniwem wzorcowym o znanej sile elektromotorycznej
. Wówczas kompensacja zajdzie przy innym położeniu styku na drucie oporowym, np. w punkcie
. Spełniona jest wtedy równość:
. Z tych zależności wynika, że

uwzględniając wzory:
i
otrzymamy ostatecznie:

Określenie siły elektromotorycznej ogniwa
wymaga zatem tylko pomiaru długości odcinków drutu oporowego w warunkach kompensacji w przypadku ogniwa badanego i wzorcowego.

3. Opracowanie wyników:

Wykorzystując wzór
oraz dane doświadczalne obliczam potencjały normalne elektrod
, obliczam błąd procentowy. Do obliczenia SEM ogniwa w tabeli poniżej wykorzystałem następujące daną:
.

nr	Rodzaj elektrody	Potencjał normalny (obliczony) [V]	Potencjał normalny (tablicowy) [V]	Błąd procentowy
1		-0,7668	-0,761	4,57 %
2		-0,7798	-0,7905	1,35 %
3		0,3312	0,339	2,30 %
4		0,3122	0,3095	8,50 %
5		0,2832	0,2800	1,14 %
6		0,2502	0,2505	0,12 %
7		0,2262	0,2210	2,35 %
8		0,1912	0,1915	0,16 %
9		0,1652	0,1620	1,97 %

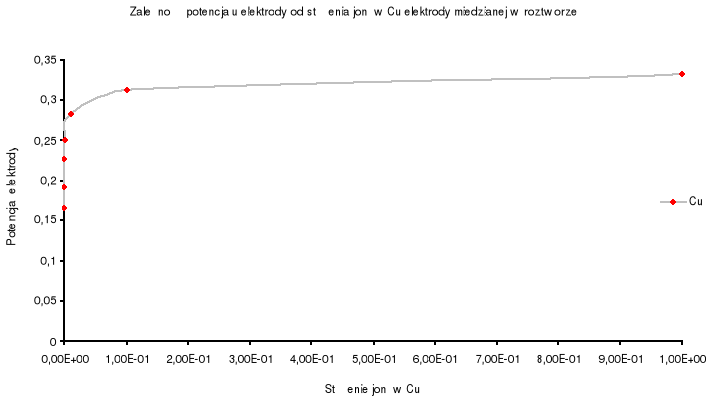
Wyznaczam zależność potencjału elektrody od stężenia jonów
elektrody w roztworze.

4. Wnioski:

Ponieważ źródła podają różne wartości potencjałów normalnych dla elektrod typu
, dlatego błędy dla
i
są znaczące. Nie zważając jednak na te błędy to w przypadku elektrod z rozcieńczeniami są raz znaczące, raz mniej znaczące. Wszystkie te błędy spowodowane są przede wszystkim niedokładnym dokonaniem rozcieńczeń jak również zbyt krótkim czasem oczekiwania na ustalenie się stanu równowagi w zmontowywanych ogniwach galwanicznych.

Z wykresu zależności potencjału elektrody od stężenia jonów
elektrody w roztworze wynika, że wraz ze wzrostem stężenia jonów metalu w roztworze potencjał elektrody wzrasta, co spowodowane jest zmniejszającą się aktywnością jonów w roztworze.

5. Literatura:

Kazimierz Gumiński „Wykłady z chemii fizycznej”;

Wiesław Karpiński „Chemia fizyczna dla techników chemicznych”

Peter William Atkins „Podstawy chemii fizycznej”

1

---