Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej
Nazwisko i imię Huk Tomasz studenta:							Symbol grupy MD 103.1c
Data wykonania ćwiczenia:		Symbol ćwiczenia: 1.2	Temat zadania: Pomiar współczynnika załamania światła przy pomocy mikroskopu.
Zaliczenie:			Ocena:	Data:	Podpis

1. WYNIKI POMIARÓW I OBLICZEŃ

tabelka

Lp.	Położenie początkowe	Ilość obrotów	Położenie końcowe	h [mm]	h śr. [mm]	d [mm]	n śr.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.	9	24 22 23 21 21 21 21 22 22 23 21 21	1,4 1,5 1,2 1,4 1,2 1,8 1,6 2,0 1,6 1,9 1,4 1,7	2,424 2,225 2,322 2,124 2,122 2,128 2,126 2,230 2,226 2,329 2,124 2,127	2,209	3,151 3,151 3,156 3,151 3,161 3,151 3,156 3,156 3,156 3,151 3,161 3,156	1,428
				=26,507		=37,857 d śr=3,155

2. Przykładowe obliczenie wyników:

h1=24*0,1[mm]+(1+1,4)*0,01[mm]=2,4[mm]+0,024[mm]=2,424[mm]

h2=22*0,1[mm]+(1+1,5)*0,01[mm]=2,2[mm]+0,025[mm]=2,225[mm]

h3=2,3[mm]+0,022[mm]=2,322[mm]

h4=2,1[mm]+0,024[mm]=2,124[mm]

h5=2,1[mm]+0,022[mm]= 2,122[mm]

h6=2,1[mm]+0,028[mm]= 2,128[mm]

h7=2,1[mm]+0,026[mm]= 2,126[mm]

h8=2,2[mm+]0,030[mm]= 2,230[mm]

h9=2,2[mm]+0,026[mm]= 2,226[mm]

h10=2,3[mm]+0,029[mm]= 2,329[mm]

h11=2,1[mm]+0,024[mm]= 2,124[mm]

h12=2,1[mm]+0,027[mm]= 2,127[mm]

n śr.= d śr / h śr= 3,155[mm] / 2,209[mm]=1,428[mm]

3. KRÓTKA TEORIA

Falą nazywamy zaburzenie mechaniczne lub elektromagnetyczne rozchodzące się w czasie i przestrzeni z określoną prędkością, charakterystyczną dla danego rodzaju fal i ośrodka, w którym fale się rozchodzą.

Jeżeli wybraną cząstkę jednowymiarowego ciągłego ośrodka materialnego pobudzimy w dowolny sposób do drgań harmonicznych, to jej drgania można opisać równaniem: y = A sin ( ω t ) , gdzie y jest wielkością wychylenia cząstki z położenia równowagi, A - amplituda drgań ( największym wychyleniem ), ω - częstością kołową, t - czasem, natomiast ωt fazą drgań.

Drgania te będą się przenosić na cząstki sąsiednie. Wielkość opóźnienia będzie proporcjonalna do odległości x tych cząstek od cząstki pierwotnej ( źródła fali ). Równanie ruchu dla tych cząstek przyjmuje więc następującą postać: y = A sin ( ωt - kx ). Odległość pomiędzy punktami ośrodka, dla których różnica faz wynosi 2Π stanowi długość fali i oznaczamy ją symbolem - λ . Jeżeli więc ( ωt - kx1 ) - ( ωt - kx2 ) = 2Π, to x2 - x1 = λ.

Podstawiając tak określoną wielkość k do równania y = A sin ( ωt - kx ) oraz przyjmując, że ω = 2Π / T

( T - okres drgań ) otrzymamy: y = A sin 2Π . Jest to równanie dla przypadku jednowymiarowego.

Niektóre zjawiska związane z ruchem falowym można wyjaśnić w oparciu o zasadę Huygensa, według której każdy punkt, do którego dociera czoło fali, można traktować jako źródło fali kulistej, tzw. elementarnej fali cząstkowej.

Rozpatrzmy przypadek, gdy fala płaska przechodzi z jednego ośrodka do drugiego, przy założeniu, że prędkości fali

w obu ośrodkach są różne i wynoszą: w ośrodku I - v1, a w ośrodku II - v2 ( v1 > v2 ); odpowiadające im długości fali są λ1 i λ2.

S S

S1 S1

B

I

A C

II

D

S2 S2

Przyjmując, że kierunki SA i SC rozchodzenia się fali padającej tworzą kąt α z prostą prostopadłą do powierzchni rozgraniczającej ośrodki. Na granicy ośrodków fala zostanie częściowo odbita w kierunku prostych AS1 i CS1, częściowo przejdzie do drugiego ośrodka i będzie rozchodzić się w kierunkach AS2 i CS2. W czasie Δt, w przeciągu którego fala w ośrodku I rozejdzie się na odległość BC = v1 *Δt, w środku II z punktu A rozejdzie się na odległość AD = v2 * Δt. Z punktów pośrednich, leżących pomiędzy A i C, też rozejdą się fale cząstkowe - oczywiście na odległość odpowiednio mniejsze. Czoło fali rozchodzącej się w ośrodku II, stanowi obwiednię fal elementarnych, będzie płaszczyzną. To oznacza, że po przejściu granicy dwu ośrodków fala płaska pozostaje falą płaską. W związku z założeniem, że v1 ≠ v2 promien fali rozchodzącej się w ośrodku II, będzie tworzył z normalną do powierzchni rozgraniczającej β ≠ α. Kąt β nazywamy kątem załamania fali. Z konstrukcji geometrycznej przedstawionej na rysunku wynika, że

AC * sin α = BC = v1 * Δt = λ1

oraz AC * sin β = AD = v2 * Δt = λ2

Dzieląc stronami równanie pierwsze przez drugie otrzymamy 21 . A więc stosunek sinusa kąta padania do sinusa kąta załamania fali, dla danych dwu ośrodków, jest wielkością stałą i równą stosunkowi prędkości fali w tych ośrodkach. Wielkość tę oznaczamy przez n21 i nosi ona nazwę współczynnika załamania ośrodka drugiego względem pierwszego. W oparciu o zasadę Huygensa można wykazać, że α = α`, oraz że promień padający , promień odbity i normalna w punkcie padania leżą w jednej płaszczyźnie. Formuła ta stanowi prawo odbicia fali.

4. OPIS WYKONANIA ĆWICZENIA

Zjawisko załamania światła wywołuje pewne złudzenie przy oglądaniu przedmiotów wtedy, gdy przedmiot i obserwator znajdują się w dwu oddzielnych ośrodkach, o różnych współczynnikach załamania światła. Rozpatrzmy obraz jaki widzi obserwator oglądający dno płytki o grubości d umieszczonej w powietrzu. Dla znalezienia obrazu punktu O wystarczy określić bieg dwu promieni wychodzących z tego samego punktu pod pewnym kątem.

A B Przejście promienia przez płytkę

płasko-równoległą.

h

O1

d

O

5. RACHUNEK BŁĘDÓW

Błąd względny maksymalny pomiaru;

δm(n) = + Δdm = niedokładność odczytu ze śruby Δhm = 2*(Δh1 + Δh2)

Δdm = 0,01 [m]*10

Δh1 = 0,002 [m]*10

Δh2 = 0,004 [m]*10

Δhm = 2*( 0,002 + 0,004 ) = 0,016 [m]*10

δm (n) =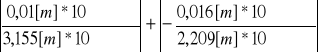
= 0,0032 + 0,0072 = 0,0104

procentowo: 0,0104*100% = 1,04%

Błąd bezpośredni maksymalny:

Δn = 0,0104*1,428 = 0,015

Wynik pomiaru zapisujemy: n = 1,428 ± 0,015

1,413 < n < 1,443

lp	h [mm]	h śr. [mm]	d [mm]	d śr. [mm]	r =h- [mm]	r =d - [mm]	r [mm ]	r [mm ]
1	2,424 2,225 2,322 2,124 2,122 2,128 2,126 2,230 2,226 2,329 2,124 2,127	2,209	3,151 3,151 3,156 3,151 3,161 3,151 3,156 3,156 3,156 3,151 3,161 3,156	3,155	0,215	-0,004	0,046225	0,000016
2									0,016	-0,004	0,000256	0,000016
3									0,113	0,001	0,012769	0,000001
4									-0,085	-0,004	0,007225	0,000016
5									-0,087	0,006	0,007569	0,000036
6									-0,081	-0,004	0,006561	0,000016
7									-0,083	0,001	0,006889	0,000001
8									0,021	0,001	0,000441	0,000001
9									0,017	0,001	0,000289	0,000001
10									0,12	-0,004	0,0144	0,000016
11									-0,085	0,006	0,007225	0,000036
12									-0,082	0,001	0,006724	0,000001
	=26,507		=37,857				=0,116573	=0,000157

Średnie błędy kwadratowe pojedynczego pomiaru (odchylenia standardowe)

=
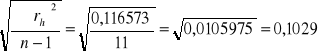
mm

=
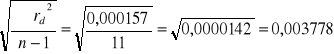
mm

3
=0,3087-więc wszystkie r
< 3

3
=0,0113337 -więc wszystkie r
< 3

wszystkie pomiary spełniają kryterium trzysigmowe dokładności, a więc bezpośrednie pomiary d i h nie są obarczone błędami grubymi,

• średnie błędy kwadratowe średnich arytmetycznych

=
0,029705 mm

=
0,010906 mm

Średni błąd kwadratowy pomiaru wielkości n:

+
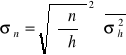
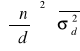
,gdzie funkcja n dana jest wzorem : n =

=

=

Wynik pomiaru wielkości fizycznej n zapiszemy:

- przy kryterium jednosigmowym n =


+

1,428 - 0,02
1,428+0,02

1,408
1,448

Oznacza to że w podanym przedziale można oczekiwać wartości rzeczywistej

z prawdopodobieństwem 68,3%

stosując kryterium trzysigmowe otrzymamy: n =


+3

1,428 - 0,06
1,428+0,06

1,368
1,488

Oznacza to że w podanym przedziale można oczekiwać wartości rzeczywistej

z prawdopodobieństwem 99,7%

Można również obliczyć:

-błąd względny pomiaru

błąd przeciętny: p
= 0,013352

• błąd prawdopodobny:
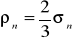
  = 0,01113

---