I. Cel ćwiczenia

Celem ćwiczenia jest dokładne zapoznanie się ze zjawiskiem występowania indukcyjności własnej oraz wzajemnej uzwojeń, podstawowymi prawami nim rządzącymi, a także metodami wyznaczania podstawowych parametrów w obwodach, w których ów zjawisko występuje.

II. Wprowadzenie teoretyczne

Indukcyjność określa zdolność obwodu do wytwarzania strumienia pola magnetycznego Φ powstającego w wyniku przepływu przez obwód prądu elektrycznego I. Oznaczana jest symbolem L. Jednostką indukcyjności jest henr [H]. Ze strumieniem indukcji magnetycznej Φ i natężeniem prądu I związana jest wzorem:

Każda zmiana strumienia obejmowanego przez obwód, także tego wytworzonego przez ten obwód, wywołuje powstanie siły elektromotorycznej indukcji:

Tę właściwość obwodów nazywa się samoindukcją. Zatem indukcyjność ma wpływ na wartość siły elektromotorycznej indukcji.

1) Indukcyjność pod nieobecność ferromagnetyków

Gdy w otoczeniu obwodu nie ma żadnych ciał o właściwościach ferromagnetycznych, czyli przenikalność magnetyczna ośrodka μ jest równa 1 (w próżni) lub μ > 1 ale stałe, wówczas indukcyjność w równaniu
jest współczynnikiem proporcjonalności. W takim przypadku indukcyjność jest stała i zależy tylko od geometrii obwodu. Siła elektromotoryczna indukcji jest wówczas proporcjonalna do prędkości zmian natężenia prądu elektrycznego:

2) Indukcyjność w obecności ferromagnetyków

Obecność ferromagnetyka w otoczeniu przewodnika z prądem powoduje nieliniowe złożone zmiany przenikalności magnetycznej. Zmiana natężenia prądu powoduje zmianę natężenia pola magnetycznego, co z kolei powoduje zmianę przenikalności magnetycznej. Oznacza to, że indukcyjność przewodnika z prądem jest wówczas funkcją natężenia prądu płynącego w tym przewodniku:

Zależność siły elektromotorycznej indukcji od zmian natężenia prądu przybiera postać:

lub

III. Rozpatrywane zagadnienia

1) Indukcyjność nieskończenie długiego przewodnika prostoliniowego;

2) Indukcyjność wzajemna dwóch cewek nawiniętych na wspólnym rdzeniu;

3) Indukcyjność własna oraz wzajemna dwóch cewek nawiniętych na wspólnym

rdzeniu (obwód magnetyczny zamknięty, rozgałęziony);

Ad 2) Indukcyjność wzajemna dwóch cewek nawiniętych na wspólnym rdzeniu

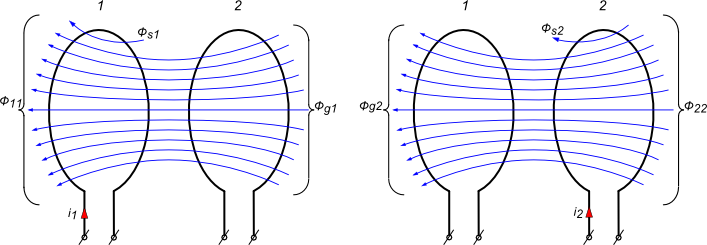
W celu uproszczenia dalszych rozważań wyprowadźmy podstawowe wielkości dla sprzężenia dwóch cewek bez rdzenia.

Prąd przepływa przez element 1 Prąd przepływa przez element 2

- strumień rozproszenia cewki pierwszej;

- strumień główny cewki pierwszej;

- całkowity strumień magnetyczny cewki pierwszej;

Analogicznie dla przypadku drugiego.

Jeżeli mają po z zwojów, to wprowadzamy pojęcie strumienia skojarzonego:

całkowite strumienie

skojarzone;

strumienie skojarzone zależne tylko od strumieni głównych

skojarzone z różnymi elementami;

strumienie skojarzone od

strumieni rozproszenia;

strumienie skojarzone zależne od strumieni głównych

skojarzone z tym samym elementem;

Indukcyjności własne:

Indukcyjności wzajemne:

Stosunek strumienia głównego do strumienia całkowitego nazywamy współczynnikiem sprzężenia elementu pierwszego z drugim (i na odwrót):

Współczynnikiem sprzężenia obu elementów określamy jako średnią geometryczną współczynników k₁ oraz k₂:

Mnożąc przez siebie indukcyjności własne L₁ oraz L₂ w rezultacie otrzymujemy:

Wyprowadzenie jednostki:

Przejdźmy teraz do układu dwóch cewek nawiniętych na wspólnym rdzeniu

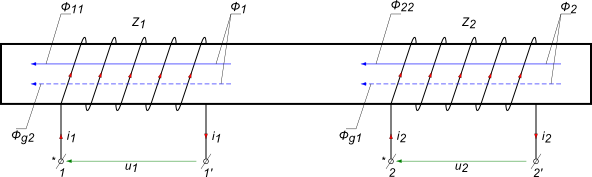
Jeżeli cewki znajdują się w ośrodku o takiej samej przenikalności magnetycznej, to:

Ad 3) Indukcyjność własna oraz wzajemna dwóch cewek nawiniętych na wspólnym

rdzeniu (obwód magnetyczny zamknięty, rozgałęziony);

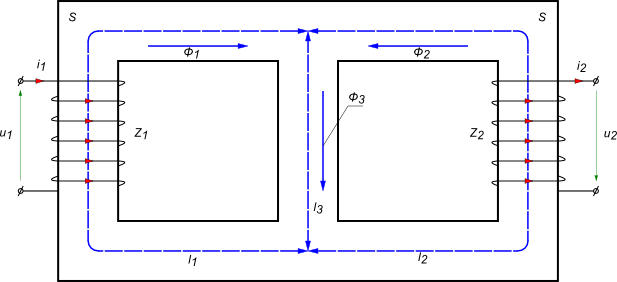
Schemat zastępczy obwodu magnetycznego

Literatura:

[1] Baron Bernard, Spałek Dariusz, „Wybrane problemy z teorii pola elektromagnetycznego”,

Wydawnictwo Politechniki Śląskiej, Gliwice 2006

[2] Szulkin Paweł, Pogorzelski Seweryn, „Podstawy teorii pola elektromagnetycznego”,

Wydawnictwo Naukowo-Techniczne, Warszawa 1964

[3] Bolkowski Stanisław, „Elektrotechnika”, WSiP, Warszawa 2005

[4] Bolkowski Stanisław, „Elektrotechnika teoretyczna Tom 1”, Wydawnictwa Naukowo-Techniczne,

Warszawa 1982

[5] Janeczek Andrzej, artykuł w Elektronika dla wszystkich, „Jak określić indukcyjność cewek, część 2”,

numer: Czerwiec 2003

[6] www.wikipedia.org (http://pl.wikipedia.org/wiki/Indukcyjność)

po podstawieniu

po podstawieniu

tak więc:

---