Przykładowe zadania zaliczeniowe

Teoria Pola

1.1. Obliczyć
oraz
pól wektorowych:

a)

b)
(współrzędne sferyczne)

1.2. Dane pole skalarne

Obliczyć wektor

2.1. Obliczyć strumień wektora
przez powierzchnię kuli o środku w punkcie P(0,0,0) i promieniu
.(tw. Gaussa)

Czy zmiana położenia punktu P spowoduje zmianę tego strumienia?

2.2. Obliczyć cyrkulację wektora
po drodze wyznaczonej przez boki prostokąta o długościach odpowiednio a i b. Jeden z boków a leży na osi x natomiast jeden z boków b na osi y. (tw. Stokes'a)

3.1.Wyznaczyć wartości iloczynu wektorowego i skalarnego pary wektorów:

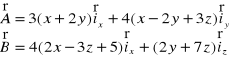
w punkcie P(0,1,-1)

3.2. Wyznaczyć wartości iloczynu wektorowego i skalarnego pary wektorów:

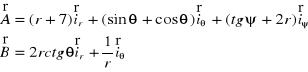
(współrzędne sferyczne)

w punkcie P(1; π/3; π/4)

4.1. Płaszczyzna z=0 jest granicą dwóch ośrodków:

W pierwszym ośrodku przy granicy wektor

Wyznaczyć miary wektorów
przy granicy ośrodków, jeżeli nie płyną prądy powierzchniowe.

Wskazówka: wyodrębnić składowe styczne wektora H i składowe normalne wektora B, które zachowują ciągłość.

5. Dany obwód magnetyczny ze szczeliną powietrzną (rysunek 1)

z uzwojeniem wzbudzającym n=500 zwojów. Wyznaczyć wartość prądu i w uzwojeniu, aby osiągnąć zadaną wartość indukcji magnetycznej w szczelinie B₀=0,4T.

Dane:
Charakterystyka magnesowania rdzenia ferromagnetycznego:

B[T]	0	0,1	0,4	0,6	0,8	0,9	1,0	1,2	1,35	1,5	1,6
H[A/cm]	0	0,7	1,2	1,5	2,0	2,8	3.6	6,75	12,3	21,9	30

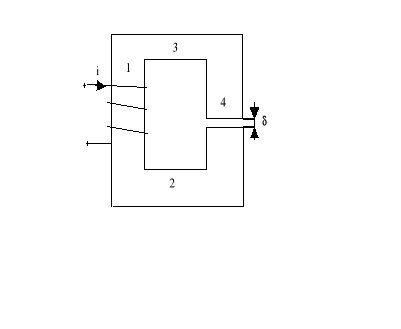
Rys.1

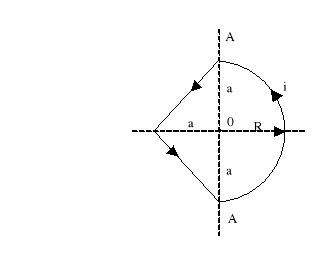
6. Wyznaczyć wartość natężenia pola magnetycznego H w punkcie 0 ramki (rysunek 2), jeżeli:
. Jak zmieni się ta wartość, jeżeli część łukowa ramki zostanie zgięta względem osi A-A o kąt γ

a)γ=90⁰; b) γ=180⁰.

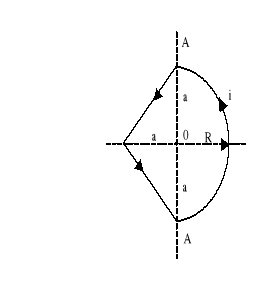
Rys.2

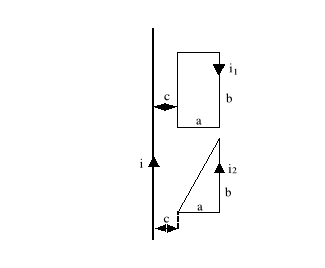
7. Wyznaczyć strumienie magnetyczne przenikające obie ramki, od pola prądu i płynącego w długim przewodzie (rysunek 3)

Dane:

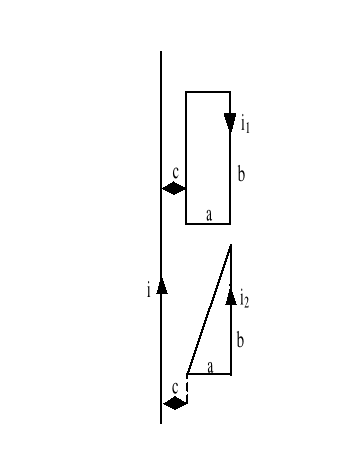
Rys.3

8. Wyznaczyć wartości sił działających na wszystkie boki ramek z p.7

od pola prądu i jeżeli i₁=100A; i₂=200A.