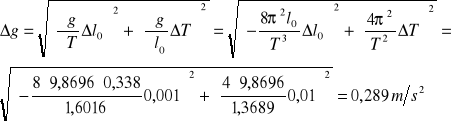![]()
Widać więc, że nie ma ona istotnego wpływu na wielkość okresu.
WEAiIE |
Biegański Marek Madej Marek |
Grupa I |
Zespół 11 |
|||
Laboratorium Fizyczne |
Temat: Wahadło rewersyjne |
Nr ćwiczenia: 3 |
||||
Data wykonania: 18.03.1999 |
Data oddania:
25.03.1999 |
Zwrot do poprawy: |
Data odbioru: |
Data zaliczenia: |
Ocena: |
|
1. Cel ćwiczenia
Celem ćwiczenia jest wyznaczenie przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego.
2. Wprowadzenie teoretyczne
Najprościej przyspieszenie ziemskie można obliczyć ze związku dla wahadła matematycznego:
Ponieważ jednak w realnym doświadczeniu mamy do czynienia raczej z wahadłem fizycznym przyspieszenie byłoby obarczone zbyt dużym błędem metodycznym.
Wychodzimy więc od ogólnego równania ruchu bryły sztywnej:
oraz jego rozwiązania (przyjmując przybliżenia sinϕ=ϕ)
gdzie
czyli
Ze wzoru widać że przy zastosowaniu metody wykorzystującej ten związek pojawiają się trudności z bezpośrednim, wystarczającym pomiarem.
Istnieje jednak inna metoda pozwalająca na korzystanie ze wzoru (nie bezpośrednio). Szukamy dwóch osi obrotu, równoległych do siebie i leżących na jednej prostej przechodzącej przez środek ciężkości , których okresy są równe.
Otrzymujemy następujące związki:
lub wykorzystując twierdzenie Steinera:
Stąd, że T1 i T2 są równe zapisujemy
=
czyli
(b-a)(Is-m a b)=0
Czyli T1 = T2, gdy O2 obierzemy w odległości b=a lub gdy O2 obierzemy w odległości takiej że :
W sytuacji (I) o okresach nie możemy powiedzieć nic ciekawego oprócz tego, że są równe, natomiast w sytuacji (II) z i otrzymujemy :
Oznaczając odległość między osiami O1 i O2 przez lo=a+b
oraz T1 = T2 = T0 , mamy ostatecznie:
Aby doświadczalnie wyznaczyć dwie osie o równych okresach wykorzystujemy silnie asymetryczne wahadło rewersyjne, by wyeliminować sytuację, że a=b.
3. Wyniki pomiarów i ich opracowanie
Pomiary wykonywane były dla 50 wahnięć wahadła.
l0 = 0.338m0.001m - odległość między osiami wahadła,
Δts = 0,5 s - szacowany błąd odczytu czasu wynikający z niedoskonałości zmysłów ludzkich.
θm = 0,03 rad - szacowana wartość kąta maksymalnego wychylenia wahadła (obliczona z amplitudy (1 cm) i długości wahadła).
Położenie ciężarka |
Czas wahań - pierwsza oś |
Czas wahań - druga oś |
x [cm] |
t1 [s] |
t2 [s] |
2 |
61,34 |
59,00 |
4 |
58,66 |
58,61 |
6 |
57,22 |
57,88 |
8 |
56,14 |
57,57 |
10 |
55,41 |
57,56 |
12 |
54,82 |
57,53 |
14 |
55,07 |
57,41 |
16 |
55,32 |
57,35 |
18 |
56,05 |
57,43 |
20 |
56,67 |
57,67 |
22 |
57,31 |
57,97 |
24 |
57,86 |
58,46 |
25 |
58,62 |
58,46 |
|
59,23 |
58,83 |
Wykresy zależności t(x) przecięły się dla t1=58,45 s ± 0,5 s oraz t2 = 58,35 s ± 0,5 s.
Średnia wynosi więc 58,40 s ± 0,5 s.
Szukany okres jest 50 razy mniejszy od znalezionej średniej i ma wartość T = 1,17 ± 0,01 s.
Wartość poprawki uwzględniającej skończoną wartość kątów wychyleń wynosi:
![]()
Widać więc, że nie ma ona istotnego wpływu na wielkość okresu.
Przyspieszenie ziemskie obliczamy po przekształceniu wzoru :
![]()
Wynik ten obarczony jest błędem o wartości:
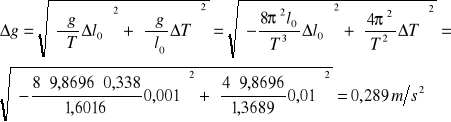
Znaleziona wartość przyspieszenia wynosi więc 9,75 m/s2 ± 0,289 m/s2 .
4. Wnioski
Obliczona wartość przyśpieszenia jest w granicach błędu zgodna z wartością tablicową. Duży błąd pomiaru czasu wynika z bezwładności włączania i wyłączania stopera, gdy wahadło znajduje się w granicznych położeniach, co spowodowane jest niedoskonałością zmysłów ludzkich. Do pomiaru czasu nie jest uwzględniony opór powietrza jako czynnik hamujący wahadło, który to z kolei powoduje stopniowe zmniejszenie amplitudy i w konsekwencji skrócenie czasu pomiaru. Biorąc jednak pod uwagę masę wahadła można pominąć ten błąd bez skutków negatywnych na wynik.
- 3 -
![]()
![]()