EAIiE	Imię Nazwisko: 1.Tomasz Boryło		Rok: II		Grupa:		Zespół:
Pracownia fizyczna I	Temat: Mostek Wheatstone'a						Nr ćwiczenia: 32
Data wykon: 28.10.1999	Data oddania:	Zwrot do pop:		Data oddania:		Data zalicz:	Ocena:

Mostek Wheatstone'a jest układem do pomiaru (porównywania) oporów. Tworzy go połączenie czterech oprorów: R_x, R₂, R₃,R₄ oraz galwanometru o oporze R₅. Mostek jest zasilany z ogniwa galwanicznego lub zasilacza. (rys.1).

Rys. 1

Niech I oznacza natężenie prądu p.łynącego z ogniwa, a natężenia prądów w odcinkach obwodu AB, AD, BC, DC, i BGD odpowiednio: I₁, I₂, I₃, I₄, I₅. W układzie są 4 węzły A, B, C, D. Dla trzech z nich układa się równania Kirchoffa. Jeśli kierunek prądu kest taki, jak wskazują strzałki, dla węzłów A, B i D otrzymujemy:

A: I - I₁ - I₃ = 0
B: I₁ - I₂ -I₅ = 0 (1)
D: I₅ +I₃ -I₄ = 0

Drugi układ równań Kirchoffa można ułożyć wydzielając w schemacie zamknięte obwody ABDA, BCDB i ACEA. Obchodząc każdy z tych obwodów według kierunku wskazówek zegara otrzymujemy dla obwodu:

ABDA: I₅R_x + I₅R₅ - I₃R₃ = 0
BCDB: I₂R₂ + I₄R₄ - I₅R₅ = 0 (2)
ACEA: I₃R₃ + I₄R₄ + IR_E = 

Jeśli dana jest siła elektromotoryczna  oraz opory R₂, R₃,R₄ i R_E, można znaleźć natężenia wszystkich sześciu prądów I, I₁, I₂, I₃, I₄, I₅.

Metoda Wheatstone'a porównywania oporów polega na tzw. równoważeniu mostka, to znaczy na takim dopasowaniu oporów, by potencjały w punktach B i D były równe (V_B = V_D), czyli żeby prąd p.łynący przez galwanometr G był równy zeru. Przy I₅ = 0 drugie i trzecie równanie układu (1) dają:

Rys. 2

I₂ = I₁ I₃ = I₄ (3)

a pierwsze i drugie równanie układu (2)

I₁R_x = I₃R₃ I₂R₂ ­= I₄R₄. (4)

Z równań (3) i (4) wynika, że

Ostatnie wyrażenie pozwala eksperymentalnie wyznaczyć R_x.

Mostek Wheatstone'a używany w ćwiczeniu przedstawiono na rysunku 2. Prąd płynący z ogniwa galwanicznego E rozgałęzia się w punkcie A. Jedna jego część płynie przez szeregowo połączone opory R_x i R₂, druga przez przewód AC. Przez zmiany położenia punktu D zmienia się stosunek oporów R₃ do R₄. Na odcinku BGD prąd nie będzie płynął, jeżeli

Ponieważ R_AD i R_DC są oporami odcinków tego samego jednorodnego drutu, ich wielkości są proporcjonalne do długości:

Ponadto b jest różnicą całkowitej długości drutu l i odległości a, b=l-a. Ostatecznie otrzymujemy:

(4)

Dokładność pomiaru mostkiem Wheatstone'a z drutem oporowym zależy przede wszystkim od błędu wyznaczenia odległości a. Zgodnie z prawem przenoszenia błędu:

(5)

Tak więc błąd pomaiaru będzie najmniejszy gdy pochodna wyrażenia (5) będzie równa 0:

Rozwiązanie a=1/2 l odpowiada po uwzględnieniu drugiej pochodnej minimalnej wartości błędu. Tak więc aby pomiar był najdokładniejszy należy tak dobrać opór R₂, aby stan równowagi mostka można było uzyskać w przybliżeniu w połowie długości drutu oporowego.

Opracowanie wyników.

A - Mostek oporowy.

a,R₂ - wartości zmierzone

Wyznaczenie R_x1.

A [cm]	R2	Rx1 [
50	13	13,00
48,1	14	12,97
53,1	12	13,59
	Mediana:	13,00

Błąd dla wartości R­_x1: ±0,21

Wyznaczenie R_x2

A [cm]	R2	Rx2 [
50,6	20	20,48
49,4	21	20,50
48,2	22	20,47
	Mediana:	20,48

Błąd pomiaru wartości R_x2: ±0,01

Wyznaczenie oporu rezystorów połączonych szeregowo:

A [cm]	R2	Rx1+Rx2 [
48,2	33	30,71
47,5	34	30,76
49,0	32	30,74
	Mediana:	30,74

Błąd: ±0,02

Wyznaczenie oporu rezystorów połączonych równolegle:

A [cm]	R2	Rx1+Rx2 [
49,5	7	6,86
53,4	6	6,87
46,1	8	6,84
	Mediana:	6,86

Błąd: ±0,01

Zestawienie wyników pomiarów.

Rx1 []	13,00
Rx2 []	20,48
Rx1+Rx2 (szeregowo) []	30,74
Rx1+Rx2 (równolegle) []	6,86

Porównanie wyników z danymi teoretycznymi:

Porównujemy wartości średnie wyznaczonych doświadczalnie oporów zastępczych dla połączenia równoległego i szeregowego dla oporów Rx1 i Rx2.

	R obliczone []	Rśr dośw []
Równolegle	7,95	6,86
Szeregowe	33,48	30,74

2. Wyznaczenie krzywej rozkładu.

Przedział		Liczba
Rśr-3σ - Rśr-2σ	23,44 - 25,29	1
Rśr-2σ - Rśr-σ	25,29 - 27,13	1
Rśr-σ - Rśr	27,13 - 28,98	5
Rśr - Rśr+σ	28,98 - 30,83	88
Rśr+σ - Rśr+2σ	30,83 - 32,68	1
Rśr+2σ - Rśr+3σ	32,68 - 34,53	0

odchylenie standardowe :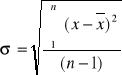
=1,85

wartość średnia ze stu pomiarów: 29,98

Histogram.

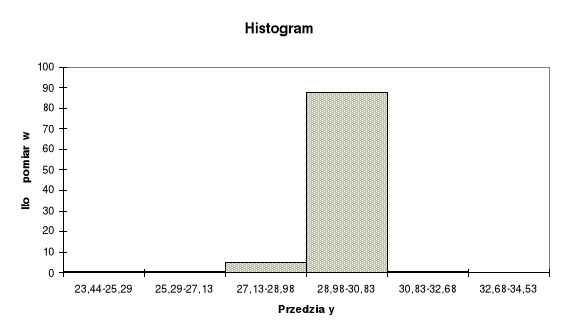
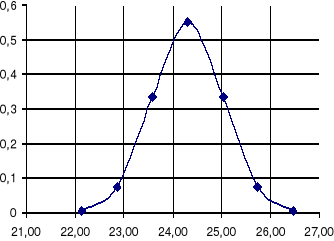
Porównanie z wartościami teoretycznymi dla rozkładu Gaussa.

Wartości teoretyczne dla punktów granicznych przedziałów obliczone ze wzoru:

R	(x)
23,44	0,006134
25,29	0,074729
27,13	0,334911
28,98	0,552174
30,83	0,334911
32,68	0,074729
34,53	0,006134

Komentarz do obliczeń

Wartość mierzonego oporu liczyłem według wzoru (4) [wstęp teoretyczny], natomiast błąd dla małej liczby pomiarów liczyłem z wzoru:

Gdzie: R - rozstęp (różnica max -min)

d = 1,693 (dla 3 pomiarów wzięte z tablic)

n - liczba pomiarów (w tym wypadku n=3)

Wnioski

Widzimy, ze w porównaniu pomiarów otrzymanych z doświadczenia i wyliczonych teoretycznie dla rezystorów połączonych równolegle i szeregowo nieznacznie się różni. Może być to spowodowane tym iż nasza metoda nie była super dokładna, a poza tym nasze obliczenia teoretyczne opierały się o wartość rezystancji policzonej wcześniej tą samą metodą.

Dokonałem także pomiaru oporu jednego z oporników sto razy i na podstawie wyników wykreśliłem rozkład Gaussa. Cztery wyniki ze stu nie zawarły się w przedziale +/- σ mogło to być spowodowane błędem odczytu z podziałki lub złym zrównoważeniem mostka.

---