Wydział EAIiE |
|
Rok pierwszy |
Grupa III |
Zespół : 6 |
|||
Pracownia fizyczna I |
Temat: Przenikalność dielektryczna |
Nr ćwiczenia : 33 |
|||||
Data wykonania: 5.05.99 |
Data oddania: |
Zwrot do popr. |
Data oddania: |
Data zaliczenia: |
Ocena: |
||
Cel ćwiczenia.
Pomiar pojemności kondensatorów powietrznych i z warstwą dielektryka w celu wyznaczenia przenikalności dielektrycznej próżni ε0 i przenikalności względnych εr różnych materiałów.
Wprowadzenie.
Kondensator jest układem przewodników oddzielonych warstwą izolatora. Przez pojemność kondensatora C rozumiemy stosunek ładunku Q do napięcia między okładkami U,
![]()
Przy pomocy prawa Gaussa wyprowadza się, że pojemność kondensatora płaskiego wynosi
![]()
gdzie S jest powierzchnią okładki, d odległością między okładkami, współczynnik ε0 = 8,85 pF/m nosi nazwę przenikalności dielektrycznej próżni i εr jest względną przenikalnością dielektryczną materiału między okładkami kondensatora.
Ze wzoru ![]()
wynika, że dla wyznaczenia stałych ε0 i εr należy zmierzyć pojemność kondensatorów o znanych wymiarach geometrycznych, próżniowego i wypełnionego dielektrykiem.
1) Wyznaczenie przenikalności dielektrycznej próżni ε0
W naszym eksperymencie przybliżeniem kondensatora próżniowego jest kondensator powietrzny (rys.1). Okładkami kondensatora są kołowe płyty metalowe. Określoną odległość między płytami uzyskuje się przez umieszczenie w trzech miejscach stosu izolujących krążków. Do pomiaru pojemności kondensatora stosujemy cyfrowy miernik pojemności.
Wartości ε0 nie możemy wyznaczyć wprost ze wzoru ![]()
z dwóch powodów. Po pierwsze krążki określające odległość d między płytami wykonane są z materiału o przenikalności dielektrycznej εr znacznie większej od jedności, co powoduje powiększenie całkowitej pojemności kondensatora. Kondensator nasz potraktować można jako równoległe połączenie kondensatora z dielektrykiem o przenikalności względnej εr i łącznej powierzchni okładek równej 3Sp (gdzie Sp jest powierzchnią jednego krążka) oraz kondensatora próżniowego, o powierzchni okładek równej S-3Sp.
Pojemność całkowita wynosi:
![]()
Z uwzględnieniem tej poprawki wartość ε0 obliczamy jako:
![]()
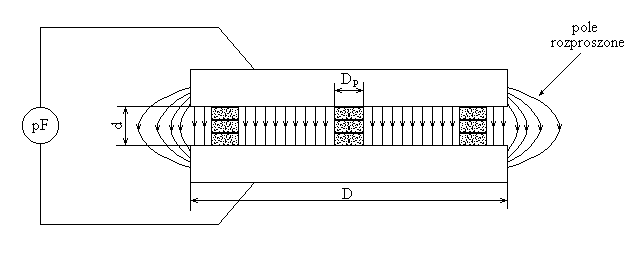
Rys.1. Pole elektryczne w kondensatorze płaskim
Druga istotna poprawka wynika z istnienia tzw. pola rozproszonego. Wzór ![]()
jest w istocie wzorem przybliżonym. Jego wyprowadzenie przy użyciu prawa Gaussa opiera się na upraszczającym założeniu, że pole E ma wartość stałą we wnętrzu kondensatora i raptownie znika poza jego krawędzią. Z samych praw elektrostatyki wynika, że poza brzegami kondensatora pole nie może raptownie znikać. Niejednorodne (o zakrzywionych liniach sił) pole elektryczne poza okładkami nosi nazwę pola rozproszonego. Powoduje ono dodatkowy wzrost pojemności kondensatora, w konsekwencji wartość ε0 wyliczona wprost ze wzoru ![]()
byłaby zawyżona.
Dla danej geometrii płyt odpowiednią poprawkę można obliczyć przez numeryczne obliczenie rozkładu pola przy brzegu kondensatora. W naszym ćwiczeniu zastosujemy doświadczalny sposób eliminacji wpływu pola rozproszonego. Efektywna „objętość” pola rozproszonego jest rzędu 2Πrd2 gdyż pole to zajmuje z grubsza pas wysoki i szeroki na d wokół obwodu kołowych płyt kondensatora. Natomiast objętość pola jednorodnego wewnątrz kondensatora wynosi Πr2d. Względny udział pola rozproszonego, będący stosunkiem tych objętości wynosi 2d/r, czyli że maleje do zera w granicy d → 0.
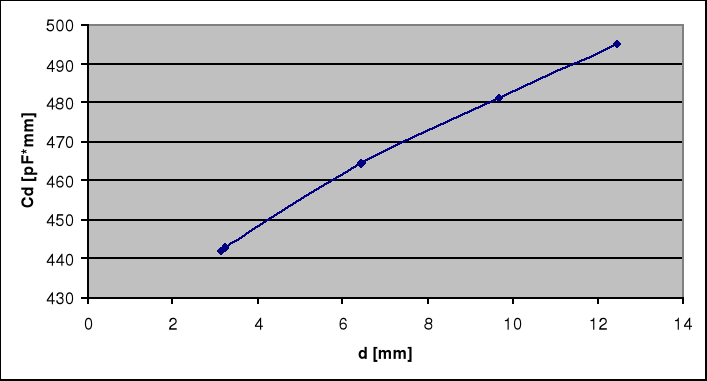
Wykonamy zatem serię pomiarów pojemności C dla różnych wartości d, a następnie wykres iloczynu Cd w funkcji grubości d (rys.2).
Przez uzyskane punkty wykresu przeprowadzimy graficznie lub analitycznie gładką krzywą i ekstrapolujemy czyli przedłużamy do wartości d = 0. Ekstrapolowana wartość iloczynu Cd - czyli współrzędną punktu przecięcia krzywej Cd = f(d) z osią pionową podstawiamy do licznika wzoru ![]()
by uzyskać poprawną wartość ε0.
Trzecim potencjalnym źródłem błędu systematycznego przy wyznaczaniu przenikalności dielektrycznej próżni jest fakt, że zamiast kondensatora próżniowego mamy kondensator wypełniony powietrzem.
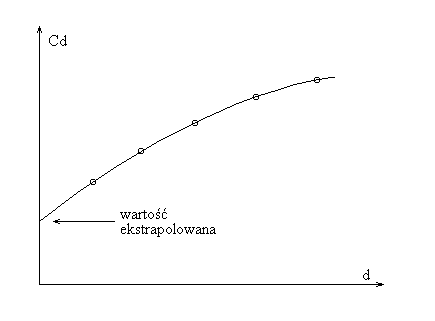
Rys.2. Metoda eliminacji wpływu pola rozproszonego
2) Pomiar przenikalności względnej dielektryków.
Wartość εr dielektryków stałych wyznaczyć można przez pomiar pojemności kondensatora płaskiego z okładkami oddzielonymi cienką płytą z badanego materiału. Korzystamy ze wzoru ![]()
, poprawki na pole rozproszone nie będziemy uwzględniać.
Rys.3. Kabel koncentryczny jako kondensator cylindryczny.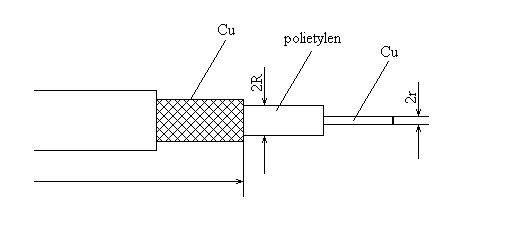
Obok kondensatora płaskiego przykładem obiektu o określonej pojemności jest kabel koncentryczny (rys.3). Można go traktować jako kondensator cylindryczny, którego jedną okładką jest środkowy drut, drugą - miedziany oplot. Pojemność kondensatora cylindrycznego wyraża wzór:
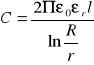
,
w którym R i r oznaczają promienie okładek kondensatora, l jest jego długością.
Pojemność kabla koncentrycznego, zwykle wyrażana w pF/m, jest parametrem, który może mieć znaczenie dla działania współpracujących układów elektronicznych. Jej pomiar umożliwia wyznaczenie εr dla stosowanego w nim dielektryka, którym zwykle jest polietylen.
3) Wyznaczenie ε0 jako pośredni pomiar prędkości światła.
W równaniach elektrostatyki (prawo Gaussa) pojawia się stała ε0 natomiast w równaniach magnetostatyki (prawo Ampera) stała μ0. Można odnieść wrażenie, że scharakteryzowanie własności elektromagnetycznych próżni wymaga dwóch stałych. Tak jednak nie jest, gdyż wartość jednej z nich, konkretnie μ0 w układzie SI, jest wynikiem konwencji definiującej jednostkę prądu.
Przypomnijmy sobie, że amper jest zdefiniowany jako wartość prądu, który płynąc przez dwa nieskończone równoległe przewody odległe o a=1 m wytwarza siłę F=2*10-7N na odcinku l = 1 m długości przewodu. Ponieważ siła oddziaływania między przewodami dana jest wzorem
![]()
,
więc podstawiając do tego wzoru wymienione wartości F, L, a oraz I=1A otrzymujemy zarówno wartość liczbową jak również jednostkę stałej konwencjonalnej μ0=4Π*10-7Vs/Am. Drugą stałą ε0 trzeba rzeczywiście doświadczalnie wyznaczyć, gdyż przyjęcie jednostki prądu wyznacza pozostałe jednostki elektryczne, takie jak jednostka ładunku (1C=1A*1s), jednostkę napięcia (z relacji 1V*1A=1W) i jednostkę pojemności (1F=1C/1V) użytą do określenia pojemności naszego kondensatora.
Stwierdzamy zatem, że nawet jeśliby magnetostatyka i elektrostatyka pozostawały niezależnymi zjawiskami fizycznymi wymagają one w próżni tylko jednej stałej doświadczalnej. Pełny układ równań elektromagnetyzmu (równania Maxwella) wiąże wartości ε0 i μ0 z prędkością fali elektromagnetycznej c równaniem
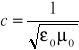
.
Pomiar przenikalności dielektrycznej próżni stanowi więc pośrednią metodę wyznaczania prędkości światła.
Tabela 1. Wartości względnej przenikalności dielektrycznej dla wybranych dielektryków.
MATERIAŁ |
εr |
powietrze |
1,00054 |
polietylen |
2,3 |
polichlorek winylu (PCV) |
2,8 |
pleksiglas |
2,6 |
szkło pyrex |
4,5 |
porcelana elektrotechniczna |
6 - 8 |
krzem |
11,7 |
woda |
80 |
Aparatura.
Do zestawiania kondensatora o różnej geometrii używamy dwu kołowych metalowych okładek, zestawu krążków izolujących (wykonanych z pleskiglasu) i kilku płyt wykonanych z różnych dielektryków. Kondensatorem cylindrycznym jest standardowy kabel koncentryczny. Potrzebne mechaniczne przyrządy pomiarowe to śruba mikrometryczna i przymiar milimetrowy (ewentualnie długa suwmiarka).
Do pomiaru podatności zastosowano cyfrowy miernik MIC-4070D produkcji tajwańskiej. Działa on na zasadzie pomiaru oporności pozornej badanego kondensatora (Xc=1/(2ΠfC)) przy użyciu prądu o częstotliwości 1 kHz. Maksymalny błąd pomiaru C dla wszystkich zakresów miernika wynosi 1% wielkości mierzonej + 0,1% zakresu.
Wykonanie ćwiczenia.
Włączyć miernik LCR do sieci za pośrednictwem miniaturowego zasilacza. Powinien być zaopatrzony w krótkie przewody z „krokodylkami”, na razie nie podłączone do układu. Jeżeli wskazania miernika różnią się istotnie od zera (np. więcej niż 0,3 pF na zakresie 200 pF) wtedy przyrząd należy wyzerować.
Zestawić kondensator z płyt (ustawić dokładnie jedna nad drugą) i trzech pojedynczych izolacyjnych przekładek. Następnie zmierzyć pojemność C i odległość d.
Uwagi:
krążki przekładkowe posiadają jednakową średnicę, natomiast grubości płytek różnią się ze względu na różnice grubości płyty pleskiglasowej, z której zostały wytoczone. Należy mierzyć (śrubą mikrometryczną) indywidualne grubości d1, d2, d3 dla każdego z krążków. Jako wartość d do dalszej analizy brać średnią arytmetyczną.
podczas pomiaru wartości C odsunąć ręce od układu, gdyż dotykanie mierzonego kondensatora powoduje zauważalny wzrost pojemności!
wyniki pomiarów d1, d2, d3 i C oraz obliczone wartości d i Cd notować w odpowiedniej tabeli.
Pomiar pojemności powtórzyć dla wzrastającej liczby 2,3,4,5... przekładek w każdym z trzech słupków krążków (rys.1). Dla każdej konfiguracji mierzyć wysokości każdego słupka. Na zakończenie powtórzyć pomiar dla pojedynczych trzech przekładek.
Zmierzyć pojemności kondensatorów zestawionych z okładek metalowych rozdzielonych płytami wykonanymi z różnych dielektryków.
Zmierzyć pozostałe wymiary potrzebne dla obliczenia ε0 i εr .
Dla odcinka kabla koncentrycznego zmierzyć jego pojemność i niezbędne wymiary geometryczne.
Opracowanie wyników.
Przenikalność dielektryczną próżni.
Wyniki pomiarów d1, d2, d3, i C oraz obliczone wartości dśr i Cdśr pokazuje poniższa tabela:
Wyniki pomiarów: |
d1 [mm] |
d2 [mm] |
d3 [mm] |
Wartość średnia dśr [mm] |
Pojemność C [pF] |
Iloczyn Cdśr [pF*mm] |
Pomiar dla 1 przekładki |
3,26 |
3,29 |
3,12 |
3,223 |
137,40 |
442,886 |
Pomiar dla 2 przekładek |
3,26 |
3,29 |
3,12 |
6,433 |
72,20 |
464,487 |
|
3,22 |
3,23 |
3,18 |
|
|
|
Pomiar dla 3 przekładek |
3,26 |
3,29 |
3,12 |
9,663 |
49,80 |
481,234 |
|
3,22 |
3,23 |
3,18 |
|
|
|
|
3,26 |
3,28 |
3,15 |
|
|
|
Pomiar dla 3 przekładek |
3,26 |
3,29 |
3,12 |
12,470 |
39,70 |
495,059 |
|
3,22 |
3,23 |
3,18 |
|
|
|
|
3,26 |
3,28 |
3,15 |
|
|
|
|
3,08 |
3,09 |
2,25 |
|
|
|
Powtórny pomiar dla 1 przekładki |
3,08 |
3,17 |
3,16 |
3,137 |
140,90 |
441,956 |
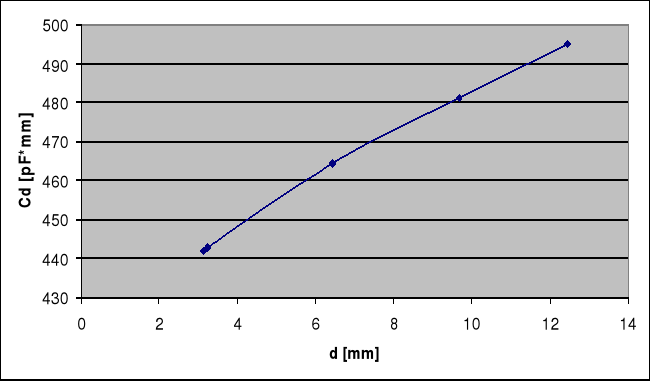
Z wyliczonych danych dśr i Cdśr powstaje wykres zależności iloczynu Cdśr od odległości okładek dśr .
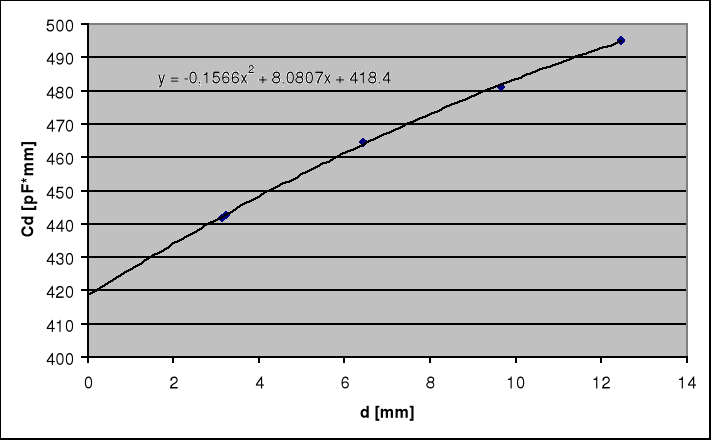
Przez uzyskane punkty wykresu przeprowadzamy gładką krzywą i ekstrapolujemy czyli przedłużamy do wartości dśr = 0. Otrzymujemy poniższy wykres:
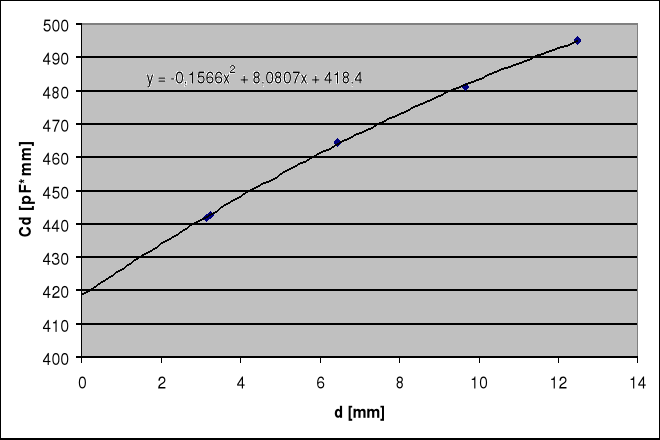
Wykres dany jest wzorem:
Cd = f(d) = -0,1566d2 + 8,0807d + 148,4
z którego wyliczamy wartość dla d = 0 równą:
Cd = f(0) = 418,4 pF*mm = 0,4184 pF*m
Aby policzyć ε0 potrzebne są jeszcze powierzchnie okładek kondensatora i powierzchnie:
okładek kondensatora:
D = 240 mm = 0,24 m - średnica,
S = Π*D2/4 = 0,0452389 m2 - powierzchnia,
pleksiglasowych przekładek:
Zmierzone średnice:
dx1 |
19,97 |
dx2 |
19,96 |
dx3 |
19,94 |
dx4 |
19,97 |
dx5 |
19,98 |
dx6 |
19,93 |
dx7 |
19,96 |
dx8 |
19,96 |
dx9 |
19,94 |
dxśr |
19,96 |
dx = 19,96 mm = 0,01996 m - średnica,
Sp = Π*dx2/4 = 0,000313 m2 - powierzchnia,
Względna przenikalność dielektryczna dla pleksiglasu: ε0r = 2,6
Przenikalność dielektryczną próżni liczymy za wzoru:
![]()
Błąd Δε liczymy z prawa przenoszenia błędów ze wzoru:
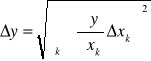
Potrzebne dane:
zakres = 200 pF
εr = 2,6
C = 140,9 pF
d = 0,00314 m
S = Π*D2/4 = 0,0452389 m2
Sp = Π*dx2/4 = 0,000313 m2
ΔC = 1%*C + 0,1%*zakres = 1,609 pF
Δd1 = 0,001 m
Δd = 0,00001 m
ΔS = Π*Δd12/4 = 0,7854*10-6 m2
ΔSp = Π*Δd2/4 = 0,7854*10-10 m2
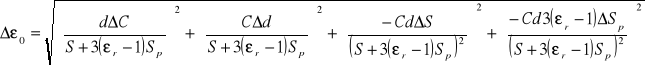
![]()
Zatem przenikalność dielektryczną próżni ε0 = 8,951 ± 0,112 pF/m.
Błąd procentowy wynosi: ![]()
Wartość obliczona ε0 = 8,951 pF/m jest równa wartości tablicowej ε0 = 8,85 pF/m w granicach błędu.
Względna przenikalność dielektryczną dla wybranych dielektryków.
Wyniki pomiarów d i C oraz obliczone wartości εr pokazuje poniższa tabela:
Materiał |
Grubość d[mm] |
Grubość d[m] |
Pojemność C[nF] |
Pojemność C[pF] |
Względna przenikalność dielektryczna εr |
Polichlorek winylu |
3,1 |
0,0031 |
0,402 |
402 |
2,836 |
Ebonit |
3,05 |
0,00305 |
0,763 |
763 |
5,296 |
Pleksiglas |
2,92 |
0,00292 |
0,397 |
397 |
2,638 |
Pleksiglas 2 ? |
3,93 |
0,00393 |
0,314 |
314 |
2,808 |
Uzyskane wyniki porównujemy z wartościami tabelarycznymi:
Materiał |
Obliczone εr |
Tablicowe εr |
Polichlorek winylu |
2,836 |
2,8 |
Ebonit |
5,296 |
5,2 |
Pleksiglas |
2,638 |
2,6 |
Pleksiglas 2 ? |
2,808 |
2,6 |
Z tabeli wynika, że wartości obliczonej względnej przenikalności dielektrycznej są prawie identyczne z wartościami tablicowymi za wyjątkiem dielektryka oznaczonego jako pleksiglas 2 - wynika to stąd, że nie byliśmy w stanie w 100% stwierdzić czy był to rzeczywiście pleksiglas.
Pojemność dla kabla koncentrycznego.
Dane:
2r = 0,68 mm = 0,00068 m - średnica przewodu wewnętrznego,
2R = 4,53 mm = 0,00453 m - średnica izolatora (polietylen),
l = 114 cm = 1,14 m - długość kabla,
C = 77,8 pF - pojemność kabla,
Ze wzoru:
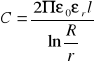
liczymy względną przenikalność dielektryczną polietylenu:
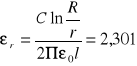
Wartość tabelaryczna wynosi 2,3.
Pomiar prędkości światła.
Dane:
ε0 = 8,951 ± 0,112 pF/m - przenikalność dielektryczna próżni,
μ0 = 1,2566*10-6 Vs/Am - przenikalność magnetyczna próżni,
Prędkość światła liczymy ze wzoru:
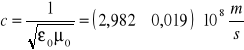
Błąd procentowy prędkości światła równa się 0,63%
Wartość obliczona c = 2,982*108 m/s jest równa wartości tablicowej c = 2,998*108 m/s w granicach błędu.
Porównując względne błędy Δε0 i Δc widać, że błąd względny Δc jest około dwa razy mniejszy.
Wnioski i uwagi.
Wszystkie punkty ćwiczenia zostały wykonane zgodnie z instrukcją prowadzących zajęcia.
Błędy pomiarów są wynikiem niedoskonałości naszych zmysłów oraz klasą używanych przyrządów.
Otrzymana wartość ε0 jest różna od wartości tablicowej o 0,101 pF/m co stanowi 1,14% , a wartość c jest różna od wartości tablicowej o 1,6*106 co stanowi 0,53%.
Ćwiczenie 33 - Przenikalność dielektryczna |
- 1 -
Wyszukiwarka
Podobne podstrony:
13, !Nauka! Studia i nie tylko, Fizyka, Laborki fizyka mostek ćw 32, 32 - Mostek Wheatstone'a, 32-mo
mostek W, !Nauka! Studia i nie tylko, Fizyka, Laborki fizyka mostek ćw 32, 32 - Mostek Wheatstone'a
TS, !Nauka! Studia i nie tylko, Fizyka, Laborki fizyka mostek ćw 32, 32 - Mostek Wheatstone'a
Fizyka 32d, !Nauka! Studia i nie tylko, Fizyka, Laborki fizyka mostek ćw 32, 32 - Mostek Wheatstone'
14, !Nauka! Studia i nie tylko, Fizyka, Laborki fizyka mostek ćw 32, 32 - Mostek Wheatstone'a, 32-mo
Mostek Wheatstone'a, !Nauka! Studia i nie tylko, Fizyka, Laborki fizyka mostek ćw 32
Opracowanie wyników, !Nauka! Studia i nie tylko, Fizyka, Laborki fizyka mostek ćw 32, 32 - Mostek Wh
MOj mostek, !Nauka! Studia i nie tylko, Fizyka, Laborki fizyka mostek ćw 32, 32 - Mostek Wheatstone'
L AB32, !Nauka! Studia i nie tylko, Fizyka, Laborki fizyka mostek ćw 32, 32 - Mostek Wheatstone'a
Fizyka- Sprawdzenie prawa Hooke'a, !Nauka! Studia i nie tylko, Fizyka, Ćwiczenie 11 - moduł Younga
modul younga, !Nauka! Studia i nie tylko, Fizyka, Ćwiczenie 11 - moduł Younga
Fizyka- Sprawdzenie prawa Hooke'a4, !Nauka! Studia i nie tylko, Fizyka, Ćwiczenie 11 - moduł Younga
11.modul younga, !Nauka! Studia i nie tylko, Fizyka, Ćwiczenie 11 - moduł Younga
Paprotnikidod, !Nauka! Studia i nie tylko, Biologia, egzamin biol~, egzamin biol
interaaaaaaaaakcje, !Nauka! Studia i nie tylko, Biologia, kolokwium Biologia!!!
geografia ekonomiczna, !Nauka! Studia i nie tylko, Ochrona środowiska
więcej podobnych podstron