VI. Model wzrostu Solowa

Spis treści:

1. Funkcja produkcji i jej własności

2. Założenia modelu Solowa

3. Równanie Solowa oraz jego interpretacja ekonomiczna

4. Mechanizm dochodzenia do długookresowej równowagi w modelu Solowa

5. Ścieżka zrównoważonego wzrostu

Słowa kluczowe: funkcja produkcji, stałe efekty skali, równanie Solowa, równowaga w modelu Solowa, wzrost zrównoważony

Funkcja produkcji (określana czasami w literaturze - agregatowa funkcja produkcji) opisuje zależność między wielkością produkcji wytwarzanej w gospodarce a nakładami czynników produkcji (Kwiatkowski, Kucharski, Raczko, 2006: 286). Przy założeniu, że zasób wiedzy pozostaje niezmieniony możemy ją zapisać następująco:

(1)

gdzie: Y - wielkość produkcji; K - nakłady kapitału; L - nakłady pracy.

Przyjmujemy, iż w każdym punkcie czasowym gospodarka dysponuje pewnym zasobem kapitału i pracy, które są wykorzystywane w celu wytwarzania produktów. Ponadto przyjmujemy, iż nie da się wytwarzać produktów przy wykorzystaniu tylko jednego z czynników produkcji, to znaczy, że w gospodarce występuje ograniczona substytucyjność czynników produkcji.

Przyjmujemy, że funkcja produkcji opisana równaniem (1) spełnia następujące warunki:

(a)
. (2)

gdzie: MP_K - krańcowy produkt kapitału; MP_L - krańcowy produkt pracy; dY - przyrost produkcji; dK - przyrost nakładów kapitału, dL - przyrost nakładów pracy.

Spełnienie założenia (a) oznacza, że zwiększanie nakładów kapitału lub nakładów pracy prowadzić będzie do zwiększenia produkcji. Krańcowy produkt kapitału to stosunek przyrostu produkcji do przyrostu nakładów kapitału (Kwiatkowski, Kucharski, Raczko, 2006: 286) Krańcowy produkt pracy to stosunek przyrostu produkcji do przyrostu nakładów pracy (Kwiatkowski, Kucharski, Raczko, 2006: 286).

(b)
. (3)

gdzie: dMP_L - przyrost krańcowego produktu pracy; dMP_K - przyrost krańcowego produktu kapitału.

Warunek ten wskazuje, że zwiększanie nakładów jednego czynnika produkcji (przy stałych nakładach drugiego czynnika produkcji) daje coraz mniejszy przyrost produkcji. Spełnienie warunków (a) i (b) oznacza, że funkcja produkcji spełnia prawo malejącej produkcyjności krańcowej względem obu czynników produkcji. Prawo malejących przychodów głosi, iż w miarę wzrostu nakładów jednego czynnika produkcji (przy stałych nakładach drugiego czynnika) produkcja rośnie, ale coraz wolniej, zaś krańcowy produkt tego czynnika maleje.

(c) Funkcja produkcji opisana równaniem (1) charakteryzuje się stałymi efektami skali, czyli ၡ-krotne (ၡ>0) zwiększenie nakładów kapitału i pracy powoduje ၡ-krotny przyrost wielkości produkcji. Funkcja produkcji opisana równaniem (1) jest jednorodna stopnia pierwszego. A zatem, funkcja produkcji spełnia następujące równanie:

(4)

Równanie (4) to tzw. warunek jednorodności funkcji stopnia pierwszego (Kwiatkowski, Kucharski, Raczko, 2006: 287).)

(d) Funkcja produkcji opisana równaniem (1) spełnia warunki Indy, które możemy zapisać w następujący sposób:

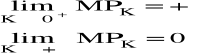
(5a)

oraz:

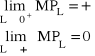
(5b)

To znaczy, że przy bardzo małych nakładach kapitału (pracy) zwiększenie nakładów kapitału (pracy) daje bardzo duży przyrost produkcji (zbieżny do nieskończoności) (Romer, 2000: 28). Przy bardzo dużych nakładach kapitału (pracy) zwiększenie nakładów kapitału (pracy) daje bardzo mały przyrost produkcji (zbieżny do zera) (Romer, 2000: 498).

Ponieważ funkcja produkcji jest jednorodna stopnia pierwszego, to dzieląc obustronnie równanie (1) przez L, otrzymujemy (Kwiatkowski, Kucharski, Raczko, 2006: 287):

(6)

gdzie:
- wydajność pracy;
- techniczne uzbrojenie pracy.

Wydajności pracy to poziom produkcji przypadający na jednego zatrudnionego. Techniczne uzbrojenie pracy to poziom kapitału przypadający na jednego zatrudnionego. Jeśli wydajność pracy oznaczymy literą ỹ, zaś techniczne uzbrojenie pracy literą
, to równanie (6) możemy zapisać następująco:

(7)

Równanie (7) to równanie funkcji wydajności pracy. Funkcja wydajności pracy opisuje zależność między wydajnością pracy a technicznym uzbrojeniem pracy. Wydajność pracy rośnie wraz ze wzrostem technicznego uzbrojenia pracy, ale coraz wolniej. Innymi słowy, funkcja wydajności pracy jest rosnąca i wklęsła względem technicznego uzbrojenia pracy. Ilustrację graficzną równania (7) przedstawiono na rysunku 1.

Rys. 1. Funkcja wydajności pracy

Źródło: Kwiatkowski, Kucharski, Raczko 2006: 288.

Funkcja produkcji spełniająca założenia a-d, w literaturze ekonomicznej określana jest mianem neoklasyczna funkcja produkcji.

Model Solowa w literaturze ekonomicznej jest nazywany neoklasycznym modelem wzrostu, gdyż opiera się on na modelach klasycznych (Hall, Taylor, 2000: 86). Podstawowa wersja modelu Solowa została po raz pierwszy opublikowana w 1956 roku przez Roberta Solowa (Solow, 1956: 65-94) i w dalszym ciągu jest punktem wyjścia każdej analizy wzrostu gospodarczego.

Model Solowa jest modelem długookresowym oraz modelem podażowym. To znaczy, że przyjmuje się w nim założenie, iż gospodarka funkcjonuje przy pełnym wykorzystaniu czynników produkcji. Poziom produkcji w gospodarce Solowa zależy od czynników podażowych, czyli zasobu kapitału, zasobu pracy oraz zasobu wiedzy. Podstawowe założenia modelu Solowa dotyczą właściwości funkcji produkcji oraz zmian w czasie zasobów kapitału, pracy oraz wiedzy. Zasoby: kapitału, siły roboczej, wiedzy oraz strumienie: produkcji, inwestycji oraz oszczędności traktujemy jako wielkości ciągłe w czasie. To znaczy, że wszystkie wymienione wielkości są określone w każdym punkcie czasu. Potraktowanie czasu jako wielkość dyskretną w niczym nie zmienia wniosków płynących z modelu.

W modelu Solowa przyjmujemy następujące założenia (Romer, 2000: 25-30):

1) Proces produkcji w analizowanej gospodarce opisany jest przez funkcję produkcji (spełniającą warunki a-d):

(8)

gdzie: A - zasób wiedzy.

Takie umiejscowienie A w funkcji produkcji oznacza, że w analizowanej gospodarce mamy do czynienia z postępem technicznym zasilającym pracę, czyli z postępem technicznym neutralnym w sensie Harroda (Romer, 2000: 26). Postęp techniczny to dynamiczny proces umożliwiający zwiększenie produkcji przy danych nakładach kapitału i pracy lub osiągnięcie tego samego poziomu produkcji przy niższych nakładach kapitału i pracy.

2) W analizowanej gospodarce jest wytwarzane jedno dobro. Przyjmujemy ponadto, iż gospodarka Solowa jest gospodarką zamkniętą bez udziału państwa. Co oznacza, że produkt wytworzony w tej gospodarce jest dzielony na konsumpcje i inwestycje:

(9)

3) Inwestycje są finansowane z oszczędności (przyjmujemy założenie, że w gospodarce nie ma opóźnień czasowych):

(10)

gdzie: S - oszczędności; I - inwestycje.

4) Funkcja oszczędności jest postaci:

(11)

gdzie: s - stopa oszczędności.

Przyjmujemy, że stopa oszczędności jest stała w czasie. Stopa oszczędności to udział oszczędności w produkcji.

5) Przyrost zasobu kapitału w czasie wynosi:

(12)

gdzie:
- przyrost zasobu kapitału w czasie (jest to pochodna kapitału po czasie -
); I - inwestycje; δ - stopa deprecjacji kapitału; dt - przyrost czasu.

Stopa deprecjacji kapitału to odsetek kapitału, który się zużywa w procesie produkcji. Stopa deprecjacji kapitału taj samo, jak stopa oszczędności jest wielkością egzogeniczną.

6) Stopa wzrostu zatrudnienia w gospodarce wynosi:

(13)

gdzie:
- przyrost zasobu siły roboczej w czasie (jest to pochodna zatrudnienia po czasie -
).

Stopa wzrostu zatrudnienia to stosunek przyrostu zatrudnienia do poziomu zatrudnienia w okresie poprzednim.

7) Stopa postępu technicznego wynosi:

(14)

gdzie:
- przyrost zasobu wiedzy w czasie (jest to pochodna zasobu wiedzy względem czasu -
); m - stopa postępu technicznego.

Stopa postępu technicznego to przyrost zasobu wiedzy do zasobu wiedzy w okresie poprzednim. Postęp techniczny w modelu Solowa ma charakter egzogeniczny, czyli w odróżnieniu od teorii endogenicznego wzrostu nie objaśniamy źródeł postępu technicznego (Hall, Taylor, 2000: 94-95).

Wymieniając wszystkie te założenia zdefiniowaliśmy warunki funkcjonowania gospodarki Solowa. Przejdźmy do analizy funkcjonowania tej gospodarki. Dzieląc obustronnie równanie (12) przez (AL) otrzymujemy:

(15)

Wyrażenie (AL) to nakłady pracy w ujęciu efektywnym (zasilone przez zasób wiedzy). Z założeń 3-4 wynika, że I = S oraz S = sY. Po podstawieniu warunków 3-4 do równania (15) otrzymujemy:

(16)

Przyjmujemy, że:
oraz

gdzie: y - produkcja na jednostkę efektywnej pracy; k - kapitał na jednostkę efektywnej pracy.

A zatem, równanie (16) możemy zapisań w następującej postaci:

(17)

Wiemy, że zasób kapitału na jednostkę efektywnej pracy wynosi:
. A zatem, zasób kapitału wynosi:

(18)

Wszystkie wielkości w równaniu (18) są określone w każdym punkcie czasowym, czyli można wyznaczyć pochodną każdej z tych wielkości względem czasu. Logarytmując obustronnie równanie (18) otrzymujemy:

(19)

Różniczkujemy obustronnie równanie (19) względem czasu (t):

(20)

gdzie:
- stopa postępu technicznego;
- stopa wzrostu zasobu kapitału na jednostkę efektywnej pracy;
- stopa wzrostu zatrudnienia.

Po przekształceniach równanie (20) będzie postaci:

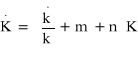
(21)

Po podstawieniu równania (21) do równania (17) otrzymujemy:

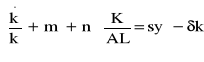
(22)

A stąd, po przekształceniach otrzymujemy najważniejsze równanie w modelu Solowa, czyli równanie Solowa:

(23)

Z równania Solowa wynika, iż przyrost kapitału na jednostkę efektywnej pracy jest równy różnicy między inwestycjami faktycznymi na jednostkę efektywnej pracy a inwestycjami restytucyjnymi na jednostkę efektywnej pracy (Romer, 2000: 31). Wyrażenie (sy) w równaniu (23) to inwestycje faktyczne na jednostkę efektywnej pracy, zaś wyrażenie
to inwestycje restytucyjne na jednostkę efektywnej pracy. Inwestycje restytucyjne są to inwestycje niezbędne do utrzymania zasobu kapitału na jednostkę efektywnej pracy na stałym poziomie. Inwestycje restytucyjne muszą być realizowane z uwagi na deprecjację (zużywanie się) kapitału oraz wzrost nakładów pracy w ujęciu efektywnym.

Ponieważ funkcja produkcji opisana równaniem (8) jest jednorodna stopnia pierwszego, to dzieląc obustronnie równanie (8) przez AL. (Romer, 2000: 27):

(24)

Równanie (24) możemy zapisać w następującej postaci:

(25)

Równanie (25) przedstawia funkcję produktu na jednostkę efektywnej pracy. Opisuje ona zależność między produktem na jednostkę efektywnej pracy a kapitałem na jednostkę efektywnej pracy. Jest rosnąca i wklęsła (tak samo jak omawiana wcześniej funkcja wydajności pracy) względem kapitału na jednostkę efektywnej pracy. Podstawiając równanie (25) do równania (23) równanie Solowa możemy zapisać następująco:

(26)

Z równania (26) wynika, że gdy inwestycje faktyczne są większe od inwestycji restytucyjnych, to z okresu na okres rośnie zasób kapitału na jednostkę efektywnej pracy. W takiej sytuacji w gospodarce mamy do czynienia z niedoinwestowaniem, gdyż inwestycje faktyczne są zbyt niskie dla utrzymania kapitału na jednostkę efektywnej pracy na stałym poziomie. Jeśli natomiast inwestycje faktyczne są mniejsze od inwestycji restytucyjnych, to z okresu na okres zasób kapitału na jednostkę efektywnej pracy będzie malał. W takiej sytuacji w gospodarce mamy do czynienia z przeinwestowaniem, gdyż inwestycje faktyczne są zbyt wysokie dla utrzymania zasobu kapitału na jednostkę efektywnej pracy na stałym poziomie. Gdy inwestycje faktyczne są równe inwestycjom restytucyjnym, to zasób kapitału na jednostkę efektywnej pracy nie zmienia się w czasie, czyli
, zaś gospodarka Solowa znajduje się w stanie długookresowej równowagi.

Rys. 2. Inwestycje faktyczne i inwestycje restytucyjne na jednostkę efektywnej pracy

Źródło: Romer 2000: 32.

Graficzną ilustrację równania (26) przedstawiono na rysunku 2. Linia prosta dodatnio nachylona jest ilustracja graficzną funkcji inwestycji restytucyjnych, natomiast krzywa nachylona dodatnio jest ilustracją graficzną funkcji inwestycji na jednostkę efektywnej pracy, czyli funkcji sf(k). Ponieważ funkcja f(k) jest rosnąca i wklęsła, to funkcja sf(k) jest również rosnąca i wklęsła. A zatem, inwestycje (oszczędności) na jednostkę efektywnej pracy rosną, ale coraz wolniej wraz ze wzrostem kapitału na jednostkę efektywnej pracy. Należy krócic uwagę, iż inwestycje restytucyjne rosną proporcjonalnie względem zasobu kapitału na jednostkę efektywnej pracy, natomiast tempo zmiany inwestycji faktycznych na jednostkę efektywnej pracy zmienia się wraz ze zmianą wartości kapitału na jednostkę efektywnej pracy.

Dla k = 0 inwestycje faktyczne są równe inwestycjom restytucyjnym na jednostkę efektywnej pracy. Nie jest to jednak punkt interesujący z punktu widzenia ekonomicznego. Z warunków Indy wynika, że dla małych wartości kapitału na jednostkę efektywnej pracy krzywa kapitału na jednostkę efektywnej pracy jest bardzo stroma, a zatem krzywa będąca ilustracją inwestycji faktycznych będzie bardzo stroma, co implikuje, że dla małych wartości k inwestycje faktyczne na jednostkę efektywnej pracy będą większe od inwestycji restytucyjnych na jednostkę efektywnej pracy. Z drugiej strony z warunków Indy wynika, iż przy dużych wartościach k, krzywa produktu i tym samym inwestycji faktycznych na jednostkę efektywnej pracy będzie stawała się coraz bardziej płaska. A zatem, przy bardzo dużych wartościach k nachylenie krzywej inwestycji faktycznych będzie mniejsze od nachylenia krzywej inwestycji restytucyjnych, co widać na rysunku 2. Z powyższych rozważań wynika, iż musi istnieć punkt przecięcia krzywych inwestycji faktycznych i inwestycji restytucyjnych przy k>0, czyli punkt E na rysunku 2. W punkcie E gospodarka znajduje się w stanie długookresowej równowagi. Wszystkie punkty na prawo od punktu E charakteryzują się przewagą inwestycji restytucyjnych nad inwestycjami faktycznymi, co oznacza stan przeinwestowania. Wszystkie punkty na lewo od punktu E charakteryzują się przewagą inwestycji faktycznych nad inwestycjami restytucyjnymi na jednostkę efektywnej pracy, co oznacza stan niedoinwestowania.

Z modelu Solowa wynika, iż wzrost gospodarczy ma charakter stabilny, to znaczy z każdego punktu na lewo lub na prawo od punktu E gospodarka będzie samoczynnie zmierzać w kierunku długookresowej równowagi. W sytuacji przeinwestowania, czyli na prawo od punktu E, zasób kapitału na jednostkę efektywnej pracy będzie malał (gdyż inwestycje restytucyjne będą większe od inwestycji faktycznych), co będzie sukcesywnie przybliżać gospodarkę do punktu długookresowej równowagi. W sytuacji niedoinwestowania, czyli na lewo od punktu E, zasób kapitału na jednostkę efektywnej pracy będzie rósł z okresu na okres, co będzie przybliżało gospodarkę do punktu długookresowej równowagi. Należy jednak zwrócić uwagę, iż dochodzenie do długookresowej równowagi nie jest natychmiastowe (Romer, 2000: 40-41).

Współrzędna punktu E, czyli k* to zasób kapitału na jednostkę efektywnej pracy w długookresowej równowadze modelu Solowa. Zasób kapitału na jednostkę efektywnej pracy w długookresowej równowadze Solowa zależy od stopy oszczędności, stopy deprecjacji kapitału, stopy wzrostu zatrudnienia oraz stopy postępu technicznego. Wzrost (spadek) stopy oszczędności powoduje wzrost (spadek) kapitału na jednostkę efektywnej pracy w długookresowej równowadze. Wzrost (spadek) stopy deprecjacji kapitału lub stopy wzrostu zatrudnienia lub stopy postępu technicznego powoduje spadek (wzrost) kapitału na jednostkę efektywnej pracy w długookresowej równowadze Solowa (Romer, 2000: 33-40).

Z równania (25) wynika, iż produkt na jednostkę efektywnej pracy zależy od poziomu kapitału na jednostkę efektywnej pracy, a zatem poziom produktu na jednostkę efektywnej pracy w długookresowej równowadze gospodarki Solowa, który będziemy oznaczać symbolem y*, zależy od poziomu k*, czyli tym samym od tego samego zestawu zmiennych, które wpływają na k*. Możemy powiedzieć, iż produkt na jednostkę efektywnej pracy w długookresowej równowadze modelu Solowa jest rosnącą funkcja stopy oszczędności i malejącą funkcją stopy deprecjacji kapitału, stopy wzrostu zatrudnienia oraz stopy postępu technicznego. Należy podkreślić, iż zmiana wyżej wymienionych wielkości wpływa na poziom y*, nie wpływa natomiast na tempo wzrostu y*.

Jedną z wielkości, na którą ma wpływ polityka państwa jest stopa oszczędności. Państwo może poprzez politykę fiskalną lub pieniężną wpływać na skłonność do oszczędzania. Jednakże siła oddziaływania zmiany stopy oszczędności na poziom produktu na jednostkę efektywnej pracy w długookresowej równowadze jest stosunkowo niewielka. Elastyczności produktu na jednostkę efektywnej pracy w długookresowej równowadze gospodarki Solowa względem stopy oszczędności wynosi (Romer, 2000: 39):

(27)

gdzie:
- udział nakładów kapitału w produkcie.

W przypadku większości krajów udział nakładów kapitału w produkcie wynosi ok. 1/3, a zatem elastyczność y* względem stopy oszczędności wynosi ok. 0,5 (Romer, 2000: 39). To oznacza, że podniesienie stopy oszczędności np. o 5% przyczyni się do wzrostu produktu na jednostkę efektywnej pracy w długookresowej równowadze Solowa o 2,5%.

W punkcie E (na rysunku 2) gospodarka znajduje się na ścieżce zrównoważonego wzrostu. Na ścieżce zrównoważonego wzrostu wszystkie zmienne makroekonomiczne rosną według stałych (niekoniecznie takich samych) stóp wzrostu (Romer, 2000: 33). Tempo wzrostu zatrudnienia i wiedzy jest z założenia stałe. Natomiast stopa wzrostu zasobu kapitału (definiowanej jako przyrost zasobu kapitału w czasie do zasobu kapitału w okresie poprzednim) oraz produkcji na ścieżce zrównoważonego wzrostu jest równa sumie stopy wzrostu zatrudnienia i stopy postępu technicznego. Tempo wzrostu wydajności pracy oraz technicznego uzbrojenia pracy na ścieżce zrównoważonego wzrostu jest równe stopie postępu technicznego. Czyli wzrost gospodarczy w długim okresie jest zależny od stopy postępu technicznego. Tylko poprzez zmianę stopy postępu technicznego możliwe jest przejście gospodarki na wyższą ścieżkę zrównoważonego wzrostu.

Reasumując, z modelu Solowa wynika, iż gospodarka będzie się rozwijała w sposób stabilny. Z każdego punktu będzie samoczynnie zmierzać w kierunku długookresowej równowagi. W krótkim okresie wzrost produkcji zależy od postępu technicznego lub akumulacji kapitału, natomiast w długookresowej równowadze wzrost produkcji jest determinowany jedynie przez postęp techniczny. Rząd może wpływać na wzrost poprzez inwestycje w badania i rozwój, pobudzanie inwestycji oraz zwiększanie bodźców do podejmowania zatrudnienia (Hall, Taylor, 2000: 99-104).

Więcej szczegółowych informacji na temat wzrostu gospodarczego i modelu Slowa znaleźć można w podanej literaturze podstawowej i dodatkowej.

W uproszczeniu możemy przyjąć, że:
.

Musimy pamiętać, iż mamy tu do czynienia z pochodną funkcji złożonej - np. ln(K) - funkcja zewnętrzna to logarytm naturalny, funkcja wewnętrzna - K(t).

Techniczne uzbrojenie pracy

Wydajność pracy

(δ+m+n)k

sf(k)

k

E

k*

Inwestycje na jednostkę efektywnej pracy

---