Rozdział 3.

TRAKCYJNE WYKORZYSTANIE SIŁ PRZYCZEPNOŚCI

3.1. Fizyczne ograniczenia sił napędowych i hamujących pojazdu trakcyjnego [1], [13].

Napędowe siły trakcyjne służą nadaniu pojazdowi wymaganej prędkości oraz pokonywaniu oporów ruchu podczas jazdy z tą prędkością wzdłuż szlaku kolejowego. Siły trakcyjne, zarówno napędowe, jak i hamujące, podlegają ograniczeniu ze względu na zjawisko przyczepności zgodnie z wzorami 1.15-1.16 zilustrowanymi rysunkami 1.7 i 1.8.

Oprócz ograniczenia sił trakcyjnych (od strony fizycznego zjawiska przyczepności) występuje praktyczne ograniczenie tych sił ze względu na skończoną moc silników trakcyjnych.

Wartość siły napędowej F_o(V) [kN] odniesionej do osi zestawów napędnych pojazdu trakcyjnego zależy liniowo od wartości mocy N_ST wywiązywanej w silnikach trakcyjnych:

(3.1a)

gdzie: N_o -moc przekazywana od silników na zestawy napędne pojazdu trakcyjnego [kW];

N_ST - łączna moc silników trakcyjnych pojazdu [KW];

V - prędkość jazdy [m/s];

η_P - sprawność przekładni transmitującej moment napędowy na zestawy kół.

Ograniczenie sił trakcyjnych od strony źródła mocy, zgodnie z wzorem (3.1a), ma inny charakter niż ograniczenie od sił przyczepności.

Rysunek 3.1. Zewnętrzna charakterystyka trakcyjna dla mocy N₁ i N₂;

F_oψ(V) - krzywa przyczepności.

Fizyczne ograniczenie sił trakcyjnych od strony sił przyczepności opisane zostało wzorami 1.15-1.16, w funkcji nacisku Q, zaś ograniczenie sił pociągowych, w funkcji mocy N_o, - wzorem 3.1a.

Ograniczenie sił trakcyjnych siłami przyczepności F_oψ(V) występuje w obszarze prędkości 0<V<V_B, charakterystyki pokazanej na rysunku 3.1a, zaś siłami pociągowymi F_oN(V) w obszarze prędkości V_B<V<V_D.

Należy zauważyć, że wraz ze wzrostem mocy instalowanych na pojazdach trakcyjnych, stosunek sił F_oB/F_oD maleje i zmierza do wartości 1.

Prędkość V_D możemy utożsamiać z konstrukcyjną prędkością maksymalną V_max pojazdu. Stosunek prędkości V_max/V_B = k charakteryzuje zakres możliwości wykorzystania pełnej napędowej mocy pojazdu. Wielkość k nazywamy współczynnikiem rozpiętości prędkości pojazdu trakcyjnego przy pracy z pełną mocą. W zakresie prędkości 0<V<V_B, moc pojazdu nie może być w pełni wykorzystana.

Zewnętrzna charakterystyka trakcyjna stanowi niezbędną ofertową informację techniczno - handlową od strony producenta lokomotyw. W punkcie D charakterystyki pojazd trakcyjny wywiązuje siłę pociągową F_oD, która musi pokonać opór ruchu składu pociągu poruszającego się z prędkością maksymalną.

Ograniczenie sił hamujących (przy elektrodynamicznym hamowaniu pojazdu trakcyjnego), związane z mocą odzyskowego hamowania, ma taki sam charakter jakościowy, jak przy napędzaniu. W odniesieniu do mocy hamowania wzór (3.1a) przybiera nieco inną postać, gdyż kierunek transmisji momentu zmienia się:

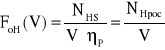
(3.1b)

gdzie: N_HS -moc hamująca silników pojazdu trakcyjnego [kW];

N_Hpoc - łączna moc hamowania pojazdu [KW];

V - prędkość jazdy [m/s];

η_P - sprawność przekładni transmitującej moment hamujący z zestawów kół na silniki pracujące w reżimie generatorowym.

Niska sprawność przekładni sprzyja hamowaniu lecz obniża wydajność napędu.

Oprócz podstawowych, fizycznych ograniczeń sił trakcyjnych w praktyce kolejowej występują czynniki eksploatacyjne, pochodzące od toru, obniżające efektywność trakcyjną kół napędnych (i hamujących) oraz czynniki konstrukcyjne, pochodzące od budowy pojazdu, obniżające efektywność wykorzystania nacisków napędnych (i hamujących) kół na szyny.

3.2. Wpływ nierówności toru na obniżenie efektywności trakcyjnej koła [10]

Pod pojęciem trakcyjnej efektywności koła należy rozumieć praktyczny stopień wykorzystania warunków przyczepności, wynikających z nacisków statycznych, w warunkach dynamiki eksploatacyjnej.

Zaburzenia ruchu obrotowego koła (napędzanego, tocznego lub hamowanego) w pierwszym rzędzie pochodzą od nierówności toru, zwłaszcza w obrębie rozjazdów i krzywych przejściowych, (tzw. rampa torowa przy wejściu w łuk).

Rysunek 3.2. Charakter zaburzeń ruchu koła w obrębie styku szyn. Nierówności toru wydłużają drogę środka koła oraz zakłócają jego prędkość obrotową.

W trakcji kołowej mamy trzy przyczyny zaburzenia ruchu obrotowego:

A - od nierówności toru (nawierzchni);

B - od poślizgów (zaburzeń przyczepności) - zmienność promienia trakcyjnego;

C - od zmienności promienia dynamicznego (ugięcia w strefie kontaktu);

Wymienione przypadki rozważymy kolejno.

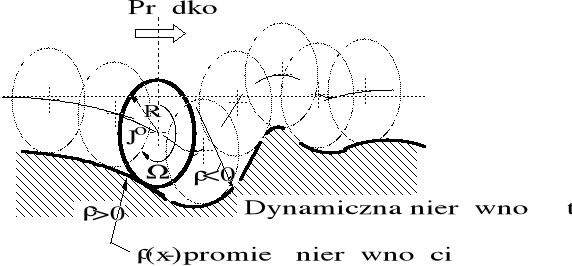
Rysunek 3.3. Ilustracja geometrycznych wymuszeń zaburzenia obrotowego ruchu koła podczas jazdy po nierównościach toru przy ustalonej prędkości ruchu środka koła wzdłuż toru prostego.

Brak zaburzeń - Tor prosty, wyidealizowany:

• prędkość ustalona;

• brak nierówności drogi;

• brak zaburzeń parametrów dynamicznej współpracy koła z nawierzchnią.

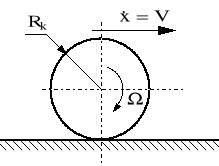
Rysunek 3.4. Wyidealizowany ruch koła po płaskiej nawierzchni.

(3.2)

Ω - Prędkość kątowa koła w warunkach ustalonego ruchu wyidealizowanego

1. Wpływ nierówności drogi.

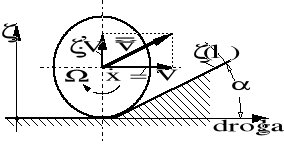
Rysunek 3.5. Przyrost prędkości środka koła przy pokonywaniu nierówności toru.

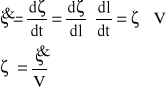
(3.3)

Prędkość wypadkowa

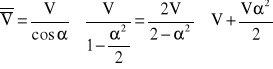
(3.4)

W powyższym przekształceniu wykorzystano rachunek przybliżeń (dostępny w każdym poradniku matematyki); przybliżenie daje błąd 0,1% gdy x<0,031a. Warunek ten jest w eksploatacyjnej praktyce kolejowej spełniony zawsze.

Przyrost prędkości środka koła wynosi:

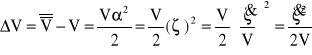
(3.5)

Zaburzenie prędkości kątowej ruchu koła, pochodzące od zarejestrowanych nierówności nawierzchni
, związanych ze zmianą promienia krzywizny nawierzchni (toru) w płaszczyźnie pionowej wynosi:

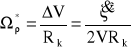
(3.6)

B - Wpływ poślizgów trakcyjnych (quasi-statycznych)

Czyli modelowa zmienność promienia trakcyjnego;

B1 - Przypadek: NAPĘDZANIE V<V₁;

V - prędkość środka koła (rysunek 3.4)

V₁ - prędkość na obwodzie koła.

*) - zgodnie z rachunkiem przybliżeń

Zaburzenie prędkości kątowej koła wyrażone w funkcji poślizgu:

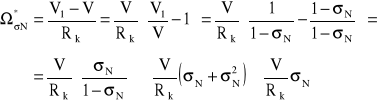
(3.7)

B2 - Przypadek: HAMOWANIE V>V₁;

(3.8)

Ostatecznie, zarówno dla przypadku napędzania jak i hamowania, obowiązuje jednakowy wzór opisujący zależność zaburzenia prędkości ruchu obrotowego koła od poślizgu:

(3.9)

C - Wpływ zmienności promienia dynamicznego

(wpływ dynamicznych ugięć koła i szyny w strefie kontaktu);

(3.10)

W kolejnictwie R_k ≈ const; czynnik „C” jest bardzo mały i na ogół jest pomijany.

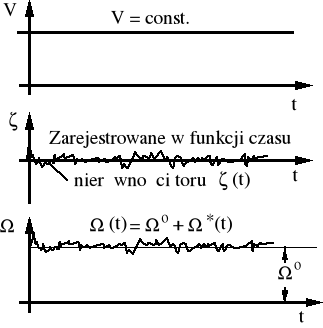
Rysunek 3.6. Zaburzenie obrotowego ruchu koła w funkcji czasu.

Zaburzenie wypadkowe prędkości obrotowej koła,

Uwzględniające wszystkie trzy czynniki zaburzające, otrzymujemy następujący zapis formalny:

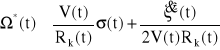
(3.11)

Wypadkowa prędkość obrotowa koła:

(3.12)

Przykład: Ruch koła po torze pofalowanym sinusoidalnie.

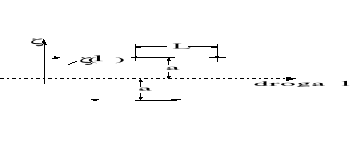
Rysunek 3.7. Ilustracja pofalowania toru (do przykładu).

(3.13)

gdzie ϑ - początkowy kąt obserwacji procesu; przyjmijmy ϑ =0;

Dane do przykładu: R_k = 0,5 [m]; a = 2 [mm]; J_k = 70 [Ns²m];

V=30 [m/s]; L = 2 [m]; Q=5⋅10⁴ [N].

Gdzie J_k - masowy moment bezwładności koła, Q - nacisk koła na tor.

Zgodnie z (3.2), możemy napisać:

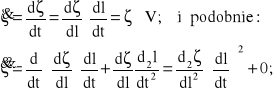
(3.14)

W powyższym wyrażeniu uwzględniono warunek V = const; Zatem:

(3.15)

Bieżący kąt obrotu koła Φ, zgodnie z (11), wynosi:

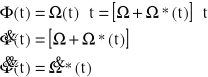
(3.16)

Wyznaczamy kolejno pochodne (3.16) uwzględniając (3.6) i (3.13):

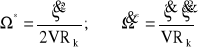
(3.17)

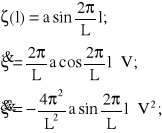
(3.18)

Prędkość zaburzeń ruchu obrotowego koła, poruszającego się po nierówności harmonicznej wynosi więc:

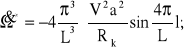
(3.19)

Amplituda momentu harmonicznych przyspieszeń zaburzenia ruchu koła, o momencie masowym bezwładności J_k, wynosi:

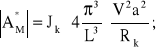
(3.20)

Moment przyczepności koła do szyny wynosi: M_Ψ = Ψ(t)⋅Q⋅R_k;

Przy nacisku koła na szynę wynoszącym Q = 5⋅10⁴ [N], oraz przy wartości współczynnika przyczepności Ψ_(V=30) = 0,2, w wyniku obliczeń porównawczych, otrzymujemy:

Z powyższego widzimy, że harmoniczne pofalowania toru o wysokości zaledwie 2 mm, na długości 2 m, zmniejszają efektywne wykorzystanie przyczepności o około 1,5 promila. Ponieważ „a” występuje we wzorze (3.20) w drugiej potędze, należy postawić pytanie, jaka wartość tego parametru całkowicie wyczerpuje (niweczy) trakcyjną efektywność koła na torze pofalowanym sinusoidalnie.

Proste obliczenie wykazuje, że a_max= 50,6 [mm]. Łatwo jest obliczyć, że przy prędkości 30 [m/s], efektywność trakcyjna spada o 50% gdy amplituda nierówności przekracza 7 [mm]. Taki (porównywalnie) stan toru występuje na wielu liniach.

Konkluzja: Ruch koła po nierównościach toru znacznie obniża efektywność trakcyjną jego napędu i hamowania.

3.3. Wpływ struktury podwozia na obniżenie efektywności trakcyjnej pojazdu. Współczynnik wykorzystania nacisku napędnego [1],[4],[10].

Pod pojęciem napędnego nacisku pojazdu trakcyjnego na tor Q_nL należy rozumieć łączny nacisk napędnych zestawów kół na tor:

(3.21)

gdzie n - liczba zestawów kół napędnych,

Q_nj - nacisk j - tego zestawu napędnego na tor,

Naciski kół zestawów nie-napędnych (tocznych) pojazdu są tu pominięte.

Współczynnik ϑ wykorzystania sił przyczepności dla celów trakcyjnych wyraża stosunek sumy sił pociągowych wywiązywanych na obwodzie wszystkich zestawów napędnych do wartości sił możliwych do wywiązania w warunkach technicznie wyidealizowanych.

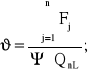
(3.22)

gdzie F_j - siła pociągowa wywiązywana na obwodzie j - tego zestawu napędnego; Ψ = Ψ(V) - współczynnik przyczepności kół do toru.

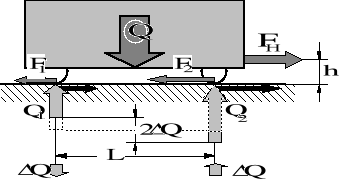
Rysunek 3.8. Płaski schemat trakcyjnie obciążonego pojazdu dwuosiowego jako ilustracja do wyznaczenia współczynnika wykorzystania nacisku zestawów kół napędnych na szyny.

W najprostszym przypadku dwuosiowego pojazdu trakcyjnego z zestawami napędnymi powiązanymi kinematycznie wykorzystanie nacisku napędnego jest pełne. Jeżeli jednak każdy z zestawów jest napędzany indywidualnie przez własny silnik momentem o tej samej wartości to przy niejednakowych naciskach zestawów kół na tor jedynie zestaw o mniejszym nacisku może pracować z jego pełnym wykorzystaniem. W zestawie o nacisku większym część tego nacisku pozostanie nie wykorzystana. Dla pojazdu dwuosiowego, przedstawionego na rysunku 3.8, otrzymujemy:

przy czym:
(3.23)

Ponieważ, jak wyżej napisano, M₁ = M₂, czyli F₁ = F₂, to

Zatem:
(3.24)

Zgodnie z powyższym:

(3.25)

Ponieważ jednak F₁=Q₁⋅Ψ, to po formalnych podstawieniach, otrzymujemy następujący, przemienny szereg potęgowy:

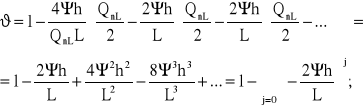
(3.26)

Szereg (3.26) jest zbieżny, gdyż Ψ<1 oraz 2h/L<<1; zatem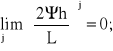

Szereg (3.26) jest zbieżny bezwzględnie, gdyż, dla technicznych wartości Ψ<0,5 oraz 2h/L<<1/4, iloraz sąsiednich wyrazów szeregu, opisany następującym wyrażeniem: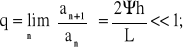
jest stały i mniejszy od jedności. Zgodnie więc z kryterium Leibniza, dla szeregu
wartość bezwzględna jego sumy nie przekracza wartości jego pierwszego wyrazu. Zachowując jedynie dwa wyrazy szeregu (3.26) należy oszacować wartość części odrzuconej szeregu. Wartość ta nie przekracza wartości pierwszego odrzuconego wyrazu. Otrzymujemy więc
; zatem, z dokładnością do ok. 1,5%, dla pojazdu dwuosiowego, możemy przyjąć następujący wzór przybliżony:

(3.27)

Otrzymany wzór (3.27) dotyczy też lokomotyw dwuwózkowych z napędem monosilnikowym.

Istnieje ścisły związek postaci konstrukcyjnej wózka napędnego pojazdu z teoretyczną wartością współczynnika wykorzystania nacisku.

Rozkład trakcyjnych nacisków zestawów kół na szyny

Rozkład nacisków zestawów kół na szyny w silnym stopniu zależy od rozwiązania konstrukcyjnego podwozia pojazdu. Zagadnienie zostanie przykładowo zilustrowane na modelach płaskich.

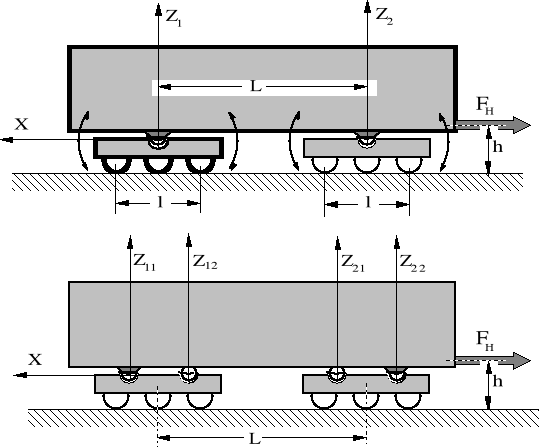
Rysunek 3.9. Schematy oparcia nadwozia na wózku: u góry - oparcie nadwozia w jednej płaszczyźnie poprzecznej - "jednopunktowe"; u dołu - oparcie nadwozia w dwóch płaszczyznach poprzecznych - "dwupunktowe".

Rozróżnia się dwa podstawowe sposoby oparcia nadwozia na wózkach: w jednej płaszczyźnie poprzecznej (w modelu płaskim oparcie jednopunktowe) i w dwóch płaszczyznach („dwupunktowe”). Przedstawiono je na rysunku 3.9. Układ dźwigni wyrównujących naciski wybranych zestawów wózka na tor jest w obydwóch przypadkach odpowiednio dostosowany do sposobu oparcia nadwozia.

Przy oparciu „jednopunktowym” położenie ramy wózka podczas ruchu po nierównościach toru jest określone przez tor; przy oparciu dwupunktowym - przez nadwozie lokomotywy. Przy oparciu jednopunktowym (nadwozia na wózku) naciski zestawów wózka na tor podczas wywiązywania sił trakcyjnych są na ogół zróżnicowane. Przy oparciu dwupunktowym - obowiązkowo wyrównane.

W strukturze wózków występują pary kinematyczne klasy p₅, mające odebrane 5 stopni ruchliwości względnej (tylko możliwość ruchu obrotowego) oraz pary kinematyczne klasy p₄, dające możliwość ruchu obrotowego oraz postępowego. Przykłady pokazano na rysunku 3.10.

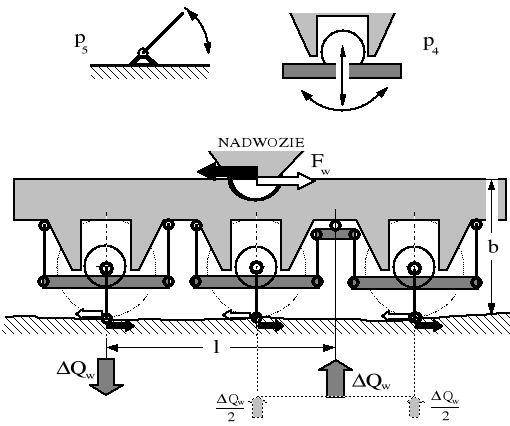
Rysunek 3.10. Moment reakcyjny od sił pociągowych i jego wpływ na wypadkowe naciski statyczne kół wózka trzyosiowego na szyny przy oparciu nadwozia w jednej płaszczyźnie poprzecznej.

Na początek obliczymy ruchliwość ramy wózka z oparciem w jednej płaszczyźnie poprzecznej czyli - w modelu płaskim - „jednopunktowym”. Liczba członów mechanizmu wynosi n = 14. Liczby par kinematycznych wynoszą odpowiednio: p₄ = 3, p₅ = 19. Ruchliwość W ramy wózka względem toru wyznacza się według wzoru:

W = 3n - p₄ - 2p₅ = 42 - 3 − 38 = 1; (3.28)

Na ruchliwość tę składa się jedynie ruch wzdłuż toru. Rama nie ulega swobodnemu galopowaniu względem toru. Jest ona przez tor stabilizowana, zatem oparcie nadwozia może być jednopunktowe. Moment pochodzący od siły F_w, działającej na ramieniu b nie może być zrównoważony od strony nadwozia lecz jedynie od strony toru. W takim przypadku następuje odciążenie 0,5⋅ΔQ_w zestawu pierwszego i drugiego (licząc od lewej do prawej strony rysunku), oraz dociążenie zestawu trzeciego o wielkość ΔQ_w:

(3.29)

W tym przypadku naciski statyczne (przy braku siły pociągowej) mogą być całkowicie wyrównane konstrukcyjnie lecz podczas pracy trakcyjnej różnicują się: Q₁=Q₂, Q₂≠Q₃. Wartości współczynników wykorzystania przyczepności, dla napędu indywidualnego wózków, w obrębie wózka, są następujące:

• dla kierunku ruchu w lewo:
  (3.30a)

• dla kierunku ruchu w prawo:
  (3.30b)

Stopień wykorzystania napędnego nacisku pojazdu trakcyjnego nie zależy od typu (rodzaju, odmiany) części mechanicznej układu napędowego z silnikiem zawieszonym w obrębie wózka. Zależy natomiast od połączeń silników elektrycznych i ich sterowania oraz od układu mechanicznego przeniesienia sił pociągowych z wózka na nadwozie.

Wyznaczymy teraz ruchliwość ramy wózka z oparciem dwupunktowym. Liczba członów mechanizmu wynosi n = 15. Liczby par kinematycznych wynoszą odpowiednio: p₄ = 3, p₅ = 20. Ruchliwość W ramy wózka względem toru wyznacza się według tego samego - co poprzednio - wzoru:

W = 3n − p₄ − 2p₅ = 45 − 3 - 40 = 2; (3.31)

Na ruchliwość tę składa się ruch wzdłuż toru oraz „galopowanie”. Aby rama wózka nie przybierała dowolnych położeń galopujących, jej położenie powinno być stabilizowane przez oparcie dwupunktowe.

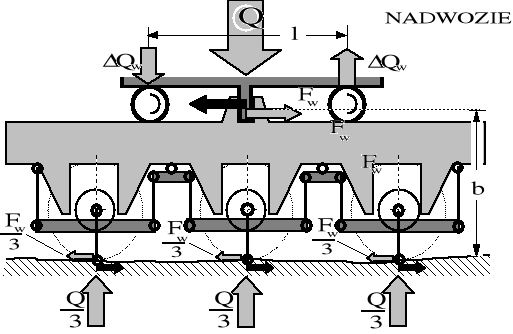
Rysunek 3.11. Rozkład nacisków wózka i moment reakcyjny od sił pociągowych przy oparciu nadwozia na wózku w dwóch płaszczyznach poprzecznych.

Struktura zawieszenia ramy wózka na zestawach zapewnia pełne wyrównanie nacisków wszystkich zestawów wózka na tor. Oznacza to, że w obrębie każdego wózka, niezależnie od sposobu realizacji napędu wózka, (grupowy, indywidualny), mamy pełne wykorzystanie nacisku napędnego. Poszczególne wózki jednak będą wywierać zróżnicowane naciski na tor. W obrębie całej lokomotywy nie ma więc możliwości pełnego wykorzystania nacisku napędnego. W następstwie działania siły F_H, przyłożonej na wysokości h, występuje trakcyjne odciążenie wózka pierwszego i dociążenie drugiego (tylnego) o wielkość ΔQ:

(3.32)

Ponieważ wszystkie zestawy kół omawianego wózka mają wyrównane naciski statyczne, przeto każdy z zestawów wózka ulega odciążeniu (dociążeniu) o wartości Q/3 według wzoru (3.32).

Podsumowując to, co powyżej powiedziano, należy stwierdzić, że naciski statyczne poszczególnych zestawów kół lokomotywy (zarówno ramowej jak i wózkowej) na tor, z woli konstruktora, powinny być wyrównane. Zatem, przy wywiązywaniu siły pociągowej F_H, występują odciążenia przedniego wózka i dociążenia drugiego, zgodnie z (3.31). Jeżeli konstrukcja wózka nie zapewnia samoczynnego wyrównania nacisków jego zestawów przy wywiązywaniu sił trakcyjnych, to wystąpią odciążenia / dociążenia poszczególnych zestawów w obrębie każdego wózka odpowiadające poszczególnemu rozwiązaniu konstrukcyjnemu podwozia jak pokazano na przykładach rys. rys. 3.10 i 3.11.

Wprowadźmy pojęcie współczynnika odciążenia / dociążenia λ_z zestawu w obrębie wózka stosownie do jego konstrukcji. Przykładowo, zgodnie z rysunkiem 3.10, numerując zestawy: lewy - L; środkowy - S; prawy P, możemy napisać:

Ponumerujmy wszystkie zestawy w sześcioosiowej lokomotywie według zasady:

i - numer wózka (licząc od przodu lokomotywy); (i=1,2);

j - numer zestawu w wózku (j= 1,2,3);

n_zl - liczba zestawów w lokomotywie;

n_zw - liczba zestawów w wózku.

Nacisk i,j-tego zestawu lokomotywy wózkowej (numerując zarówno wózki jak i zestawy kolejno od przodu) wyraża się następująco:

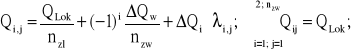
(3.33)

Doskonalenie wykorzystania przyczepności jest zadaniem konstruktora pojazdu.

3.4. Moc pojazdu trakcyjnego w ruchu ustalonym [13].

W ruchu ustalonym (ze stałą prędkością) siła napędzająca pojazdu trakcyjnego równoważy całkowity opór ruchu pociągu. We wzorach podanych w rozdziale 2, obydwie te siły były m.in. wyrażone w odniesieniu do osi zestawów napędnych (czyli rachunkowo bilansowane na poziomie tych osi). Takie ujęcie jest spotykane najczęściej:

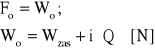
(3.34)

gdzie Q jest wyrażone w [kN], i w [%o], zaś W_zas w [N].

Dla zapewnienia ustalonego ruchu pociągu z zadaną prędkością moc łączna silników trakcyjnych N_ST powinna wynosić:

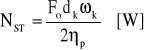
(3.35a)

gdzie: ω_k - prędkość kątowa zestawów kołowych:

d_k - średnica kół napędnych [m],

η_p - sprawność przekładni.

Niekiedy jeszcze można spotkać w dawniejszej literaturze prędkość jazdy wyrażoną tradycyjnie w [km/h]. W takim przypadku wzór (3.35) przybiera następującą postać:

(3.35b)

Ponieważ siła napędzająca Fo=Wo w ruchu ustalonym jest wyrażona w postaci wielomianu (2.36), w którym prędkość jazdy występuje w drugiej potędze, to zgodnie z wyrażeniem (3.35b) widzimy, że zapotrzebowanie na moc silników trakcyjnych pojazdu bardzo silnie wzrasta ze wzrostem prędkości gdyż w zapisie N_ST(V) wystąpi m. in. wyraz zawierający prędkość jazdy V w potędze trzeciej. Wyraz opisujący wzniesienie i[%o] zawiera prędkość w potędze pierwszej. Z powyższego wynika, że wraz ze wzrostem prędkości, wzrost mocy jest skierowany głównie na pokonywanie oporu aerodynamicznego. Przykładowe obliczenia przytaczane w pracy [2] wykazały, że na pokonywanie wzniesienia i=+2[%o] z prędkością V=80[km/h], przez pociąg pasażerski zapotrzebowanie mocy rośnie (w stosunku do ruchu po torze poziomym) o około 50[%]. Natomiast przy prędkości 200 [km/h], już tylko o około 15 [%]. Aby jednak uniknąć zwodniczych porównań wielkości bezwymiarowych należy przy tym dodać, że moc pojazdu, niezbędna do podniesienia prędkości ruchu ustalonego z 80 do 200 [km/h], wzrosła aż niemal 16-krotnie! (15,625 raza).

W zakończeniu niniejszego rozdziału należy zauważyć, że moce pojazdów trakcyjnych, przypadające na pojedynczy zestaw napędny, w nowoczesnych lokomotywach nieustannie rosną dochodząc dość często nawet do 1600 [kW].

Fizyczne zjawisko przyczepności narzuca najsilniejsze ograniczenie temu wzrostowi. Dla ilustracji, na rysunku 3.12, przedstawiono wykres granicznych wartości mocy N_o przypadających na oś pojedynczego zestawu napędnego o nacisku Q=200 [kN] w funkcji prędkości jazdy. Wartości graniczne mocy zależą liniowo od nacisku Q. Jako podstawę wyznaczenia sił przyczepności przyjęto wzór Andrewsa (1.16). Przy budowie wykresu nie uwzględniono żadnych zapasów sił przyczepności.

Rysunek 3.12. Wartości granicznych mocy --> przypadaj[Author:JM] ących na pojedynczy zestaw napędny o nacisku statycznym Q = 200 [kN].

Analiza wykresu wyjaśnia zasadnicze przyczyny tradycyjnego zróżnicowania konstrukcyjnych parametrów towarowych lokomotyw względnie wolnobieżnych i pasażerskich szybkobieżnych oraz zastosowania zespołów trakcyjnych do ekspresowych przewozów pasażerskich. W tym ostatnim zastosowaniu proces hamowania z odzyskiem energii jest równie poważnym czynnikiem określającym budowę pojazdu jak i proces wywiązywania sił pociągowych. Z powodu ograniczeń nacisków kół na tor oraz fizycznych ograniczeń sił przyczepności, wielkie moce (napędowe i hamujące) pojazdów muszą - z konieczności - być „rozdane” pomiędzy znaczną liczbę osi.

66

B

A

D₁

D₂

N₁

N₂

F_o(V)

F_oN(V)

F_oD

F_oB

V_B

V_D

V

F_o

N₂>N₁

L

S

P

400

800

1200

1600

20

40

60

80

100

0

V [m/s]

N_o [kW]

1701

837,56

1226,7

1451,6

1598,1

---