I TD 07.11.2006

Laboratorium z fizyki

Ćw. nr : 14

Wyznaczenie współczynnika tarcia tocznego

Piotr Ptasiński

L3

I. Wstęp teoretyczny

1. Tarcie statyczne i dynamiczne.

2. Ruch obrotowy bryły sztywnej.

3. Ruch harmoniczny tłumiony.

Wprowadzenie.

Zjawisko występowania oporów podczas ruchu ciała stałego nazywamy tarciem. Tarcie pojawia się przy poruszaniu się ciała w cieczy lub gazie i wtedy nazywamy je tarciem wewnętrznym (lepkością), jak również przy kontakcie ciała z powierzchnią innego ciała stałego (tarcie zewnętrzne), a wtedy w zależności od tego, czy ciała przylegają bez ruchu, ślizgają się lub toczą jedne po drugich, mówimy o tarciu przylegania, tarciu przy poślizgu i tarciu przy toczeniu.

Siła tarcia wewnętrznego (oporu lepkiego) jest przeciwnie skierowana do prędkości ruchu ciała i zależy od lepkości cieczy oraz rozmiaru i kształtu ciała oraz od wartości prędkości, do której jest wprost proporcjonalna:

, (1)

gdzie b jest współczynnikiem oporu lepkiego, zależnym od lepkości cieczy oraz rozmiaru i kształtu ciała.

Tarcie zewnętrzne polega na powstawaniu oporu w płaszczyźnie zetknięcia, podczas ruchu względnego dwóch stykających się ciał.

Wyróżniamy siłę tarcia przy poślizgu, występującą podczas ruchu względnego dwóch stykających się powierzchni, która jest proporcjonalna do nacisku ciała na podłoże N.

(2a)

oraz siłę oporu przylegania, czyli siłę tarcia statycznego, występującą, gdy nie ma ruchu względnego dwóch stykających się powierzchni, której wartość wynika z warunków ruchu ciała (I lub II zasada dynamiki), ale która nie może przekroczyć wartości granicznej T_gr

gdzie
(2b)

gdzie: f_k - kinetyczny współczynnik tarcia (bezwymiarowy),

f_s - statyczny współczynnik tarcia (bezwymiarowy).

Z doświadczenia wiadomo, że f_k > f_s. Współczynniki tarcia w pierwszym przybliżeniu nie zależą od siły nacisku na podłoże, ale zależą od rodzaju powierzchni stykających się (gładkość powierzchni, temperatura, wilgotność, zanieczyszczenia). Z zależności (2a) i (2b) widać, Ŝe obie siły tarcia zewnętrznego nie zależą od wielkości stykających się powierzchni, a siła tarcia przy poślizgu nie zależy od prędkości poślizgu (takie tarcie nazywamy tarciem suchym).

Podczas toczenia się ciał występuje tarcie toczne. Toczenie jest złożeniem ruchu postępowego i obrotowego. W dynamice ruchu obrotowego wielkościami analogicznymi do sił są momenty sił. Dlatego analogiem siły tarcia jest tutaj moment siły tarcia M_t. Tarcie toczne można scharakteryzować poprzez współczynnik tarcia tocznego f_t:

(3)

gdzie: M_t - moment siły tarcia,

f_t - współczynnik tarcia tocznego (mający wymiar metra),

N - siła nacisku ciała na podłoże (obciążenie normalne).

Wartość współczynnika tarcia tocznego zależy od rodzaju materiałów, chropowatości powierzchni, temperatury.

Na wstępie rozpatrzmy toczącą się po płaszczyźnie poziomej kulę o masie m i promieniu r, na którą działa zewnętrzna pozioma siła F (rys.1).

Rys. 1. Siły i momenty sił działaj

Z warunku równowagi sił w pionie wynika, że pionowa siła reakcji podłoża F_R jest równa sile ciężkości
. Z równania (3) otrzymujemy wartość momentu tarcia tocznego
. Siła F, jeżeli jest wystarczająco duża, zapewnia ruch przyśpieszony środka masy kuli oraz przyśpieszony ruch obrotowy kuli. Ze wszystkich sił tylko siła F daje niezerowy moment względem punktu styku z podłożem i dlatego przyśpieszenie kątowe wyznaczone dzięki II zasadzie dynamiki dla ruchu obrotowego jest równe:

gdzie J jest momentem bezwładności kuli.

Na ruch postępowy środka masy kuli, oprócz siły F, wpływa także pozioma siła reakcji podłoża T_s (siła tarcia statycznego). Dlatego II zasada dynamiki dla ruchu postępowego ma postać

Jeżeli założymy, że nie występuje poślizg (T_s< T_g = f_sN), to ruch postępowy musi być „dopasowany” do ruchu obrotowego w tym sensie, że obowiązuje zależność między przyśpieszeniem liniowym i kątowym

a=εr

Dopasowanie to jest możliwe dzięki odpowiedniej wartości siły tarcia statycznego T_s.

Zestawiając powyższe równania

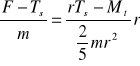
można wyznaczyć wartość siły tarcia statycznego:

(4)

Siła wypadkowa działająca na kulę jest zatem równa:

(5)

Otrzymane wyrażenie na siłę wypadkową jest praktyczne, tzn. po podzieleniu przez masę można bezpośrednio obliczyć przyśpieszenie środka kuli.

Rys. 2. Schemat pomiarowy do wyznaczania współczynnika tarcia tocznego

Układ pomiarowy przedstawiony jest na rys. 2. Zasadniczym elementem przyrządu jest wahadło nachylne składające się z nici, do której zamocowana jest kulka z wodzikiem (9) oraz wspornik (5), gdzie po prowadnicach wsuwa się badaną próbkę (10), czyli metalową płytkę, po której toczy się kulka. Pokrętło (11) służy do pochylenia kolumny (8) wahadła wraz z płytką (10), w celu wykonywania zasadniczych pomiarów współczynnika tarcia tocznego. W czasie drgań wahadła następuje proces mierzenia czasu po przyciśnięciu przełącznika W2. Proces liczenia trwa do momentu przyciśnięcia przełącznika W3. W czasie pomiaru przyrząd musi być dokładnie wypoziomowany przy pomocy nóżek o regulowanej wysokości. Do pomiaru średnicy kulki użyć suwmiarki lub śruby mikrometrycznej.

Wyprowadźmy wzór, z którego będziemy mogli wyznaczyć współczynnik tarcia tocznego. W tym celu skorzystamy z zastosowanego w ćwiczeniu wahadła nachylnego (kulki z wodzikiem 9) o ciężarze Q, które pochylone jest pod kątem β względem pionu (rys. 3a). Na podstawie rozkładu sił otrzymamy składową ciężaru wahadła wzdłuż kierunku największego spadku na płaszczyźnie próbki Q_s i składową prostopadłą do tej płaszczyzny Q_w:

(6)

(7)

Rys. 3. Rozkład siły ciężkości działającej na kulkę wahadła znajdującą się na pochylonej płaszczyźnie

Po odchyleniu wahadła (kulki 9) od położenia równowagi o kąt o a (rys. 3b) kulka zaczyna toczyć się po badanej próbce (10) pod wpływem składowej siły Q_s2. Zgodnie z rozkładem sił otrzymamy wyrażenie na tę składową, słuszne dla dowolnego kąta α:

dla małych kątów sinα≈α, otrzymamy zatem zależność przybliżoną:

(8)

Ze względu na to przybliżenie należy dążyć do tego, aby amplituda wahań o a nie przekraczała paru stopni.

Rozpatrzmy ruch obrotowy wahadła względem punktu zawieszenia. Wszystkie wyznaczane poniżej momenty sił będziemy liczyć względem tego punktu.

Składowa Q_w jest równoważona przez siłę reakcji podłoża, składowa Q_s1 nie daje momentu siły względem punktu zawieszenia, widać więc, że składowa Q_s2 pełni rolę siły zewnętrznej z rozpatrywanego wcześniej wstępnego przykładu z toczącą się kulą. Gdyby tarcie toczne nie występowało ( 0 = t M ), to po uwzględnieniu siły tarcia statycznego, moglibyśmy wyznaczyć wypadkową dwóch sił Q_s2 i T_s, korzystając ze wzorów (5) i (8):

a na tej podstawie - moment tej siły wypadkowej względem punktu zawieszenia

(9)

zależny od kąta wychylenia a i odpowiedzialny za ruch drgający wahadła nachylnego. Przez porównanie z przypadkiem zwykłego wahadła matematycznego, gdzie analogiczny moment siły jest równy a M=-RQα, a jego okres -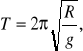
można napisać wzór na okres wahadła nachylnego:

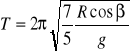
(10)

Współczynnik
stojący w powyższym wzorze jest odbiciem faktu, że kulka toczona pod wpływem jakiejś siły będzie miała mniejsze przyśpieszenie, niż nie obracające się ciało o tej samej masie.

Dodajmy teraz do rozważań ruchu kulki tarcie toczne. Ze wzoru (5) widać, że siła wypadkowa działająca na kulkę zmniejszy się o wartość
, (bo o tyle zwiększy się siła tarcia statycznego, przeciwstawiająca się ruchowi). Wartość tę można traktować jako siłę hamującą, skierowaną przeciwnie do kierunku ruchu wahadła, wynikającą z istnienia momentu tarcia tocznego M_t. Moment tej siły względem punktu zawieszenia jest równy:

a po podstawieniu siły Q_w, danej wzorem (7), za siłę nacisku N, otrzymujemy:

(11)

Ten stały, co do wartości hamujący moment siły, skierowany jest przeciwnie do kierunku obrotu względem punktu zawieszenia. Podczas ruchu wahadła w lewo moment hamujący jest skierowany w prawo i dlatego spowoduje on przesunięcie położenia równowagi wahadła w prawo o kąt ε, co wynika z wykresu na rys. 4. Na wykresie tym, przedstawiającym zależność momentów sił od kąta obrotu, momenty sił kierujące kulkę w prawo są dodatnie. Widać, że dopóki kulka nie zmienia kierunku, jej ruch podlega tym samym prawom, co zwykły ruch drgający (bez tarcia), pod wpływem wypadkowego momentu siły M_w proporcjonalnego do wychylenia α-ε z położenia równowagi α=ε (rys. 4).

Rys. 4. Wychylenie w lewo: a)momenty sił działające na wahadło, b) schemat ruchu

Przesunięcie kątowe położenia równowagi wahadła można obliczyć z warunku równowagi momentów żądając, aby w tym położeniu moment wypadkowy był równy zeru

z czego dostajemy kąt równowagi:

(12)

Na rys. 4 przedstawiono ruch wahadła w lewo, po wychyleniu w prawo o kąt α₀ od linii największego spadku na pochyłej płytce (linia ta widoczna jest na rysunku jako linia pionowa). Widać, że ruch jest symetryczny wokół chwilowego położenia równowagi α=ε, a amplituda jest równa α₀=εα. Powoduje to jednak, że największe wychylenie kulki w lewo, licząc od linii największego spadku, będzie równe α₀-2ε. Po osiągnięciu tego największego wychylenia kulka zaczyna poruszać się w prawo, a wtedy moment hamujący M_h, wynikły z tarcia tocznego, szybko zmienia kierunek, co powoduje ustalenie się nowego położenia równowagi α=-ε. Dlatego ruch w prawo jest analogiczny do poprzedniej fazy ruchu, a największe wychylenie w prawo, licząc od linii największego spadku, zmniejsza się znów o kąt 2ε, co daje łączną zmianę o kąt 4ε, w porównaniu z początkowym wychyleniem α₀-α₁=4ε.

Dalej ruch przebiega podobnie i dla n-tego maksymalnego wychylenia zachodzi:

(13)

Wyznaczając z tej zależności ε i podstawiając do równania (12), dostajemy wzór, dzięki któremu można obliczyć współczynnik tarcia tocznego

(14)

gdzie: r - promień kulki w milimetrach,

α₀ - kąt początkowego wychylenia wahadła [rad],

α_n - kąt odczytany po n „okresach” drgań wahadła [rad],

n - liczba pełnych wahnięć,

β - kąt nachylenia wahadła odczytany na skali bocznej.

Z przedstawionych powyżej praw, jakim podlega ruch wahadła nachylnego z uwzględnieniem tarcia tocznego, wynika też, że skoro poszczególne wahnięcia można traktować jako swobodne, to znaczy bez tarcia tocznego, ale za to z przemieniającym się cyklicznie położeniem równowagi α=±ε, to okres drgań wahadła nie zależy od wielkości tarcia tocznego. Na skutek zmian położenia równowagi zmienia się tylko amplituda wychyleń, a okres wahadła swobodnego nie zależy od amplitudy (dla niewielkich wychyleń).

Warto zauważyć, że wszystkie powyższe rozważania nie uwzględniają ruchu precesyjnego kuli, spowodowanego zmianą kierunku osi obrotu kuli w trakcie ruchu wahadła. Zmiany tego kierunku będą tym mniejsze, im mniejsza będzie amplituda wahań. Dlatego należy tym bardziej dążyć do tego, aby amplituda ta nie przekraczała paru stopni.

2. Wykonanie ćwiczenia

Do wykonania ćwiczenia została użyta kulka z niklu, oraz układ pomiarowy do wyznaczania współczynnika tarcia tocznego składający się z wahadła, którego nachylenie mogło być regulowane. W skład układu pomiarowego wchodziło jeszcze liczydło okresów oraz czasomierz.

3. Tabela pomiarowa

2R		n	0	n	t	T	ft	ft ±∆ ft
[mm]	[^o]	[]	[rad]	[rad]	[s]	[Hz]	[mm]	[mm]
20	15	5	0,105	0,044	8,041	1,61	2,89	2,89 0,014
										0,042	8,037	1,61
										0,042	8,025	1,61
										0,045	8,052	1,61
										0,044	8,029	1,61
						5			0,105	0,042	8,027	1,61
										0,040	8,011	1,60
										0,042	8,024	1,60
										0,044	8,001	1,60
										0,044	7,98	1,60
					30	5			0,105	0,040	8,329	1,67	1,49	1,49 0,008
										0,035	8,321	1,66
										0,037	8,27	1,65
										0,038	8,19	1,64
										0,035	8,277	1,66
						5			0,105	0,037	8,247	1,65
										0,033	8,291	1,66
										0,035	8,251	1,65
										0,035	8,251	1,65
										0,037	8,285	1,66

4. Obliczenia z komentarzem i analiza niepewności

Prezentuje przykładowe obliczenia, pozostałych dokonałem w programie Microsoft Office

1.Obliczam okres wahadła nachylonego pod kątem 15^O

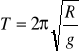
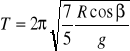
Za R przyjmujemy sumę długości nici (L) i promienia badanej kulki (r).

L = 0,46 [m]

r = 0,01 [m]

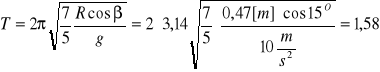
[Hz]

2. Obliczam okres wahadła nachylonego pod kątem 30^O

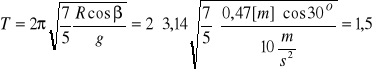
[Hz]

3.Obliczam wartość okresu T z zależności
dla badanej próbki.

[Hz]

4. Obliczam współczynnik tarcia tocznego dla badanej próbki.

[mm]

[mm]

[mm]

5. Wyznaczam niepewność odczytu na skali wahadła.

6. Niepewność
wyznaczam za pomocą różniczki zupełniej dla

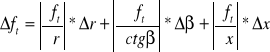
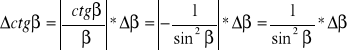
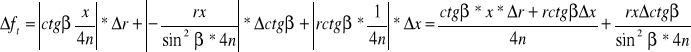
[rad]

[rad]

Błąd względny procentowy dla niklu to

Prezentuje jedynie przykładowe obliczenia, pozostałych dokonałem w programie Microsoft Excel.

5. Wnioski

Współczynnik tarcia wynosi dla niklu: 1,55±0,095[mm]. Na wielkość siły tarcia tocznego wpływa długość promienia kulki, nie ma ona znaczenia gdy chodzi o okres drgań wahadła. Im cosβ kąta nachylenia wahadła jest większy tym krótszy jest okres wahadła i mniejsza siła tarcia tocznego. W tarciu suchym ( niezależnym od prędkości) okres jest wielkością stałą. W tarciu lepkim siła tarcia lepkiego jest proporcjonalna do prędkości ruchu ciał, jeżeli siła tarcia jest tak duża, że współczynnik tłumienia β jest większy od ω_o- częstości drgań nietłumionych układu, tłumienie jest tak silne, że nie obserwujemy drgań układu a więc i okresu.

---