[Politechnika Lubelska		Laboratorium Elektrotechniki
w Lublinie		Ćwiczenie nr 3
Nazwisko ZDERKIEWICZ WÓJTOWICZ ŻUKOWSKI	Imię PIOTR PRZEMYSŁAW PAWEŁ	Grupa: ED.2.5	Rok akademicki 1999/2000
Temat ćwiczenia: Obwody prądu stałego		Data wykonania:9,03,2000	Ocena:

CEL ĆWICZENIA:

Celem ćwiczenia jest poznanie i sprawdzenie podstawowych praw, zasad i twierdzeń

Dotyczących rezystancji prądów i napięć oraz właściwości liniowych obwodów

Elektrycznych prądu stałego.

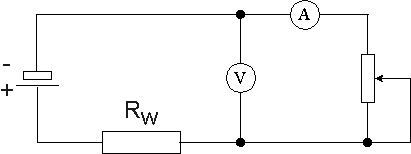
1.Badanie źródeł napięcia.

1. schemat obwodu

2. tabela pomiarowa

Pomiary			Obliczenia
Lp.	U	I	R2	RW	E	P2	P1	=P2/P1
		[V]	[A]			[V]	[W]	[W]	[-]
1.	2,7	0,059	45,7	3,9	2,9	0,16	0,17	0,942
2.	2,65	0,067	39,5	3,9	2,9	0,18	0,195	0,925
3.	2,6	0,078	33,3	3,9	2,9	0,2	0,22	0,909
4.	2,5	0,1	25	3,9	2,9	0,25	0,29	0,862
5.	2,4	0,12	20	3,9	2,9	0,29	0,34	0,852
6.	2,3	0,14	16,4	3,9	2,9	0,32	0,40	0,80
7.	2,1	0,18	11,6	3,9	2,9	0,38	0,52	0,73
8.	1,7	0,26	6,5	3,9	2,9	0,44	0,75	0,586
9.	1,45	0,37	3,9	3,9	2,9	0,54	1,07	0,50
10.	0,14	0,59	0,2	3,9	2,9	0,08	1,71	0,046

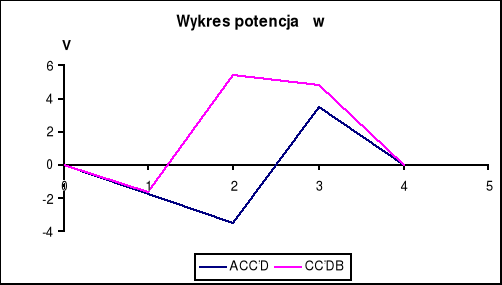
2.Sprawdzanie II prawa Kirchhoffa

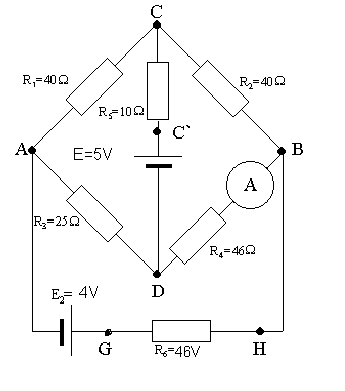
1. schemat obwodu

2. tabela pomiarowa

Obwód	Napięcie na elementach				Suma napięć
	V	V	V	V	V
ACC'D	Uca=1,9	Ucc'=1,6	E1=Uc'd=7	Uad=3,4	0,1
CC'DB	Ucb=4,7	Uc'c=1,6	Uc'd=E1=7	Ubd=0,55	0,15

3. Zasada superpozycji.

Lp.	I	I'	I”	I'+I”
------	[mA]	[mA]	[mA]	[mA]
1	12,5	52	-40	12

4. Sprawdzanie twierdzenia Thevenina

.

I	UBD	RBD	UOBD	IZ	R	R'	IOBL	IOBL'
[mA]	[V]	[Ω]	[V]	[mA]	[Ω]	[Ω]	[mA]	[mA]
12	0,55	46	0,85	32	26,56	29	12,4	11,3

5. Zasada wzajemności

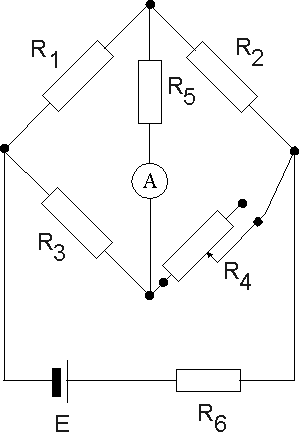
a) schemat obwodu

3. tabela pomiarowa

I'5	I”5	I'6	I”6
[mA]	[mA]	[mA]	[mA]
0	6,2	0	5,8

SPRZĘT POMIAROWY

Woltomierz magnetoelektryczny kl.0,5 nr.3404205,76

Amperomierz magnetoelektryczny kl.0,5 nr.3308045,76

Mostek typ E317A

Zasilacz E1/6 64/3989

Źródło napięcia E=2,9V

Rezystancja R_w=3,9Ω I_N=1,4A

Opornik suwakowy R₂=46Ω , I_N=1,25A

PRZYKŁADOWE OBLICZENIA

Obliczenia(źródła napięcia)

R₂=U/I=2,7/0,059=45,7Ω

E=R_wI+U=3,9*0,059+2,7=2,9V

P₂=U*I=2,7*0,059=0,16W

P₁=E*I=2,9*0,059=0,17W

η=P₂/P₁=0,16/0,17=0,942

P_{2 max}=E²/4R_w=8,41/15,6=0,54W

Obliczenia do zasady superpozycji

I=I'+I''=52-40=12m A

Obliczenia do drugiego prawa Kirchhoffa

E1=UAD+UCC'+UCA=0

Obliczenia do Tw. TEWENINA

R=U_OBD/I_Z=0,85/0,032=26,56Ω

U_obl=I_Z*R'=0,032*29=0,9V

I_obl=U_obl/R_BD+R'=0,9/46+26,56=12,4mA

I'_obl=U_OBD/R_BD+R'=0,85/46+29=11,3mA

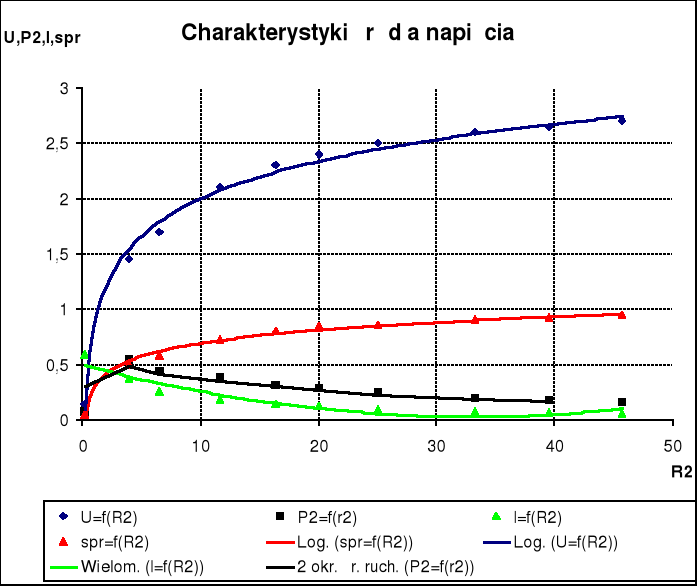
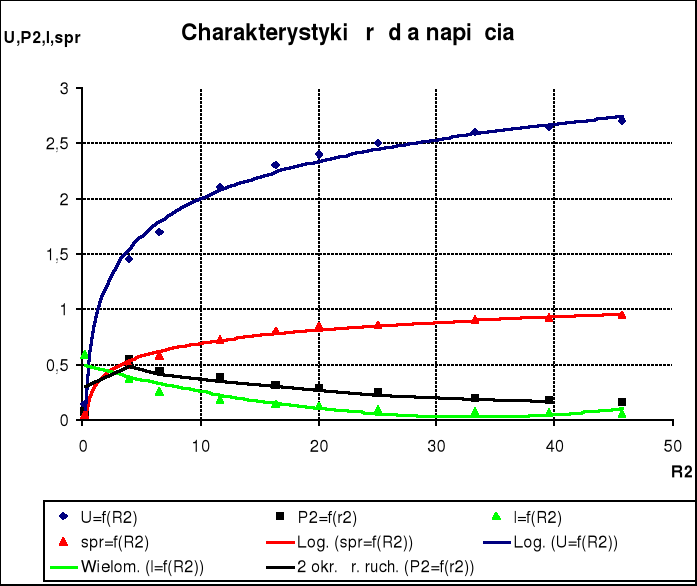
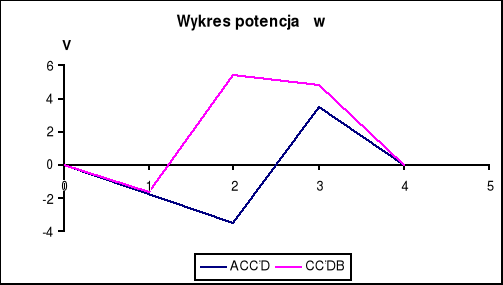
WYKRESY

Wnioski:

Badając źródło napięcia potwierdziły się założenia teoretyczne, iż maksymalna

moc na odbiorniku wydziela się wtedy gdy wartość obciążenia źródła jest równa wartości rezystancji wewnętrznej badanego źródła. Wówczas sprawność obwodu wynosiła 0.5.

Z przeprowadzonych obliczeń wynika ,że moc P₂ ma największą wartość gdy R_w=R₂

i wynosi E²/4R_W.

Wzrost prądu pobieranego ze źródła nie powoduje zmiany E źródła gdyż E nie zależy od R₂ .

Podczas sprawdzania drugiego prawa Kirchhoffa sumy spadków napięć na poszczególnych elementach były bliskie zeru. Różnice te wynikają z niedokładności pomiarów. Otrzymane przez nas wyniki potwierdzają słuszność drugiego prawa Kirchhoffa.

Sprawdzając słuszność zasady superpozycji zauważyliśmy, iż prąd płynący w dowolnej gałęzi obwodu zawierającego więcej niż jedno źródło jest sumą prądów jakie płynęłyby w tej gałęzi dla każdego ze źródeł osobno. Tak brzmi zasada superpozycji.

Twierdzenie Thevenina brzmi : dowolny aktywny obwód liniowy można od strony wybranych zacisków zastąpić obwodem równoważnym złożonym z szeregowo połączonego jednego źródła napięcia równego napięciu pomiędzy zaciskami w stanie jałowym oraz jednej rezystancji równej rezystancji zastępczej obwodu pasywnego, widzianego od strony wybranych zacisków.

Obliczone przez nas wartości metodą Thevenina są w przybliżeniu zgodne z wartościami zmierzonymi. Różnice wynikały z błędów pomiarowych i małej klasy dokładności mierników.

Na podstawie otrzymanych wyników możemy sformułować zasadę wzajemności która brzmi: siła elektromotoryczna działająca w gałęzi n obwodu odwracalnego wywołuje prąd I w gałęzi m to ta siła elektromotoryczna przeniesiona do gałęzi m wywoła taki sam prąd jak w gałęzi n.

---