1. Cel ćwiczenia.

Celem ćwiczenia było bliższe zapoznanie się z procesem zasysania wody oraz określenie charakterystyki pompy próżniowej Q_p = f(∆p) i charakterystyki nieszczelności Q_n = f(∆p), teoretycznego czasu ssania i rzeczywistego czasu ssania na podstawie zarejestrowanych nieustalonych przebiegów zmian ciśnienia w rozpatrywanym układzie. Wykonać zassanie wody ze zbiornika przy układzie szczelnym, układzie z małą nieszczelnością oraz średnią nieszczelnością .

2. Stanowisko pomiarowe.

Pomiary polegały na zasysaniu powietrza do zbiornika pomiarowego przez pompę próżniową przy pełnej szczelności układu oraz stosując w badanym układzie nieszczelności (symulowane przez specjalny zawór), Nieszczelności uzyskujemy stosując wkładki z metalu z wydrążonym otworem (małym, średnim, dużym). Przy pomocy zainstalowanego czujnika wielkość podciśnienia zostaje przeliczona przy pomocy impulsu na miernik, a z miernika na rejestrator. Rejestratorem jest program komputerowy GENIE 3.0. Otrzymane w programie MS EXEL wykresy przedstawiają wykres ciśnienia w zbiorniku w funkcji czasu ∆p = f(t) . Są one podstawą do dalszych obliczeń, których rezultatem będzie poszukiwana charakterystyka pompy próżniowej i nieszczelności.

Stanowisko pomiarowe jest również wzbogacone w rtęciowy manometr różnicowy, na którym dokonujemy dodatkowego odczytu podciśnienia w rurze ssawnej .

S c h e m a t s t a n o w i s k a p o m i a r o w e g o

3. Wyniki pomiarów.

W ćwiczeniu wykonaliśmy trzy próby:

1/ przy pełnej szczelności układu,

2/ przy średniej nieszczelności,

3/ przy małej nieszczelności.

Przykładowe obliczenia.

1/ Dla układu szczelnego

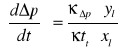
x₁ = x₂ = x₃ = x₅ = x₆ = 20 mm x₇ = 50 mm

y₁ = 60 mm y₂ = 23 mm y₃ = 16 mm

y₄ = 11 mm y₅ = 6 mm y₆ = 2,5 mm y₇ = 2,5 mm

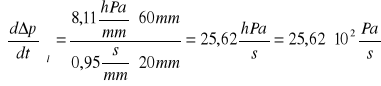
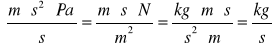
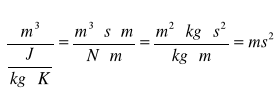
gdzie:

R = 287 J/kg K

T = 293 K

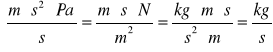
D l a u k ł a d u s z c z e l n e g o
L.p.
1.	300	25,62
2.	600	9,82
3.	71,3	6,83
4.	800	4,7
5.	856,8	2,56
6.	912	1,07
7.	932,4	0,43

3/ Przy średniej nieszczelności

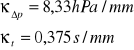
x₁ = x₂ = x₃ = 20 mm x₄ = 12 mm

y₁ = 17 mm y₂ = 12,5 mm y₃ = 6,5 mm y₄ = 1,5 mm

Średnia n i e s z c z e l n o ś ć
L.p.	∆p [hPa]	[hPa/s]	Qn[kg/s]
1.	500	18,9
2.	154	34,7
3.	41,6	18,59
4.	16,7	6,2

4/ Przy małej nieszczelności

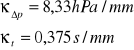
x₁ = x₂ = x₃ = 20 mm x₄ = 12 mm

y₁ = 17 mm y₂ = 12,5 mm y₃ = 6,5 mm y₄ = 1,5 mm

D u ż a n i e s z c z e l n o ś ć
L.p.	∆p [hPa]	[hPa/s]	Qn[kg/s]
1.	500	18,9
2.	154	34,7
3.	41,6	18,59
4.	16,7	6,2

4. Wykresy ∆p = f(t) - Załączniki.

5. Wnioski.

Na podstawie pomiarów wzorcowych układu otrzymaliśmy wykresy wzrostu i spadku podciśnienia w czasie. Przy hermetycznie zamkniętym układzie największa wartość podciśnienia wynosi 940 hPa.

Analizując otrzymane wykresy ∆p = f(t) zauważamy, że:

1. Wzrost nieszczelności powoduje spadek wartości uzyskanego podciśnienia,

- mała nieszczelność po 50 s ∆p = 738 hPa

- średnia nieszczelność po 50 s ∆p ≈ 100 hPa

- duża nieszczelność po 50 s ∆p ≈ 0 hPa

2. Im większa nieszczelność układu, tym mniejsza wysokość ssania pompy. Pomijając straty liniowe oraz miejscowe teoretyczna wysokość ssania
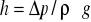
   po 50 s jest odpowiednio dla :

- całkowitej szczelności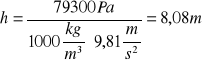

- małej nieszczelności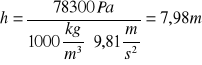

- średniej nieszczelności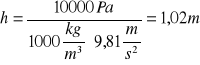

- dużej nieszczelności h = 0

3. Ze wzrostem nieszczelności maleje czas rozszczelnienia układu (następuje zrównanie ciśnień w zbiorniku i na zewnątrz zbiornika).

4. Czas zassania układu i wielkość uzyskanego podciśnienia zależą od stopnia szczelności układu.

Ze sporządzonych wykresów charakterystyki pompy
i charakterystyk nieszczelności
zauważymy, że:

1. Wydatek pompy maleje wraz ze wzrostem podciśnienia.

2. Wraz ze wzrostem nieszczelności układu rośnie wydatek nieszczelności.

3. W badanym przez nas układzie najwyższe podciśnienie uzyskaliśmy przy najmniejszej nieszczelności , co stanowi potwierdzenie wniosków opracowanych na podstawie wzorcowych pomiarów.

4. Niedokładność pomiarów, a tym samym otrzymanych charakterystyk nieszczelności wynika z braku zsynchronizowania włączenia pompy i układu rejestrującego pomiary.

5. Maksymalne wartości podciśnienia w zbiorniku odczytane na manometrze różnicowym są bardzo zbliżone do otrzymanych na wykresie.

Dysza	Wskazanie manometru różnicowego ∆p [hPa]	Wykres [hPa]
Mała	904	909
Średnia	673	672,7
Duża	122	122,7

---