Rozdział V
Różniczkowanie numeryczne
Odwracam się z przerażeniem
i ze wstrętem od tej żałosnej
plagi funkcji ciągłych
nie mających pochodnej.
Charle Hermite
5.1. Uwagi ogólne.
Zagadnienie różniczkowania numerycznego powstaje kiedy funkcja ![]()
jest określona przez tablicę albo zależność ![]()
jest bardzo skomplikowana.
Rozpoczniemy od wzoru, który bezpośrednio wynika z definicji pochodnej
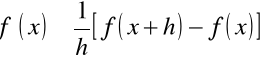
,
gdzie ![]()
i ![]()
.
Oszacujemy błąd tego przybliżenia stosując trzecią postać wzoru Taylor'a
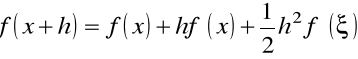
,
gdzie ![]()
. Wynika stąd, że pierwsza pochodna może być zapisana w postaci
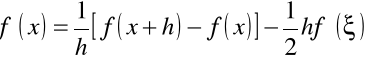
.
Pierwszy składnik ![]()
jest wartością przybliżoną pochodnej funkcji ![]()
, wówczas drugi składnik ![]()
jest błędem przybliżenia (ten składnik jeszcze nazywają błędem obcięcia).
Przykład 5.1. Dla ![]()
znaleźć przybliżoną wartość pochodnej funkcji ![]()
w punkcie ![]()
i oszacować błąd tej wartości.
Z powyższego rozważania gdy by wynika, że zawsze czym mniejsze ![]()
tym mniejszy jest błąd przybliżenia. Niestety, nie jest to „zawsze” tak. Rozważmy następny przykład.
Przykład 5.2. Znaleźć zależność przybliżonej wartości pochodnej funkcji ![]()
w punkcie ![]()
i jej błędu od wartości ![]()
. Uwzględnić, że ![]()
, ![]()
oraz ![]()
.
W tym przykładzie występuje charakterne zjawisko: czym mniejsza wartość ![]()
tym mniejsze liczb znaczących utrzymuje różnica ![]()
. Więc dla małych wartości ![]()
wątpliwe jest otrzymanie dobrych przybliżeń dla pochodnej ![]()
.
Wzory dla różniczkowania numerycznego przede wszystkim wykorzystuje się przy rozwiązaniu numerycznym równań różniczkowych. Dokładność przybliżenia odpowiednich pochodnych ocenia się używając tak zwanego wykładnika ![]()
w czynniku ![]()
błędu.
Np. Dla poprzedniego omówionego wzoru obliczenia pochodnej
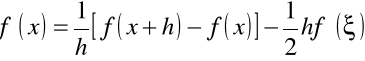
,
mamy, że wykładnik ![]()
.
Przybliżoną wartość pochodnej ![]()
funkcji ![]()
może być określona w różny sposób.
Rozważmy dla przybliżenia pochodnej następujący wzór
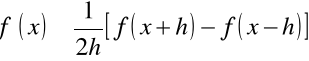
.
Ocenimy błąd tego przybliżenia. Ponieważ z trzeciej postaci wzoru Taylor'a mamy
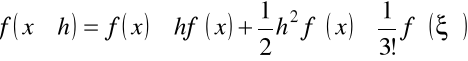
,
to dla rozważanego przybliżenia znajdziemy
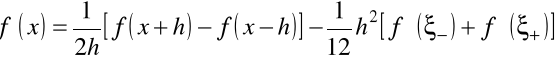
,
gdzie ![]()
i ![]()
. Jeśli trzecia pochodna jest ciągła, to zawsze istnieje takie ![]()
, że
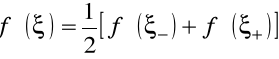
,
i wówczas
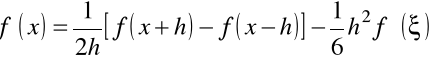
.
W rozważanym przypadku wykładnik tego przybliżenia będzie ![]()
.
Dla określenia przybliżonej wartości drugiej pochodnej możemy postępować analogiczne. Mianowicie, zapisujemy
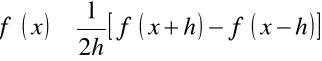
.
W podobny sposób z wykorzystaniem trzeciej postaci wzoru Taylor'a dla drugiej pochodnej znajdziemy
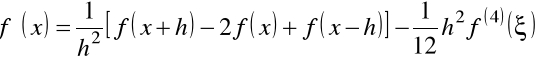
,
gdzie ![]()
.
Przykład 5.3. Znaleźć zależność przybliżonej wartości pochodnej funkcji ![]()
w punkcie ![]()
i jej błędu od wartości ![]()
na podstawie drugiego wzoru dla pochodnej. Uwzględnić, jak i wcześniej, że ![]()
, ![]()
oraz ![]()
.
5.2. Ekstrapolacja Richardsona.
Skorzystamy teraz dwa razy z szeregu Taylor'a dla funkcji ![]()
i ![]()
. Mamy
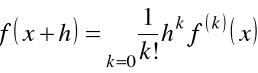
i
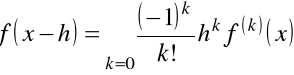
.
Odejmujemy tę wyrażenia stronami. Stadniki z parzystymi ![]()
skracają się. Z otrzymanego wyrażenia wyznaczamy pierwszą pochodną
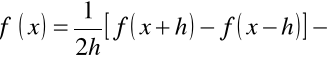
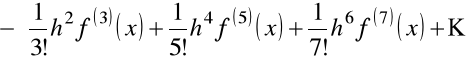
.
Otrzymane wyrażenie będziemy traktować jako pewne równanie typu
![]()
,
gdzie ![]()
oznacza pierwszą pochodną, a ![]()
jej przybliżenie, np.
![]()
.
Wówczas sumę
![]()
można rozumieć jako błąd tego przybliżenia. Jeśli ![]()
, to dla małych ![]()
składnik ![]()
dominuje nad pozostałymi. Spróbujemy go usunąć.
Dokonamy podstawienia ![]()
i otrzymany wynik pomnożymy przez 4
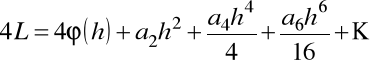
.
Od tego wyrażenia odejmujemy wyjściową postać, tzn.
![]()
,
i wynik dzielimy przez 3
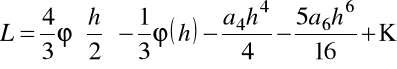
.
Przejście do tego wyrażenia jest pierwszym krokiem ekstrapolacji Richardsona.
Stwierdzamy, że prosta w obliczeniach kombinacja wartości funkcji ![]()
i ![]()
:
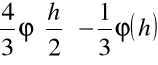
,
jest kolejnym przybliżeniem dla ![]()
, ale już z błędem ![]()
.
Na tej optymistycznej drodze możemy otrzymywać dalsze coraz lepsze oceny pochodnej.
Przykład 5.4. Znaleźć zależność przybliżonej wartości pochodnej funkcji ![]()
w punkcie ![]()
i jej błędu od wartości ![]()
z wykorzystaniem ekstrapolacji Richardsona. Uwzględnić, jak i wcześniej, że ![]()
, ![]()
oraz ![]()
.
Określimy wyrażenie
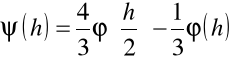
i wynik po pierwszym kroku ekstrapolacji Richardsona zapiszemy w postaci
![]()
,
gdzie wartości współczynników są oczywiste.
Dokonamy teraz znowu podstawienia ![]()
. Mamy
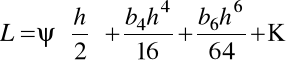
,
Mnożąc przez 16 i odejmując poprzednie wyrażenie dla pochodnej oraz dzieląc wynik przez 15, znajdziemy
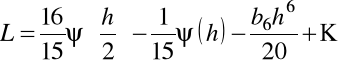
,
Znowu, określając wyrażenie
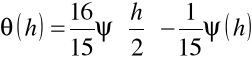
,
zapisujemy
![]()
oraz przy ![]()
znajdziemy
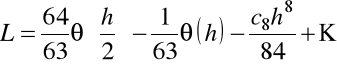
Pełny schemat metody ekstrapolacji Richardsona możemy sformułować następująco:
niech będzie określono równanie
![]()
,
wybieramy
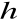
(np.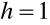
);obliczamy wielkości
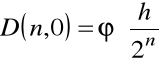
, ![]()
;
dla
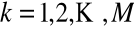
i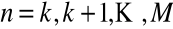
stosujemy wzór rekurencyjny
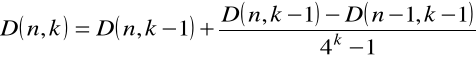
;
budujemy modyfikowane równanie dla pochodnej po
krokach ekstrapolacji.
Twierdzenie. Przy ekstrapolacji Richardsona zachodzi równość
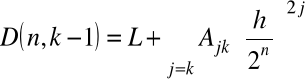
.
5.3. Różniczkowanie numeryczne za pocą wielomianów interpolacyjnych
Dla wyprowadzenia wzorów na różniczkowanie numeryczne zastępujemy w przedziale ![]()
daną funkcję ![]()
przez funkcję interpolującą ![]()
, a następne przyjmujemy
![]()
,
![]()
,
![]()
,
…………….
![]()
.
Podkreślimy, że jeśli nawet błąd interpolacji
![]()
,
jest mały, to z tego nie wynika, że błędy pochodnych
![]()
,
![]()
,
…………………
![]()
,
będą również małe.
A. Wielomiany interpolacyjne Newtona.
Ponieważ pierwszy wzór interpolacyjny Newtona ma postać
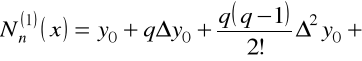
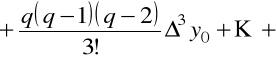
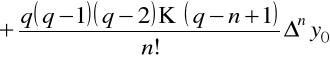
,
to dla pochodnych mamy
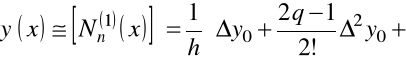
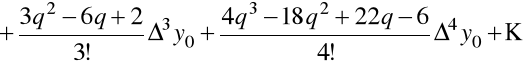
oraz
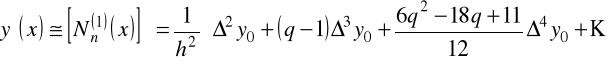
.
Przypomnimy, że ![]()
, gdzie ![]()
jest odległością pomiędzy węzłami.
Przy obliczaniu pochodnej w określonym punkcie ![]()
należę za ![]()
przyjąć najbliższą wartość tablicową argumentu.
Jeśli szukane pochodne tylko w węzłach interpolacji, to wtedy zawsze możemy tak wybrać ![]()
, żeby ![]()
. Wówczas odpowiednie wzory upraszczają się
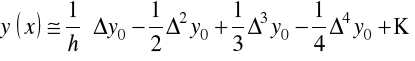
oraz
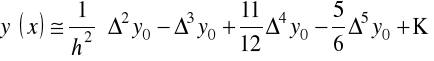
.
Przykład 5.5. Dla funkcje określonej przez tablice obliczyć pierwszą i drugą pochodną w punkcje ![]()
.
|
|
|
|
|
|
1,0 |
1,1752 |
0,1605 0,1738 0,1889 0,2059
|
0,0133 0,0151 0,0170
|
0,0018 0,0019
|
0,0001
|
1,1 |
1,3357 |
|
|
|
|
1,2 |
1,5095 |
|
|
|
|
1,3 |
1,6984 |
|
|
|
|
1,4 |
1,9043 |
|
|
|
|
Według powyższych wzorów zapisujemy
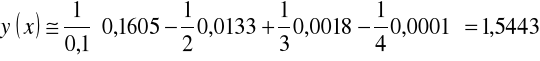
(dokładna wartość 1,5431) oraz
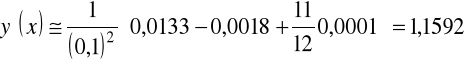
(dokładna wartość 1,1752).
Podobnie dla drugiego wzoru interpolacyjnego Newtona
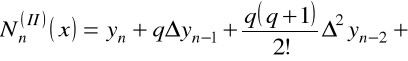
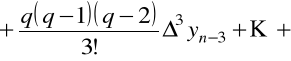
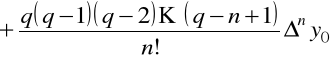
.
mamy
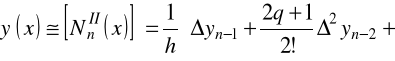
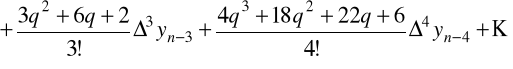
oraz
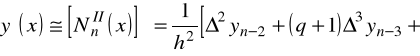
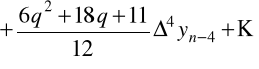
.
Dla pochodnych w węzłach interpolacji przy ![]()
otrzymamy
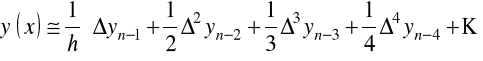
oraz
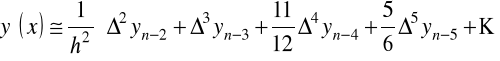
.
Przykład 5.6. Dla funkcje określonej przez tablice obliczyć pierwszą i drugą pochodną w punkcje ![]()
.
B. Wielomiany interpolacyjne Gaussa.
Podobnie określamy wzory dla pochodnych z wykorzystaniem wielomianów interpolacyjnych Gaussa.
Ponieważ pierwszy wzór interpolacyjny Gaussa ma postać
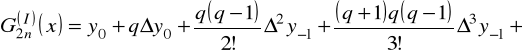
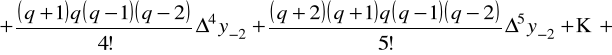
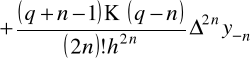
,
to dla pochodnych mamy
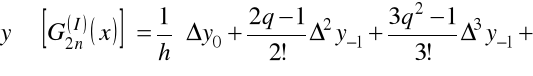
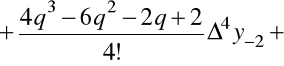
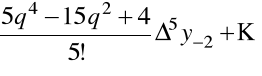
,
oraz
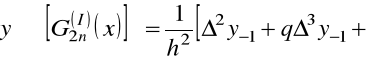
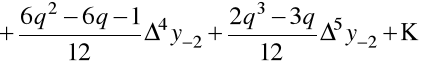
.
Dla pochodnych w węzłach interpolacji
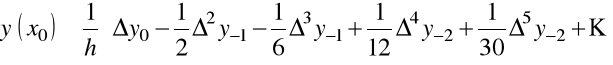
oraz
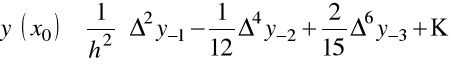
.
Ponieważ pierwszy wzór interpolacyjny Gaussa ma postać
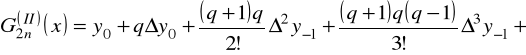
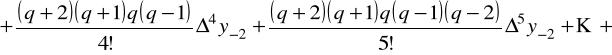
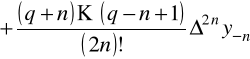
,
to dla pierwszej
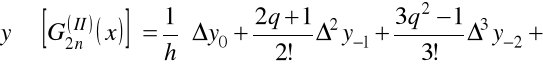
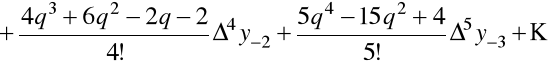
i drugiej pochodnej
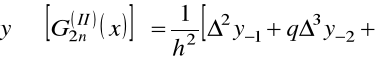
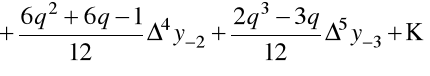
.
Przy ![]()
w węzłach mamy
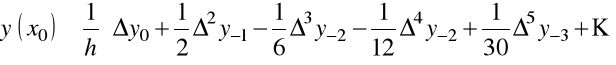
oraz
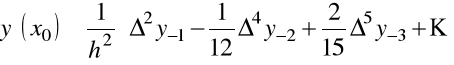
.
C. Wielomiany interpolacyjne Lagrange'a.
Wygodnie jest skorzystać z następującej ogólnej postaci wielomianów Lagrange'a
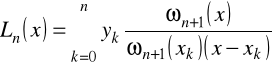
,
gdzie
![]()
,
![]()
,
oraz ![]()
, ![]()
.
Przyjmując
![]()
,
pierwszą pochodną określamy wzorem
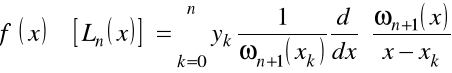
,
oraz drugą
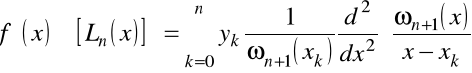
.
Wyszukiwarka
Podobne podstrony:
num 4 (1), polibuda, 4 semestr, metody numeryczne(laboratorium, wejściówki kolokwia), ćw4
Met num cz1, METODY NUMERYCZNE W ELEKTROTECHNICE
Metody numeryczne, sprawozdanie num new332 pluskwik, Piotr Próchniak gr
Notka, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody numeryczne dla zas
Macierze - teoria, Politechnika Radomska, 1 stopień, przed 5 semestrem, metody numeryczne, Wysyłka M
Zadanie 2 Met Num TM 2010, Politechnika Radomska, 1 stopień, przed 5 semestrem, metody numeryczne,
R8 Row Roz, metody numeryczne
Metody numeryczne w6
metoda siecznych, Elektrotechnika, SEM3, Metody numeryczne, egzamin metody numeryczn
MN energetyka zadania od wykładowcy 09-05-14, STARE, Metody Numeryczne, Część wykładowa Sem IV
METODA BAIRSTOWA, Politechnika, Lab. Metody numeryczne
testMNłatwy0708, WI ZUT studia, Metody numeryczne, Metody Numeryczne - Ćwiczenia
Metody numeryczne Metoda węzłowa
Metody numeryczne, wstep
metody numeryczne w4
Metody numeryczne PDF, MN macierze 01 1
więcej podobnych podstron