Rozdział VII

Rozwiązanie numeryczne równań

różniczkowych

7.1. Równania pierwszego rzędu.

Równanie Riccati'ego

Równanie to ma postać następującą

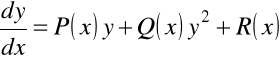
. (7.1)

Zaznaczmy, że jeśli funkcja
jest równa zero, tzn.
, to równanie Riccati'ego (7.1) sprowadza się do równania Bernoulli'ego przy
, które całkuje się analitycznie. Wówczas jeśli funkcja
jest równa zero, tzn.
, to otrzymujemy liniowe równanie różniczkowe, które też całkuje się analitycznie.

Łatwo sprawdzić, że w przypadku ogólnym możemy tak dobrać funkcje
, żeby podstawienie

,

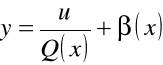
gdzie
jest nową funkcją poszukiwaną, sprowadzało równanie Riccati (7.1) do postaci kanonicznej

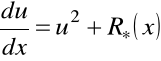
, (7.2)

gdzie funkcja
jest określona przez funkcję
,
i
.

W wielu przypadkach ułatwia to znalezienie rozwiązania ogólnego równania wyjściowego.

Zaznaczmy, że w przypadku ogólnym rozwiązanie ogólne równania (7.2) nie da się sprowadzić do skończonej liczby całek nieoznaczonych (całkowaniu przez kwadratury - Liouville).

W przypadkach szczególnych możemy wyróżnić kilka sposobów całkowania równanie Riccati'ego.

1. Jeśli znane jest rozwiązanie szczególne
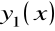
   równania (7.2), to przez podstawienie

dla funkcji z otrzymujemy równanie Bernoulli'ego.

Wówczas podstawienie

,

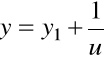
gdzie
jest nową funkcja poszukiwaną, sprowadza równanie Riccati'ego bezpośrednio do równania liniowego.

(Sprawdzić samodzielnie).

Przykład 7.1. Rozwiązać równanie

,

jeśli jego rozwiązanie cząstkowe
.

2. Jeżeli znane są dwa liniowo niezależne rozwiązania szczególne
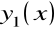
   oraz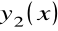
   , to dla rozwiązania ogólnego mamy

.

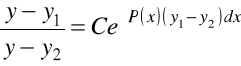
Dowód. Odejmując równania

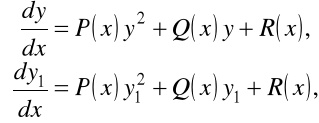
znajdziemy

.

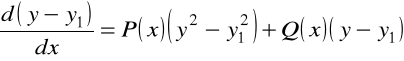
Dzieląc przez
, mamy

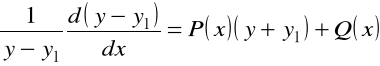
i następnie

.

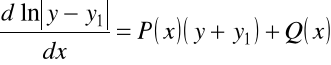
Podobnie znajdujemy, że

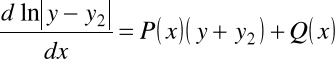
Odejmując otrzymane równania

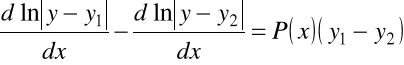
i dokonując przekształcenia

,

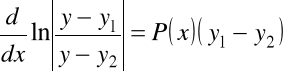
oraz całkując, mamy

.

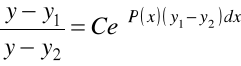
Pokaż, że w tym przypadku funkcja
jest również rozwiązaniem szczególnym równania liniowego względem z, co pozwala uprościć jego całkowanie.

Przykład 7.2. Rozwiązać równanie

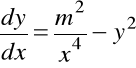
jeśli wiadome dwa jego rozwiązania cząstkowe

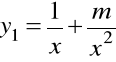
i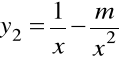
.

3. Jeśli są znane trzy liniowe niezależne rozwiązania szczególne
   ,
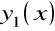
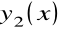
   i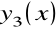
   , to całka ogólna równania Riccati'ego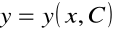
   wyznacza się z relacji

.

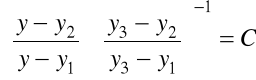
7.2. Metoda kolejnych przybliżeń Picard'a (iteracja).

Rozważmy zagadnienie Cauchy'ego

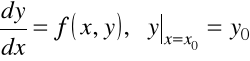
, (7.3)

oraz
.

Całkujemy równanie formalne

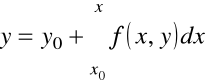
i budujemy ciąg rekurencyjny w następujący sposób

.

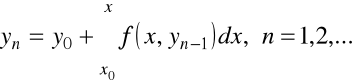
Twierdzenie 7.1. Granica ciągu rekurencyjnego jest rozwiązaniem zagadnienie Cauchy'ego, tzn.
, i dla
spełnia się nierówność

,

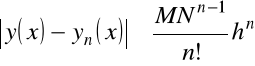
gdzie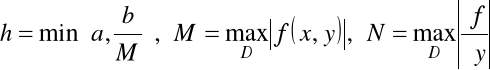
.

Przykład 7.3. Rozwiązać zagadnienie Cauchy'ego

.

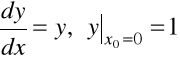
Załóżmy
i obliczmy kolejno:

,

,

,

…………………………………………………….

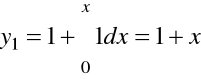
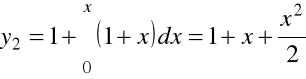
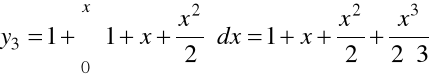
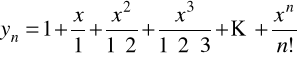
Kiedy
, to
, co odpowiada rozwiązaniu ścisłemu.

Przykład 7.4. Rozwiązać zagadnienie Cauchy'ego

,
.

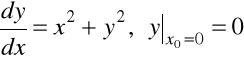
Załóżmy
i obliczmy kolejno:

,

,

,

……………………………………………………

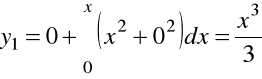
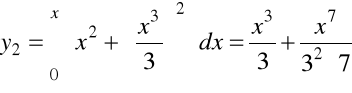
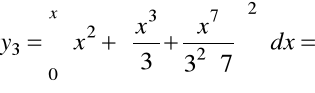
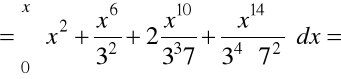
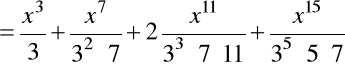
Otrzymujemy szybko zbieżny szereg.

Przykład 7.5. Rozwiązać zagadnienie Cauchy'ego

,
.

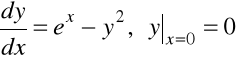
Załóżmy
i obliczmy kolejno:

,

,

,

……………………………………………………….

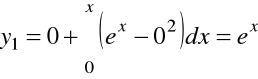
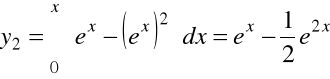
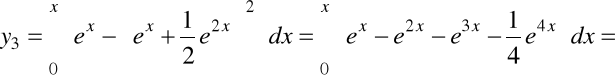
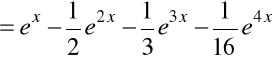
Również otrzymujemy szybko zbieżny szereg.

7.3. Całkowanie za pomocą szeregów.

Szereg Taylor'a.

Rozważamy zagadnienie Cauchy'ego (7.3), tzn.

.

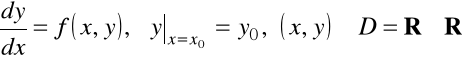
Przyjmujemy, że funkcja
może być rozwinięta w szereg Taylor'a względem
i
.

Poszukujemy rozwiązanie w postaci

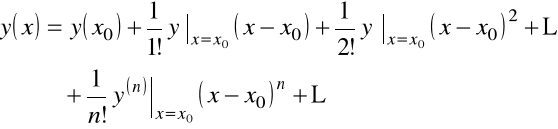
Wartości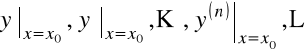
określamy bezpośrednio równania.

Przykład 7.6. Rozwiązać zagadnienie Cauchy'ego

,
.

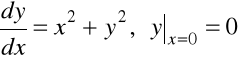
Obliczamy kolejno:

;
;
;

;

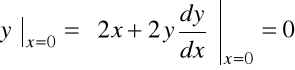
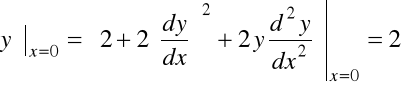
Otrzymujemy szybko zbieżny szereg.

Dokonamy pewnego uogólnienia tej metody. Przypuśćmy, że znaleźliśmy rozwiązanie w punktach
(
). Znajdziemy rozwiązanie w następnym punkcie. Zapiszemy pochodną w otoczeniu punktu

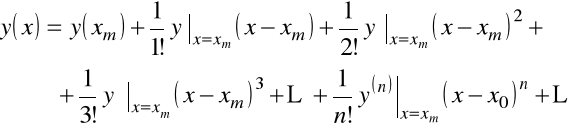
Dla punktu
ten szereg możemy przepisać następująco

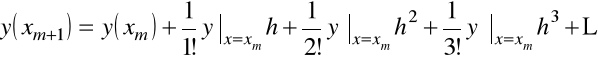
Wartość pierwszej pochodnej w punkcie
znajdujemy bezpośrednio z równania

.

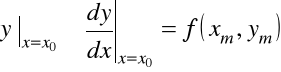
Dla znalezienia drugiej pochodnej dokonamy różniczkowania równania
. Mamy

.

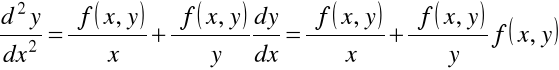
Wówczas

.

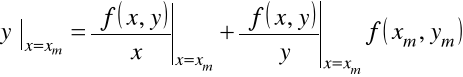
Zaznaczmy, że ponieważ kolejne pochodne są skomplikowane, to wygodnym jest określenie operatora

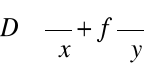
i zapisywanie kolejnych pochodnych z jego wykorzystaniem. Na przykład,

.

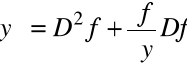
Przykład 7.7. Rozwiązać zagadnienie Cauchy'ego

,
.

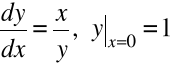
7.4. Metody Rungego-Kutty.

Rozważamy zagadnienie Cauchy'ego (7.3), tzn.

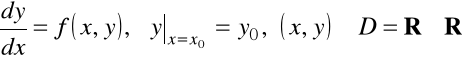
oraz rozważamy równoodlegle punkty
(
).

Podstawą wszystkich metod Rungego-Kutty jest wyko­rzystanie wzoru

,

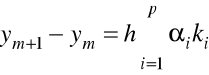
gdzie
są stałe,
, wówczas

,

,

………………………………

,
.

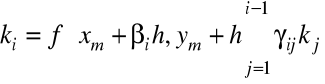
Współczynniki
dobiera się tak, żeby powyższa kombinacja liniowa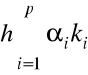
dla
była uzgodniona z odpowiednim szeregiem Taylor'a do wyrazów rzędu
.

Zaznaczmy, że liczbę
nazywa się rzędem metody Rungego-Kutty.

Ponieważ, wybór współczynników
dla danego
jest niejednoznaczny, to mówi się o rodzinie metod Rungego-Kutty rzędu
.

Jeśli
i
, to mamy wiadomą metodę Euler'a

.

Ważny przypadek cząstkowy
, kiedy rozwiązanie zagadnienia Cauchy'ego

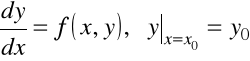
zapisuje się w postaci jawnej

.

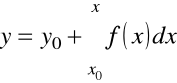
Wtedy również

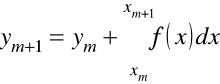
i metoda Euler'a prowadzi do równości

,

,

………………..

.

Dodając stronami otrzymamy wzór prostokątów dla obliczania całki

.

Modyfikowana metoda Euler'a

:
,
,
,
.

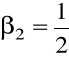
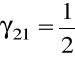
Poprawiona metoda Euler'a (metoda Heuna)

:
,
,
,
.

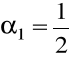
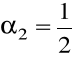
Dla metody Heuna

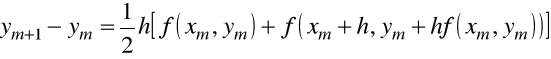
oraz dla
mamy

…………………………….

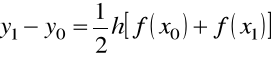
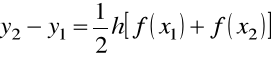
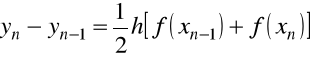
Dodając stronami otrzymamy wzór trapezów dla obliczania całki

.

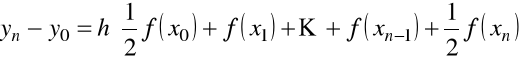
Podobnie metoda Rungego-Kutty przy
wygląda następująco

,

,

,

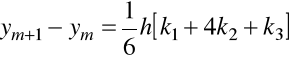
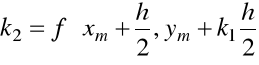
dla
prowadzi do wzoru Simpsona dla obliczania całki.

Klasyczna metoda Rungego-Kutty odpowiada
oraz następnej kombinacji liniowej

,

,

,

,

.

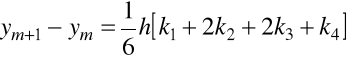
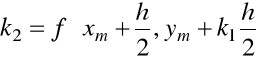
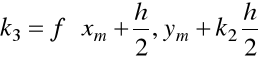
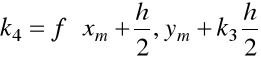
7.5. Ekstrapolacyjna metoda Adamsa.

Rozważamy zagadnienie Cauchy'ego (7.3), tzn.

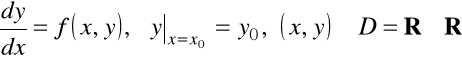
oraz weźmiemy dla rozwiązania tego równania równoodlegle punkty
(
).

Zapisujemy jego rozwiązanie w postaci formalnej dla każdego przedziału

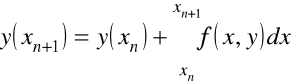
lub

.

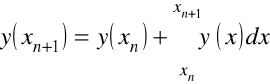
Aby znaleźć przybliżoną wartość występującej całki należę skorzystać z jakiegoś wzoru dla funkcji podcałkowej w przedziale
. Ponieważ z założenia są znane wartości tej funkcji w poprzednich punktach
, to można skorzystać z ekstrapolacji funkcji określonej w wskazanych punktach
przedziału
.

Dla pochodnej pod całką wykorzystamy drugi interpolacyjny wielomian Newtona

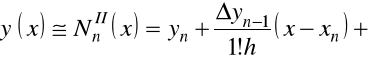
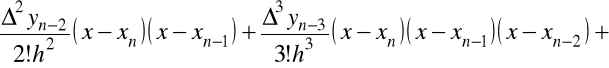
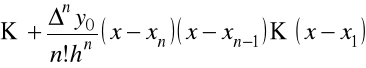
ponieważ znane są wartości funkcji
w punktach
(
).

Podstawiając i całkując, otrzymamy

.

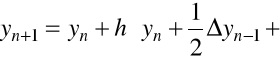
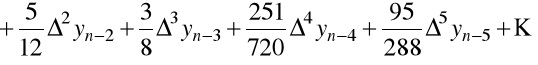
Zwykle korzysta się z metody ekstrapolacyjnej Adamsa dla
. Wtedy

.

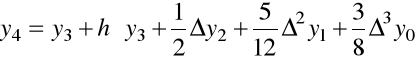
Dla skorzystania z tej metody, jak i wcześniej budujemy tablice