* Ilokrotnie należy rozcięczyć zasadę sodową 95%, aby otrzymać zasadę 5%
![]()
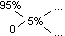
5 - 0 = 5
95 - 5 = 90
lub: R = 95 / 5 = 19 razy
Ile gramów 25% roztworu należy dodać do 350g 55% roztworu aby otrzymać roztwór 30%
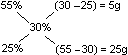
5g ↔ 55%
25 / 5 = 5 g
25g ↔ 25%
350g / 5g = 70g * 25% = 1750 g (25%)
Zadanie 1
Cytat: |
W 100 gramach roztworu cukru w wodzie znajduje się 15 gram cukru. Oblicz stężenie procentowe tego roztworu. |
Rozwiązanie:
Treść zadania nie powinna sprawiać kłopotu, gdyż jest dość oczywista. Mamy pewne naczynie - na przykład szklankę i wiemy, że znajduje się w niej 100 gram roztworu. W tych 100 gramach roztworu cukru w wodzie (czyli w osłodzonej wodzie) znajduje się 15 gram cukru. Cukier to w tym przypadku substancja rozpuszczana - jego masa wynosi 15 gram. Roztwór to natomiast wszystko to co znajduje się w szklance. Jego masa wynosi 100 g. Jeśli nie pamiętasz definicji roztworu i substancji rozpuszczanej - to koniecznie sobie je przypomnij.
Dane:
Szukane:
W jaki sposób rozwiązać to zadanie? Otóż znamy definicję stężenia procentowego (zapisaną matematycznie) - należy teraz właśnie tę definicję wykorzystać. Przypomnijmy, że wzór na stężenie procentowe można zapisać następująco:
Stężenie procentowe, Cp, jest naszą szukaną. Masę substancji rozpuszczanej, ms, znamy - podobnie jak masę roztworu (spójrz na wypisane przez nas dane i szukane). Czyli - znamy wartości wszystkich wielkości, które występują po prawej stronie naszego równania. Jeśli podstawimy do wzoru wszystko co wiemy (oczywiście w odpowiednich miejscach), to wówczas uzyskamy poprawny wynik:
Wykonując powyższe działania uzsykaliśmy wynik. Zauważ, że podczas obliczeń skróciły się nam jednostki masy (gramy z gramami), a wynik podaliśmy w procentach. Pamiętaj o tym, że zawsze należy podawać jednostki, w których wyrażone są różne wielkości. Jednostek nie należy dopisywać na końcu, po wykonanych obliczeniach - gdyż wówczas można się bardzo łatwo pomylić (czasami podczas obliczeń jednostki zmieniają się). Należy więc bezwzględnie wykonywać działania na jednostakch.
Należy jeszcze tylko podać odpowiedź do zadania:
Odpowiedź:
Stężenie procentowe roztworu jest równe 15%.
Zadanie 2
Cytat: |
W 100 gramach wody rozpuszczono 5 gram soli. Oblicz stężenie procentowe uzyskanego roztworu. |
Rozwiązanie:
Jest to kolejny przykład zadania, które wymaga od Ciebie jedynie podstawienia odpwiednich dancch do wzoru. Sytuacja w tym zadaniu nie jest jednak zupełnie identyczna z sytuacją z zadania poprzedniego. Znamy bowiem masę substancji rozpuszczanej oraz masę wody (czyli rozpuszczalnika) - nie mamy natomiast podanej masy roztworu (jeśli masz kłopoty z rozróżnieniem rozpuszczalnika od roztworu - to wróć do początkowej części artykułu). Wypiszmy zatem nasze dane i szukane:
Dane:
Szukane:
Żeby rozwiązać to zadanie korzystamy ponownie z matematcznego zapisu definicji stężenia procentowego:
Stężenie procentowe jest naszą szukaną, masę substancji rozpuszczanej znamy. Do obliczenia zadania brakuje nam tylko masy roztworu. Co robić? Nie należy wpadać w panikę - przecież wiemy, że roztwór to rozpuszczalnik i substancja rozpuszczona razem - więc i masa roztworu będzie sumą mas: rozpuszczalnika i roztworu:
Więc:
Podstawiając do wzoru:
Odpowiedź:
Stężenie procentowe roztworu jest równe 4,76 %.
Zadanie 3
|
Oblicz ile azotanu(V) potasu należy rozpuścić w 250 g wody aby otrzymać roztwór o stężeniu 10% |
Rozwiązanie:
Wspomniana w zadaniu woda jest oczywiście rozpuszczalnikiem. Wypiszmy zatem dane i szukane:
Dane:
Szukane:
Spośród trzech zmiennych wsytępujących we wzorze na stężenie porcentowe - znamy dwie. Oznacza to, że w bardzo prosty sposób możemy wyznaczyć trzecią zmienną. Można to zrobić dokonując przekształcenia wzoru na stężenie procentowe - w taki sposób aby wyznaczyć szukaną wielkość - czyli ms.
Zapisujemy równanie podstawowe:
Podstawmy do równania wielkości, które znamy:
Wyznaczmy teraz z powyższego równania ms, wykonując jednocześnie wszystkie możliwe działania:
Odpowiedź:
Należ rozpuścić 27,78 g azotanu(V) potasu.
Zadanie 4
|
Ile wody i ile soli należy użyć do sporządzenia 500 g roztworu soli w wodzie o stężeniu procentowym 1%? |
Rozwiązanie:
Zadanie to ma nieco wyższy poziom trudności niż poprzednie. Zacznijmy od wypisania tego co wiemy i tego co szukamy - byc może nakieruje to nas na prawidłową odpowiedź.
Dane:
Szukane:
Jak widzisz tym razem mamy aż dwie niewiadome, które podczas obliczeń musimy wyznaczyć. W jaki sposób to zrobić? Tym razem nie możemy skorzytać z jednego równania, gdyż nie ma nawet takiego pojedynczego równania, w którym występowało by stężenie procentowe, masa roztworu, masa substancji rozpuszczanej i masa rozpuszczalnika.
Wiemy jednak, że masa roztworu jest związana z masą substancji rozpuszczanej i masą rozpuszczalnika za pomocą równania:
Masę roztworu znamy. Gdyby w jakiś sposób udało się nam wyliczyć masę substancji rozpuszczanej lub masę rozpuszczalnika - to dzięki powyższej zależności - wyliczylibyśmy także drugą zmienną.
Popatrzmy teraz na podstawowy wzór na stężenie procentowe:
Z tego równania w bardzo prosty sposób możemy wyznaczyć masę substancji rozpuszczanej:
W ten sposób wyznaczyliśmy masę substancji rozpuszczanej.
Jak pamiętasz na masę roztworu składa się wszystko to co w tym roztworze jest. Zatem jeśli mamy w tym roztworze wodę i sól i to razem ma masę 500 g, to oznacza to, że masę wody zawartą w roztworze otrzymamy odejmując od masy całkowitej roztworu masę soli w nim zawartej:
Odpowiedź:
Należy rozpuścić 5 g soli w 495 g wody.
Zadanie 5
Cytat: |
Do 150 g roztworu azotanu(V) potasu o stężeniu 10% dodano 50 g wody. Jakie jest stężenie procentowe roztworu po rozcieńczeniu? |
Rozwiązanie:
Analiza sytuacji przedstawionej w zadaniu nie powinna nastręczać większych trudności. Do roztworu - nazwijmy go - początkowego o znanym stężeniu procentowym i znanej masie roztworu dodano pewną ilość wody. Rzecz jasna oznacza to, że zwiększyła się masa roztworu, ale masa substancji rozpuszczanej nie uległa zmianie.
Dane:
Szukane:
Naszym zadaniem jest wyznaczenie stężenia procentowego roztworu po rozcieńczeniu. Zatem, zgodnie z definicją stężenia procentowego:
Aby obliczyć stężenie procentowe roztworu po rozcieńczeniu musimy znać masę substancji rozpuszczanej i masę roztworu. Obliczenie masy substancji rozpuszczanej nie powinno być trudne - wystarczy skorzystać z przekształconego wzoru na stężenie procentowe dla roztworu początkowego:
Zauważ, że korzytsliśmy tutaj z masy roztworu początkowego i z początkowego stężenia procentowego. Masa substancji rozpuszczanej się nie zmienia w trakcie rozcieńczania roztworu wodą. Wydaje się to oczywiste, ale może warto to zaznaczyć.
Jak już zostało wspomniane - zmienia się natomiast masa roztworu. Masa roztworu po rozcieńczeniu jest równa oczywiście sumie mas roztworu początkowego oraz wody, którą dolano do roztworu:
W ten sposób poznaliśmy już wszystko co jest nam potrzebne do obliczenia stężenia procentowego roztworu po rozcieńczeniu. Zatem:
Odpowiedź:
Po rozcieńczeniu stężenie roztworu azotanu(V) potasu wynosiło 7,5%.
Zadanie 6
Cytat: |
Ile gram wody należy odparować z 300 g 5% wodnego roztworu cukru, aby stężenie cukru w tym roztworze wzrosło do 6% |
Rozwiązanie:
Pierwsza ważna obserwacja, którą warto zapamiętać - podczas odparowywania wody z roztworów (a więc podczas zatężania roztworów) stężenie tych roztworów wzrasta. Oczywiste, ale warte do podkreślenia z tych samych powodów co w Zadaniu 5.
Tym razem analiza zadania jest podobna. Podczas procesu odparowywania wody (zatężania) maleje masa roztworu, masa substancji rozpuszczanej pozostaje taka sama (bo odparowujemy wodę, a nie cukier!).
Dane:
Szukane:
Zastanówmy sie teraz w jaki sposób możmy policzyć masę wody, którą trzeba odparować. powiedzieliśmy sobie już poprzednio, że w trakcie procesu zatężania zmienia się masa wody w roztworze i oczywiście masa roztworu - ale masa substancji rozpuszczonej pozostaje taka sama, bo nie odparowujemy cukru. Zatem różnica pomiędzy większą masą roztworu (roztworem na początku) a masą roztworu mniejszą (czyli na końcu) będzie równa masie wody, którą należy odparować:
Masę roztworu początkowego znamy, musimy jeszcze wyliczyć mase roztworu końcowego. Skorzystajmy zatem z przekształconego wzoru na stężenie procentowe:
Nie znamy jednak masy substancji rozpuszczonej. Jednakże możemy ją w łatwy sposób policzyć, wykorzystując do tego stężenie procentowe początkowego roztworu:
Teraz nie stoi nic na przeszkodzie, aby policzyć masę roztworu po zatężeniu:
Mamy zatem masę roztworu końcowego, więc teram my - w końcu - możemy policzyć masę wody, którą należy odparować:
Odpowiedź
Należy odparować 50 gram wody.
Zadanie 7
Cytat: |
Oblicz stężenie roztworu powstałego przez zmieszanie 200 g 10%-owego roztworu z 100 g roztworu o stężeniu 40% |
Rozwiązanie:
Sytuacja w przedstawiona w zadaniu powinna być czytelna. Mamy dwa roztwory o różnych masach i różnych stężeniach - mieszamy je i chcemy znać stężenie procentowe powstałego w ten sposób roztworu.
Dane:
Szukane:
W jaki sposób zatem obliczyć to zadanie? Po pierwsze zapiszmy podstawowy wzór, z którego będziemy korzystać:
Czym jest zatem w naszym przypadku ms i mr? Odpowiedź na to pytanie nie powinna być trudna. Masa roztworu musi być sumą mas poszczególnych roztworów (no bo przecież te roztwory zlewamy razem - do jednego naczynia). Czyli:
A co z masą substancji rozpuszczanej? Musi być ona równa sumie mas: masie substancji rozpuszczanej z pierwszego roztworu oraz masie substancji rozpuszczanej z drugiego roztworu. Czyli:
A to przecież już potrafimy policzyć - przecież wystarczy tutaj skorzystać z przeksztłconego wzoru na stężenie procentowe:
To znaczy, że:
Stężenie procentowe końcowego roztworu policzymy teraz w łatwy sposób:
Odpowiedź:
Stężenie procentowe końcowego roztworu wynosiło 20%
Zadanie 8
Cytat: |
W jakim stosunku masowym należy zmieszać 15% roztwór kwasu siarkowego(VI) z roztworem 98%-owym, aby uzyskać roztwór o stężeniu 40% |
Rozwiązanie:
Na pierwszy rzut oka zadanie wydaje się być bardzo podobne do tego rozważanego przy okazji mieszania roztworów o różnych stężeniach. Jednakże - jeśli się głębiej przyjrzeć temu problemowi - to okazuje się, że wpadnięcie na właściwe rozwiązanie nie jest zupełnie proste. W przeciwieństwie do poprzedniego zadania mamy ściśle określone stężenie końcowe, które musimy uzyskać. Nie ma podanej natomiast żadnej masy roztworu. Co robić? Na początek wypiszmy to co wiemy i to czego nie wiemy.
Dane:
Szukane:
I co dalej? Jedną z dróg rozwiązania tego zadania będzie przyjęcie, że dysponujemy już np. 100 gramami roztworu o stężeniu 15% i obliczenie ile potrzeba nam roztworu o stężeniu 98%, aby uzyskać roztwór o żądanym stężeniu. Spróbuj samodzielnie wyliczyć w ten sposób to zadanie. Zapewne zauważysz, że taki model rozwiązania jest dosyć kłopotliwy, ponieważ trzeba dużo liczyć i w wielu miejscach może dojść do pomyłki.
Na szczęście istnieje sposób, dzięki któremu można znacznie ograniczyć obliczenia oraz znacznie zaoszczędzić na czasie. Ten sposób to krzyż stężeń lub metoda krzyża stężeń.
Ogólnie dla każdego zadania tego typu możmy zapisać krzyż stężeń, który wyglądałby następująco:
Patrząc na ten rysunek już chyba wiadomo dlaczego nazywamy to krzyżem stężeń.
Krzyż stężeń rysujemy w ten sposób, że w środku krzyża zapisujemy stężenie roztworu, które musimy uzyskać (Cx). Następnie rozmieszczamy w krzyżu dwa pozostałe stężenia - tak aby znalazły się on po lewej stronie. To czy na górze zapiszemy stężenie mniejsze czy większe od naszego Cx, to nie ma najmniejszego znaczenia. Ja zapisałem to w ten sposób.
Co robimy dalej? Otóż następnie "uzupełniamy" ramiona krzyża znajdujące się po prawej stronie. W tym celu wykonujemy odpowiednie działania - tak jak zaznaczono to na rysunku. Krótko mówiąc należy odjąć odpowienie stężenia - pamiętając o tym, że od większej liczby odejmujemy mniejszą - a nie na odwrót (nie chcemy uzyskać liczb ujemnych). W ten sposób uzyskaliśmy parę liczb: m1 i m2. Co takiego te liczby oznaczają? Otóż stosunek tych liczb, tzn.:
oznacza stosunek masowy w jakim należy zmieszać roztwór o stężeniu C1 z roztworem o stężeniu C2, aby uzyskać roztwór o stężeniu Cx.
Innymi słowy uzyskamy odpowiedź, że aby dostać roztwór o stężeniu Cx należy zmieszać roztwór 1 z roztworem 2 w stosunku "takim a takim".
Zobaczmy zatem w jaki sposób policzyć nasze zadanie przy wykorzystaniu krzyża stężeń. Zacznijmy od narysowania takiego krzyża:
Jak widać - postępując w sposób opisany powyżej uzyskaliśmy, że stosunek masowy w jakim należy zmieszać roztwór o stężeniu 15% z roztworem o stężeniu 98% jest równy:
Oznacza to, że należało by zmieszać 58 części masowych roztworu mniej stężonego z 25 częściami masowymi roztworu bardziej stężonego. Lub inaczej: oba roztwory należałoby zmieszać w stosunku masowym 2,32:1.
Odpowiedź:
Roztwór 1 z roztworem 2 należy zmieszać w stosunku masowym 2,32:1.
Zadanie 9
Cytat: |
Oblicz jaką ilość roztworu kwasu solnego o stężeniu 10% i jaką ilość kwasu solnego o stężeniu 30% należy użyć do przygotowania 500 g roztworu o stężeniu 25% |
Rozwiązanie:
Zadanie to jest bardzo podobne do zadania popzedniego. tym razem jednak musimy przyrządzić konkretną ilość roztworu - więc nasza odpowiedź nie może zawierać jedynie stosunku masowego, w którym należy zmieszać ze sobą dwa roztwory - ale również konkretne ilości tych roztworów.
Zadanie liczymy podobnie jak poprzednio.
Dane:
Szukane:
Na początek musimy policzyć stosunek masowy w jakim należy zmieszać ze sobą dwa roztwory. W tym celu układamy krzyż stężeń:
Jak widać z krzyża stężeń - stosunek masowy w jakim musimy zmieszać roztwór 1 (o mniejszym stężeniu) z roztworem 2 (o stężeniu większym) jest równy:
Co oznacza taki zapis? Możemy go odczytać w ten sposób, że należ zmieszać ze sobą 1 część masową roztworu o stężeniu 10% z 3 częściami masowymi roztworu o stężeniu 30%. My musimy mieć 500 gram roztworu końcowego. W jaki sposób to osiągnąć? Nie jest to trudne. Wiemy bowiem, że mieszamy 1 część masową jednego rotworu i 3 części masowe drugiego roztworu. Razem więc - 4 części masowe. Te 4 części masowe muszą stanowić 500 g. Innymi słowy:
Wynika z tego, że nasza 1 część masowa jest równa 125 g. Mieliśmy wziąć 1 część masową roztworu o stężeniu 10%, czyli:
oraz 3 części masowe roztworu o stężeniu 30%, czyli:
Odpowiedź:
Należy użyć 125 g roztworu o stężeniu 10% i 375 g roztworu o stężeniu 30%
Wyszukiwarka
Podobne podstrony:
A ściąga na uboczne 2010, Studia - materiały, semestr 7, Uboczne
Surowce rzeźne, Studia - materiały, semestr 7, Uboczne
do nauki na egzam9, Studia - materiały, semestr 5, Technologia roślinna
WSZECHWIEDZA OC, Politechnika Poznańska, Studia- materiały, Semestr 2, Obróbka plastyczna- wykłady,
WSZECHWIEDZA S i OC, Politechnika Poznańska, Studia- materiały, Semestr 2, Obróbka plastyczna- wykła
wpływ opakowań na jakość i trwałość mleka spożywczego(1), Studia - materiały, semestr 7, Projektowan
pytania na matbud 1, STUDIA budownictwo, SEMESTR II, materiały budowlane
zadania na cwiczenia 2[1], Studia - Mechatronika, III semestr, Elektrotechnika
WSZECHWIEDZA S, Politechnika Poznańska, Studia- materiały, Semestr 2, Obróbka plastyczna- wykłady, M
Kanały dystrybucji na rynku zbóż przed integracją z UE - praca, Studia - materiały, semestr 7, Zarzą
ściąga 2, Studia - materiały, semestr 6, Technologia rybna
3. Metody prewencji nieprawidłowego żywienia, Studia - materiały, semestr 7, Podstawy żywienia, Diet
elektrotech test zeszly rok + zadanie na ten test, Uczelnia, semestr2, elektronika
Biznes plan - praca zaliczeniowa, Studia - materiały, semestr 7, Zarządzanie, Marketing, Ekonomia, F
PIEKARNIA, Studia - materiały, semestr 7, Projektowanie
zadania na kolokwium informatyka, gik, semestr 4, informatyka
więcej podobnych podstron