MATERIAŁY POMOCNICZE
DO MATURY
Z MATEMATYKI
1. Zbiory. Działania na zbiorach.
Zbiór, element zbioru - pojęcia pierwotne.
Jeśli x należy do ( jest elementem ) zbioru A, to piszemy x∈A, jeśli y nie należy do zbioru A, piszemy y∉A.
Każdy zbiór jest wyznaczony przez swoje elementy.
Zbiór skończony - zbiór o skończonej liczbie elementów.
Zbiór pusty ( symbol ∅ ) - zbiór, do którego nie należy żaden element.
Zbiór nieskończony - zbiór, który nie jest ani skończony, ani pusty.
Równość zbiorów:
A = B ⇔ (dla każdego x : x∈A ⇔ x∈B )
Zawieranie się zbiorów, podzbiory:
A ⊂ B ⇔ ( dla każdego x: x∈A ⇒ x∈B )
Zbiory rozłączne - zbiory nie mające żadnego elementu wspólnego.
Suma zbiorów A ∪ B:
x∈A ∪ B ⇔ ( x∈A lub x∈B )
Iloczyn zbiorów A ∩ B:
x∈A ∩ B ⇔ ( x∈A i x∈B )
Różnica zbiorów A \ B:
x∈A \ B ⇔ ( x∈A i x∉B )
Dopełnienie zbioru A ( symbol A' ):
Jeśli wszystkie rozpatrywane przez nas zbiory są podzbiorami ustalonego zbioru X, to zbiór X nazywamy przestrzenią.
Jeśli X jest przestrzenią i A ⊂ X, to A' = X \ A
Iloczyn kartezjański ( produkt ) zbiorów A × B:
Parę elementów (x,y), w której wyróżniono element x jako pierwszy nazywamy parą uporządkowaną.
( x, y )∈A×B ⇔ ( x∈A i y∈B )
Zestawienie niektórych praw rachunku zbiorów:
nazwa prawa |
treść prawa |
przemienność dodawania |
A ∪ B = B ∪ A |
przemienność iloczynu |
A ∩ B = B ∩ A |
łączność dodawania |
(A ∪ B) ∪ C = A ∪ (B ∪ C) |
łączność iloczynu |
(A ∩ B) ∩ C = A ∩ (B ∩ C) |
rozdzielność mnożenia względem dodawania |
(A ∪ B) ∩ C =(A ∩ C) ∪ (B ∩ C) |
rozdzielność dodawania względem mnożenia |
(A ∩ B) ∪ C =(A ∪ C) ∩ (B ∪ C) |
prawa de'Morgana |
(A ∩ B)' = A' ∪ B' (A ∪ B)' = A' ∩ B' |
2. Układy równań i nierówności.
Wartość bezwzględna liczby rzeczywistej
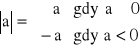
Nierówności z wartością bezwzględną
![]()
< a , to x∈( -a, a ) ![]()
> a , to x∈( -∞, -a ) ∪ ( a, ∞ )
![]()
, to x∈[ -a, a ] ![]()
, to x∈( -∞, -a ] ∪ [ a, ∞ )
Rozwiązywanie układów równań liniowych
Rozwiązaniem układu równań liniowych ( stopnia pierwszego ) z dwiema niewiadomymi nazywamy każdą uporządkowaną parę liczb spełniających oba równania układu.
Dany jest układ równań 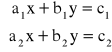
(*)
Wyznacznikami układu nazywamy liczby:
W = 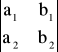
= a1 ⋅ b2 - a2 ⋅ b1;
Wx = 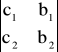
= c1 ⋅ b2 - c2 ⋅ b1;
Wy = 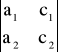
= a1 ⋅ c2 - a2 ⋅ c1;
Układ równań (*) nazywamy układem równań:
niezależnych ⇔ W ≠ 0, to układ ma dokładnie jedno rozwiązanie dane wzorami:
x = ![]()
, y =![]()
,
geometryczną interpretacją układu są dwie proste przecinające się,
zależnych ⇔ W = 0 i Wx = 0 i Wy = 0, to układ ma nieskończenie wiele rozwiązań ( x, y ) takich, że x∈R, a y = −
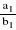
x +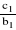
;
geometryczną interpretacją układu są dwie proste pokrywające się;
sprzecznych ⇔ W = 0 i Wx ≠ 0 lub Wy ≠ 0, zbiór rozwiązań układu jest zbiorem pustym, geometryczną interpretacją układu są dwie różne proste równoległe.
3. Funkcja kwadratowa.
Funkcją kwadratową ( trójmianem kwadratowym ) nazywamy funkcję f określoną wzorem postaci
f(x) =ax2+bx+c,
gdzie a, b, c ∈ R i a ≠ 0.
Kanoniczną postacią trójmianu kwadratowego nazywamy postać
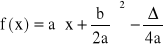
,
gdzie Δ =b2-4ac. Liczbę Δ nazywamy wyróżnikiem trójmianu.
Miejsca zerowe funkcji kwadratowej:
funkcja kwadratowa ma dwa różne miejsca zerowe x1, x2 wtedy i tylko wtedy, gdy Δ>0, wtedy
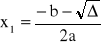
,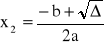
,funkcja kwadratowa ma dokładnie jedno miejsce zerowe x1 wtedy i tylko wtedy, gdy Δ=0,
![]()
,
funkcja kwadratowa nie ma miejsc zerowych wtedy i tylko wtedy, gdy Δ<0.
Iloczynowa postać funkcji kwadratowej:
jeżeli Δ>0, to trójmian kwadratowy y = ax2+bx+c (a≠0) można przedstawić w postaci iloczynu y = a(x-x1)(x-x2),
gdzie x1, x2 oznaczają miejsca zerowe trójmianu;
jeżeli Δ=0, to trójmian kwadratowy y= ax2+bx+c (a≠0) można przedstawić w postaci iloczynu
y = a(x-x1)2,
gdzie x1 jest miejscem zerowym trójmianu.
Wzory Viete'a
Jeżeli trójmian kwadratowy y= ax2+bx+c (a≠0) ma miejsce zerowe (dwa lub jedno) x1, x2, to
![]()
,
![]()
.
Wykres funkcji kwadratowej y= ax2+bx+c, gdzie a≠0, jest krzywą zwaną parabolą. Wierzchołek paraboli ma współrzędne: ![]()
.
Dla a < 0 wierzchołek paraboli jest maksimum funkcji kwadratowej, natomiast dla a > 0 wierzchołek paraboli jest minimum funkcji kwadratowej.
a > 0 a >0 a > 0 a < 0 a < 0 a < 0
Δ < 0 Δ = 0 Δ > 0 Δ < 0 Δ = 0 Δ > 0
4. Wielomiany
Wielomianem stopnia n jednej zmiennej nazywamy funkcję W:R→R określoną wzorem postaci:
W(x)=a0+a1x+a2x2+...+anxn,
gdzie a0, a1, a2, ..., an ∈ R i an≠0, n ∈ N.
Liczby a0, a1, a2, ..., an nazywamy współczynnikami wielomianu W.
Dwa wielomiany są równe wtedy i tylko wtedy, gdy są tego samego stopnia i mają równe współczynniki przy odpowiednich potęgach zmiennej.
Wielomian W jest podzielny przez wielomian W1 jeśli istnieje wielomian Q taki, że
W(x) = W1(x)⋅Q(x) dla każdego x ∈ R.
Dla każdej pary wielomianów W i W1 takich, że stopień wielomianu W1 jest dodatni, istnieje dokładnie jeden układ wielomianów Q i R, dla których W(x)=W1(x)⋅Q(x)+R(x) ( dla każdego
x ∈ R ) i stopień wielomianu R jest mniejszy od stopnia wielomianu W1 lub wielomian R jest zerowy. Wielomian R nazywa się resztą z dzielenia wielomianu W przez wielomian W1.
Reszta z dzielenia wielomianu W przez dwumian postaci ( x - r ), gdzie r ∈ R, jest równa liczbie W(r).
Twierdzenie Bézouta. Liczba a jest pierwiastkiem wielomianu W wtedy i tylko wtedy, gdy wielomian W jest podzielny przez dwumian ( x -a ).
Jeżeli liczba wymierna ![]()
jest miejscem zerowym wielomianu W(x)=a0+a1x+a2x2+...+anxn, gdzie an≠0, to q jest dzielnikiem współczynnika an, zaś p jest dzielnikiem współczynnika a0.
5. Funkcja wykładnicza i logarytmiczna
Funkcją wykładniczą jednej zmiennej nazywamy funkcję f: ( R ) → R+ określoną wzorem postaci:
f ( x ) = ax, gdzie a∈R+ .
Własności funkcji wymiernej:
Funkcja f ( x ) = ax przyjmuje tylko wartości dodatnie;
Funkcja f ( x ) = ax jest rosnąca gdy a > 1;
Funkcja f ( x ) = ax jest stała gdy a = 1;
Funkcja f ( x ) = ax jest malejąca gdy 0 < a < 1.
Równania i nierówności wymierne:
Jeżeli a > 0 i a ≠ 1 oraz ax = ay to x = y;
Jeżeli a > 1 oraz ax > ay ( ax < ay ) to x > y ( x < y );
Jeżeli a > 1 oraz ax ≥ ay ( ax ≤ ay ) to x ≥ y ( x ≤ y );
Jeżeli 0 < a < 1 oraz ax > ay ( ax < ay ) to x < y ( x > y );
Jeżeli 0 < a < 1 oraz ax ≥ ay ( ax ≤ ay ) to x ≤ y ( x ≥ y ).
Logarytm dodatniej liczby b przy podstawie a ( a > 0 i a ≠ 1 ) jest to wykładnik potęgi, do której należy podnieść a, żeby otrzymać b:
log a b = z ⇔ az = b.
Z określenia logarytmu wynika, że log a 1 = 0, log a a = 1.
Funkcją logarytmiczną jednej zmiennej nazywamy funkcję f: ( R+ ) → R określoną wzorem postaci:
f ( x ) = log a x, gdzie a∈R+\{1}.
Własności funkcji wymiernej:
Funkcja f ( x ) = log a x jest rosnąca gdy a > 1;
Funkcja f ( x ) = log a x jest malejąca gdy 0 < a < 1.
Twierdzenia o logarytmach:
Jeśli a, b, c∈R+ i a ≠ 1, to log a (b⋅c) = log a b + log a c oraz log a
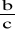
= log a b - log a c;Jeśli a, b ∈R+ , a ≠ 1 i r∈R, to log a br = r log a b;
Jeśli a, b, x∈R+ , a ≠ 1 i b ≠ 1, to log a b =
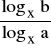
( zmiana podstawy logarytmu ).
6. Funkcje trygonometryczne
Jeśli α jest miarą kąta skierowanego ![]()
, P jest dowolnym punktem końcowego ramienia tego kąta ( P ≠ O, x i y są współrzędnymi P, ![]()
, to
sin α = ![]()
, cos α = ![]()
, tg α = ![]()
( gdy x ≠ 0 ), ctg α = ![]()
( gdy y ≠ 0 ).
Związki między funkcjami tego samego kąta x:
sin2x + cos2x = 1, dla x∈ R,
tg x = ![]()
, dla x ≠(2k+1)⋅![]()
, k∈C,
ctg x = ![]()
, dla x ≠ kΠ, k∈C,
tg x ⋅ ctg x = 1, dla x≠k⋅![]()
, k∈C.
Funkcje trygonometryczne kąta podwójnego:
sin 2x = 2⋅sin x⋅cos x,
cos 2x = cos2x - sin2x = 1 - 2sin2x = 2 cos2x - 1,
tg 2x = 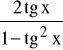
, dla x≠(2k+1)⋅![]()
i x≠(2k+1)⋅![]()
, k∈C,
ctg 2x = 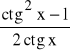
, dla x≠k⋅![]()
, k∈C.
Funkcje trygonometryczne są okresowe. Okresem zasadniczym funkcji sinus i cosinus jest 2Π, a okresem zasadniczym funkcji tangens i cotangens jest Π.
Równania trygonometryczne są to równania, w których niewiadome występują pod znakami funkcji trygonometrycznych.
Tabela zawiera rozwiązania najprostszych równań trygonometrycznych:
Równanie |
Rozwiązanie |
x0 jedyne rozwiązanie równania należące do przedziału |
sin x = a, |a|<1 |
x = kΠ+(-1)kx0, k∈C |
|
cos x = a, |a|<1 |
x = 2kΠ ± x0, k∈C |
( 0, Π ) |
tg x = a, a∈R |
x = kΠ + x0, k∈C |
|
ctg x = a, a∈R |
x = kΠ + x0, k∈C |
|
7. Funkcje wymierne. Równania i nierówności wymierne.
Funkcją wymierną jednej zmiennej nazywamy funkcję F: ( R \ A ) → R określoną wzorem postaci:
![]()
,
gdzie W i W1 są wielomianami, zaś A jest zbiorem wszystkich miejsc zerowych wielomianu W1.
Równaniem wymiernym nazywamy równanie postaci:
![]()
,
gdzie W i W1 są wielomianami.
Rozwiązaniem równania ![]()
nazywamy każdą liczbę r, dla której W1(r)≠0 i W(r)=0.
Nierównością wymierną nazywamy nierówność postaci
![]()
, lub ![]()
, lub ![]()
, lub ![]()
,
gdzie W i W1 są wielomianami.
Nierówności
![]()
, ![]()
są równoważne odpowiednio nierównościom w postaci iloczynu:
W(x)⋅W1(x)>0, W(x)⋅W1(x)<0.
Natomiast nierówności
![]()
, ![]()
są równoważne odpowiednio układom:
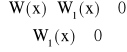
, 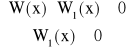
.
8. Ciągi
Zasada indukcji matematycznej ( zupełnej )
Jeżeli twierdzenie, które dotyczy liczb naturalnych, jest
prawdziwe dla ustalonej liczby naturalnej n0,
jeżeli dla każdej liczby naturalnej k ≥ n0 z założenia prawdziwości twierdzenia dla k wynika, że jest ono prawdziwe dla liczby następnej k + 1,
to twierdzenie jest prawdziwe dla każdej liczby naturalnej n ≥ n0.
Ciągiem nieskończonym nazywamy funkcję określoną na zbiorze liczb naturalnych dodatnich ( N \ { 0 } ). Wartości tej funkcji nazywamy wyrazami ciągu i oznaczamy f ( n ) = an. Jeżeli wyrazy ciągu są liczbami rzeczywistymi , to ciąg nazywamy ciągiem liczbowym.
Ciąg o wyrazach a1, a2,..., an, ... oznaczamy ( an ).
Ciąg liczbowy ( an ) nazywamy:
ciągiem rosnącym wtedy i tylko wtedy gdy dla każdego n∈N\{0} zachodzi an < an+1;
ciągiem malejącym wtedy i tylko wtedy gdy dla każdego n∈N\{0} zachodzi an > an+1;
ciągiem niemalejącym wtedy i tylko wtedy gdy dla każdego n∈N\{0} zachodzi an ≤ an+1;
ciągiem nierosnącym wtedy i tylko wtedy gdy dla każdego n∈N\{0} zachodzi an ≥ an+1.
Ciągi rosnące lub malejące nazywamy monotonicznymi.
Granice ciągu
Liczba g jest granicą ciągu liczbowego ( an ) wtedy i tylko wtedy, gdy do każdego otoczenia liczby g należą wszystkie wyrazy tego ciągu z wyjątkiem skończonej ich ilości.
![]()
.
Ciąg liczbowy ( an ) jest rozbieżny do +∞ wtedy i tylko wtedy, gdy dla każdej liczby A wszystkie wyrazy tego ciągu oprócz skończonej ich ilości są większe od A..
![]()
.
Ciąg liczbowy ( an ) jest rozbieżny do -∞ wtedy i tylko wtedy, gdy dla każdej liczby B wszystkie wyrazy tego ciągu oprócz skończonej ich ilości są mniejsze od B..
![]()
.
Prawdziwe są następujące twierdzenia:
Jeżeli
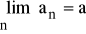
i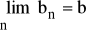
, to:
a) ![]()
= a + b, b) ![]()
= a - b,
c) ![]()
= a ⋅ b, d) jeżeli![]()
, to![]()
.
Jeżeli dla każdego n∈N\{0} an > 0 i
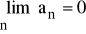
, to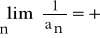
.Jeżeli dla każdego n∈N\{0} an < 0 i
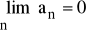
, to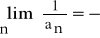
.Jeżeli
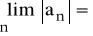
, to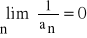
.Jeżeli
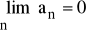
i ciąg ( bn ) jest ciągiem ograniczonym, to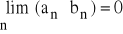
.
9. Ciągi arytmetyczny i geometryczny
Ciąg arytmetyczny
Ciąg ( an ) nazywamy arytmetycznym wtedy i tylko wtedy, gdy różnica między dowolnym wyrazem ciągu a wyrazem bezpośrednio go poprzedzającym, jest stała dla danego ciągu.
an+1 - an = r
Dla dowolnego ciągu ( an ) przez Sn oznaczamy sumę pierwszych n wyrazów tego ciągu, tzn.
Sn = a1 + a2 + ... + an.
Jeżeli ciąg ( an ) jest ciągiem arytmetycznym o różnicy r, to prawdziwe są wzory:
dla każdego n∈N\{0} an = a1 + ( n - 1 ) r,
dla każdego n∈N\{0} an =
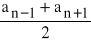
,dla każdego n∈N\{0} Sn =
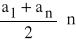
=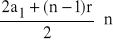
.
Ciąg geometryczny
Ciąg ( an ) nazywamy geometrycznym wtedy i tylko wtedy, gdy a1 ≠ 0 i iloraz dowolnego wyrazu tego ciągu i wyrazu bezpośrednio go poprzedzającego, jest dla danego ciągu stały.
![]()
= q
Jeżeli ciąg ( an ) jest ciągiem geometrycznym o ilorazie q ≠ 0, to prawdziwe są wzory:
dla każdego n∈N\{0} an = a1 ⋅qn-1,
dla każdego n∈N\{0} an2 = an-1⋅an+1,
jeżeli q ≠ 1, to Sn = a1
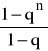
,jeżeli q = 1, to Sn = n ⋅ a1.
Dla ciągu geometrycznego ( an ) spełniającego warunek q < 1 zachodzi:
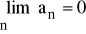
,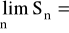
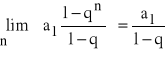
.
10. Granica funkcji. Funkcje ciągłe.
1. Granica funkcji w punkcie
Liczba g jest granicą funkcji f w punkcie x0 wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) takiego, że xn ∈ Df , xn ≠ x0 i ![]()
jest ![]()
.
2. Granice jednostronne funkcji w punkcie
a) Liczbę a nazywamy granicą lewostronną funkcji f w punkcie x0 wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) spełniającego warunki xn ∈ Df , xn < x0 i ![]()
jest ![]()
.
b) Liczbę b nazywamy granicą prawostronną funkcji f w punkcie x0 wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) spełniającego warunki xn ∈ Df , xn > x0 i ![]()
jest ![]()
.
c) Istnienie granic jednostronnych funkcji w punkcie x0 i ich równość jest równoważna istnieniu granicy funkcji w punkcie x0.
3. Granica niewłaściwa funkcji w punkcie
a) Funkcja f ma w punkcie x0 granicę niewłaściwą +∞ wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) takiego, że ![]()
, xn ∈ Df i xn ≠ x0 jest ![]()
.
b) Funkcja f ma w punkcie x0 granicę niewłaściwą -∞ wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) takiego, że ![]()
, xn ∈ Df i xn ≠ x0 jest ![]()
.
4. Twierdzenia o granicy funkcji w punkcie
Jeżeli ![]()
i ![]()
, to:
a) ![]()
= a + b, b) ![]()
= a - b,
c) ![]()
= a ⋅ b, d) jeżeli b≠0, to![]()
.
5. Granica funkcji w +∞ oraz w -∞
a) Mówimy, że granicą funkcji y = f(x) w +∞ jest liczba g wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) spełniającego warunki xn ∈ Df i ![]()
jest ![]()
.
b) Mówimy, że granicą funkcji y = f(x) w -∞ jest liczba g wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) spełniającego warunki xn ∈ Df i ![]()
jest ![]()
.
6. Ciągłość funkcji
Funkcja f jest ciągła w punkcie x0 ∈ Df wtedy i tylko wtedy, gdy istnieje granica funkcji w punkcie x0 i ![]()
.
Funkcja f jest ciągła w zbiorze Z ⊂ Df wtedy i tylko wtedy, gdy jest ciągła w każdym punkcie zbioru Z.
Jeżeli funkcje f i g są ciągłe w punkcie x0, to funkcje f + g, f - g, f ⋅ g też są ciągłe w tym punkcie, i jeżeli g(x0) ≠ 0, to funkcja ![]()
też jest ciągła w x0.
11. Pochodna funkcji i jej zastosowania
Ilorazem różnicowym funkcji f odpowiadającym przyrostowi argumentu Δx = x1 - x0, gdzie x0, x1∈ Df i x0 ≠ x1, nazywamy liczbę ![]()
.
Jeżeli przy powyższym istnieje granica ![]()
i jest liczba skończoną, to tę liczbę nazywamy pochodną funkcji w punkcie x0 i oznaczamy f '(x0).
Jeżeli funkcja ma pochodną w punkcie x0, to mówimy, że jest w tym punkcie różniczkowalna.
Jeżeli funkcja y = f(x) jest określona w pewnym otoczeniu punktu x0 i ma w tym punkcie pochodną, to prosta o równaniu:
y = f '(x) ⋅ ( x - x0 ) + f(x0)
jest prostą styczną do wykresu funkcji f w punkcie P ( x0, f(x0) ). f '(x0) jest tangensem kąta nachylenia tej stycznej do osi 0X.
Jeżeli przez X oznaczymy zbiór tych argumentów, dla których istnieje pochodna funkcji f, wówczas funkcję, która każdemu x ∈ X przyporządkowuje liczbę f '(x) nazywamy pochodną funkcji f. Dziedziną funkcji f ' jest zbiór X.
Jeżeli funkcje f i g są różniczkowalne w zbiorze X, to:
( k⋅ f )' = k ⋅ f ', dla k ∈ R
( f + g )' = f ' + g'
( f - g )' = f ' - g'
( f ⋅ g )' = f '⋅ g + g'⋅ f
Pochodne niektórych funkcji:
( c )' = 0
( x m )' = m xm-1, dla m ∈ W \{0}
( sin x )' = cos x
( cos x )' = - sin x
( tg x )' =
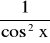
( ctg x )' = -
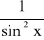
Jeśli funkcja f jest różniczkowalna w każdym punkcie pewnego zbioru X ⊂ R, a funkcja g w każdym punkcie y0 = f(x) zbioru wartości funkcji f, to dla x ∈ X pochodna funkcji złożonej h = g ◦ f równa się iloczynowi pochodnej funkcji zewnętrznej g i pochodnej funkcji wewnętrznej f:
( g ◦ f )'(x) = g'(f(x)) ⋅ f '(x).
Jeżeli funkcja f jest różniczkowalna w zbiorze Z ⊂ Df i pochodna funkcji f jest różniczkowalna, to pochodną funkcji f ' nazywamy drugą pochodną funkcji f i oznaczamy f ''.
12. Badanie funkcji
Twierdzenia o monotoniczności funkcji
Niech funkcja f będzie różniczkowalna w przedziale ( a, b ), wtedy dla każdego x ∈ ( a, b )
jeżeli f '(x) > 0, to funkcja f jest rosnąca w przedziale ( a, b );
jeśli f jest rosnąca w przedziale ( a, b ), to f '(x) ≥ 0;
jeżeli f '(x) < 0, to funkcja f jest malejąca w przedziale ( a, b );
jeśli f jest malejąca w przedziale ( a, b ), to f '(x) ≤ 0.
Ekstremum funkcji
Mówimy, że funkcja ma w punkcie x0 ∈ Df minimum ( maksimum ), jeśli dla każdego x należącego do pewnego otoczenia punktu x0 zawartego w dziedzinie funkcji zachodzi f(x) > f(x0)
( f(x) < f(x0) ). Maksimum i minimum nazywamy ekstremum funkcji.
Warunek konieczny ekstremum. Jeżeli funkcja f ma ekstremum w punkcie x0 ∈ ( a, b ) i jest w tym punkcie różniczkowalna, to
f '(x0) = 0.
Warunek wystarczający ekstremum. Jeżeli funkcja f ma pochodną w pewnym otoczeniu punktu x0, przy czym
f '(x) > 0 gdy x < x0 i f '(x) < 0 gdy x > x0
to w punkcie x0 funkcja f ma maksimum; jeżeli natomiast
f '(x) < 0 gdy x < x0 i f '(x) > 0 gdy x > x0
to w punkcie x0 funkcja f ma minimum.
Najmniejsza i największa wartość funkcji w przedziale
Mówimy, że funkcja f określona w przedziale < a, b > osiąga w tym przedziale wartość największą ( najmniejszą ), jeśli istnieje punkt x0 ∈ < a, b > taki, że dla każdego x ∈ < a, b > i x ≠ x0 spełniony jest warunek f(x) ≤ f(x0) ( f(x) ≥ f(x0) ).
Aby wyznaczyć największą ( najmniejszą ) wartość funkcji w przedziale < a, b >, należy znaleźć wszystkie maksima ( minima ) lokalne w tym przedziale oraz obliczyć f(a) i f(b); największa ( najmniejsza ) z tych liczb jest liczbą poszukiwaną.
Asymptoty wykresu funkcji
Prostą, której odległość od wykresu danej funkcji f zmierza do zera w nieskończoności nazywamy asymptotą wykresu funkcji f.
Prostą o równaniu x = a nazywamy asymptotą pionową wykresu funkcji f, jeżeli funkcja f jest określona przynajmniej z jednej strony punktu a oraz ![]()
albo ![]()
.
Jeżeli istnieją skończone granice ![]()
oraz ![]()
, to prostą o równaniu y = mx+b nazywamy asymptotą ukośną ( albo poziomą przy m = 0 ) wykresu funkcji f.
12. Badanie funkcji cd.
Schemat badania funkcji
Wyznaczamy dziedzinę funkcji
Obliczamy granice na końcach dziedziny
Wyznaczamy asymptoty wykresu funkcji
Wyznaczamy pierwszą pochodną i jej dziedzinę
Obliczamy miejsca zerowe pierwszej pochodnej
Określamy znak pierwszej pochodnej, wyznaczamy przedziały monotoniczności i ekstrema
funkcji
Wyznaczamy punkty przecięcia wykresu funkcji z osiami układu współrzędnych i wartości
funkcji w punktach wyznaczonych w 5.5, 5.6
Zbieramy wyniki z poprzednich punktów w tabeli
Szkicujemy wykres funkcji
13. Funkcja homograficzna
Funkcją homograficzną nazywamy funkcję postaci
f(x) = ![]()
gdzie c ≠ 0 i a⋅d - b⋅c ≠ 0.
Dziedziną funkcji homograficznej jest zbiór D = ![]()
.
Wykresem funkcji homograficznej jest hiperbola.
Proste o równaniach x = ![]()
oraz y = ![]()
są asymptotami tej hiperboli.
hiperbola o równaniu y = ![]()
hiperbola o równaniu y = -![]()
Aby narysować funkcję homograficzną musimy jej postać f(x) = ![]()
przekształcić do postaci f(x) = ![]()
, wtedy wykres funkcji y = ![]()
przesuwamy o wektor [ -w, t ].
Pochodna funkcji homograficznej jest równa f '(x) = ![]()
, ponieważ z założenia licznik jest różny od zera, więc pochodna funkcji nie przyjmuje wartości równej zero, czyli funkcja homograficzna nie posiada ekstremum. Znak pochodnej zależy od znaku licznika ( czyli wyrażenia a⋅d - b⋅c ). Wynika z tego, że:
funkcja homograficzna jest w przedziałach ( -∞, ![]()
) oraz ( ![]()
, +∞ ) rosnąca, gdy a⋅d - b⋅c > 0, funkcja homograficzna jest w przedziałach ( -∞, ![]()
) oraz ( ![]()
, +∞ ) malejąca, gdy a⋅d - b⋅c < 0.
14. Geometria analityczna - wektory, proste
Współrzędnymi wektora ![]()
w prostokątnym układzie współrzędnych XOY nazywamy miary jego składowych. Jeżeli punkt A( xA, yA ) jest początkiem, a punkt B( xB, yB ) jest końcem wektora ![]()
, to współrzędnymi wektora ![]()
są liczby: a = xB - xA , b = yB - yA .
Zapisujemy to symbolicznie: ![]()
[ a, b ] lub ![]()
= [ a, b ].
Jeżeli wektor ![]()
= [ a, b ], to długość wektora ![]()
wyraża się wzorem: ![]()
.
Jeżeli punkt A( xA, yA ) i punkt B( xB, yB ), to środek S odcinka ![]()
ma współrzędne:
xS =![]()
, yS = ![]()
.
Jeśli α jest miarą kąta skierowanego uporządkowanej pary niezerowych wektorów ( ![]()
, ![]()
) współrzędnych ![]()
= [ a1, a2 ], ![]()
= [b1, b2 ], to:
cos α = ![]()
, sin α = ![]()
.
Jeżeli wektory ![]()
i ![]()
mają współrzędne ![]()
= [ a1, a2 ], ![]()
= [b1, b2 ], to ich iloczyn skalarny wyraża się wzorem ![]()
⋅![]()
= a1 ⋅ b1 + a2 ⋅ b2 .
Wyznacznikiem niezerowej pary wektorów ![]()
i ![]()
o współrzędnych ![]()
= [ a1, a2 ], ![]()
= [b1, b2 ] nazywamy liczbę d( ![]()
, ![]()
) = ![]()
= a1 ⋅ b2 - a2 ⋅ b1 .
Jeżeli punkty A( xA, yA ), B( xB, yB ) i C( xC, yC ) są wierzchołkami trójkąta, to pole trójkąta ΔABC wyraża się wzorami:
P = ![]()
=![]()
=![]()
,
P = ![]()
.
Współczynnikiem kierunkowym prostej nieprostopadłej do osi OX nazywamy tangens kąta nachylenia tej prostej do osi OX.
Równaniem kierunkowym prostej l nieprostopadłej do osi OX nazywamy równanie postaci y = ax+b, gdzie a oznacza współczynnik kierunkowy prostej l, zaś b rzędną punktu, w którym l przecina oś OY.
Jeżeli punkty A( xA, yA ) i B( xB, yB ) należą do prostej l, to równanie prostej l ma postać:
y - yA = ![]()
( x - xA ), gdy xA ≠ xB , lub
( y - yA )⋅( xA - xB ) - ( yA - yB )⋅( x - xA ) = 0.
Każde równanie postaci Ax+By+C = 0, gdzie A2 +B2 ≠ 0 jest równaniem ogólnym prostej. Wektor ![]()
= [ A, B ] jest wektorem prostopadłym do tej prostej.
Odległość punktu P ( x0, y0 ) od prostej o równaniu Ax+By+C = 0 wyraża się wzorem:
d = ![]()
.
Warunki równoległości prostych
Dwie proste o równaniach y = a1 x +b1 i y = a2 x +b2 są równoległe wtedy i tylko wtedy, gdy a1 = a2.
Dwie proste o równaniach Ax+By+C = 0 i A1 x+B1 y+C1 = 0 są równoległe wtedy i tylko wtedy, gdy
AB1 - BA1 = 0.
Warunki prostopadłości prostych
Dwie proste o równaniach y = a1 x +b1 i y = a2 x +b2 są prostopadłe wtedy i tylko wtedy, gdy a1 ⋅ a2 = -1.
Dwie proste o równaniach Ax+By+C = 0 i A1 x+B1 y+C1 = 0 są prostopadłe wtedy i tylko wtedy, gdy
AA1 + BB1 = 0.
15. Geometria analityczna - krzywe stopnia drugiego
Okrąg
Równanie okręgu o środku ( a, b ) i promieniu r ma postać ( x - a )2 + ( y - b )2 = r 2 .
Równanie postaci x2 + y2 -2ax - 2by + c = 0 przedstawia okrąg wtedy i tylko wtedy, gdy a2 +b2 - c > 0, promieniem okręgu jest r = ![]()
, zaś środkiem punkt ( a, b ).
Równanie stycznej do okręgu o środku ( a, b ) i promieniu r w punkcie ( x0, y0 ) należącym do okręgu, ma postać ( x0 - a )( x - a )+( y0 - b )( y - b ) = r 2 .
Elipsa
Niech dane będą dwa punkty F1, F2 oraz liczba dodatnia a taka, że 2a > F1⋅F2 . Elipsą nazywamy zbiór tych wszystkich punktów P płaszczyzny, dla których PF1 + PF2 = 2a.
Jeśli punkty F1, F2 należą do osi OX, zaś początek układu współrzędnych jest środkiem odcinka ![]()
, to równanie elipsy ma postać ![]()
, gdzie b2 = a2 - c2 i |c| = OF1 .
Elipsa ta ma środek symetrii w punkcie ( 0, 0 ) i dwie osie symetrii proste OX i OY.
Równanie stycznej do elipsy w punkcie ( x0, y0 ) należącym do elipsy, ma postać: ![]()
.
Punkty F1, F2 nazywamy ogniskami elipsy.
Cięciwą elipsy nazywamy każdy odcinek, którego końce należą do elipsy. Średnicą elipsy nazywamy każdą cięciwę, do której należy środek symetrii elipsy. Osią wielką nazywamy najdłuższą z jej średnic. Osią małą nazywamy najkrótszą z jej średnic. Wierzchołkami elipsy nazywamy punkty wspólne elipsy i jej osi symetrii.
Mimośrodem elipsy nazywamy liczbę e = ![]()
, zaś kierownicami elipsy proste o równaniach:
x = ![]()
i x = -![]()
.
Hiperbola
Niech dane będą dwa punkty F1, F2 oraz liczba dodatnia a taka, że 2a < F1⋅F2 . Hiperbolą nazywamy zbiór tych wszystkich punktów P płaszczyzny, dla których PF1 - PF2 = 2a.
Jeśli punkty F1, F2 należą do osi OX, zaś początek układu współrzędnych jest środkiem odcinka ![]()
, to równanie hiperboli ma postać ![]()
, gdzie b2 = c2 - a2 i |c| = OF1.
Hiperbola ta ma środek symetrii w punkcie ( 0, 0 ) i dwie osie symetrii proste OX i OY.
Równanie stycznej do hiperboli w punkcie ( x0, y0 ) należącym do hiperboli, ma postać: ![]()
.
Punkty F1, F2 nazywamy ogniskami hiperboli.
Asymptotami hiperboli są elipsy proste o równaniach: y = ![]()
⋅x i y = -![]()
⋅x.
Parabola
Jest to krzywa, która w pewnym układzie XOY ma równanie y2 = 2px, gdzie p ≠ 0, 2p jest parametrem paraboli. Punkt F = ![]()
jest ogniskiem paraboli. Prosta o równaniu x = -![]()
jest kierownicą paraboli. Punkt ( 0, 0 ) jest wierzchołkiem paraboli.
Parabola jest zbiorem wszystkich punktów płaszczyzny równo odległych od jej ogniska i od jej kierownicy. Jedyną osią symetrii paraboli jest prosta OX.
Równanie stycznej do paraboli y2 = 2px w punkcie ( x0, y0 ) należącym do paraboli, ma postać:
y ⋅ y0 = p⋅ ( x + x0 ).
16. Planimetria - własności podstawowych figur planimetrycznych
Odległość punktu od prostej.
Odległość punktu od figury niepustej - długość promienia największego otoczenia kołowego tego punktu wewnątrz którego nie ma punktów tej figury. Gdy otoczenie takie nie istnieje, odległość jest zerem.
Odległość punktu od prostej równa się odległości tego punktu od jego rzutu prostokątnego na tę prostą.
Położenie prostej m względem okręgu o(A,r).
m jest styczną do o(A,r) ⇔ odl. A od m = r,
m jest sieczną o(A,r) ⇔ odl. A od m < r,
m jest zewnętrzną dla o(A,r) ⇔ odl. A od m > r.
Styczna do okręgu (tzn. prosta mająca z nim dokładnie jeden punkt wspólny) jest prostopadła do promienia łączącego punkt styczności ze środkiem okręgu.
Dwa okręgi.
Jeśli okręgi o(A,a) i o(B,b) są różne i a ≥ b, to
o(A,a) i o(B,b) są wzajemnie zewnętrzne ⇔ AB > a + b,
o(A,a) i o(B,b) są zewnętrznie styczne ⇔ AB = a + b,
o(A,a) i o(B,b) przecinają się ⇔ a - b < AB < a + b,
o(A,a) i o(B,b) są wewnętrznie styczne ⇔ a - b = AB,
o(B,b) ⊂ k(A,a) ⇔ a - b > AB.
Związki miarowe w trójkącie prostokątnym.
Jeśli ![]()
⊥![]()
i ![]()
⊥![]()
, to a2 =![]()
, sinα=![]()
, cosα=![]()
, tgα=![]()
, ctgα=![]()
, b2 =![]()
, a=![]()
=![]()
, h2 =![]()
, b=![]()
=![]()
, c2 = a2+b2 (tw. Pitagorasa), c=![]()
=![]()
.
Związki miarowe w dowolnym trójkącie.
Wzór sinusów: ![]()
, gdzie r - długość promienia okręgu opisanego na ΔABC.
Wzór cosinusów: a2 = b2 + c2 - 2bc cosα.
Symetralne wszystkich boków trójkąta przecinają się w jednym punkcie O, który jest środkiem okręgu przechodzącego przez punkty A, B, C, czyli okręgu opisanego na tym trójkącie.
Długość promienia opisanego na trójkącie r =![]()
, gdzie S jest polem trójkąta;
Dwusieczne wszystkich kątów wewnętrznych trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu stycznego do wszystkich boków trójkąta, czyli okręgu wpisanego w trójkąt.
Długość promienia okręgu wpisanego w trójkąt ![]()
, gdzie S - pole, p - połowa obwodu trójkąta.
Odcinek łączący środki dwu boków trójkąta jest równoległy do trzeciego boku i równy jego połowie.
16. Planimetria - własności podstawowych figur planimetrycznych cd.
Najważniejsze wiadomości o wielokątach.
Czworokąt - wielokąt o czterech bokach.
Suma miar kątów wewnętrznych dowolnego czworokąta jest równa 360O.
Trapez - czworokąt mający przynajmniej dwa boki równoległe.
Trapez równoramienny - trapez mający dwa boki przeciwległe nierównoległe i równe.
Jeżeli w trapezie dwa przeciwległe boki nie są równoległe, to
suma kątów wewnętrznych leżących przy każdym z tych boków jest kątem półpełnym,
odcinek łączący środki tych boków jest równoległy do podstaw (tzn. boków równoległych), a jego długość równa się połowie sumy długości obu podstaw.
W trapezie równoramiennym kąty przy każdej podstawie są przystające.
Trapez równoramienny ma jedną oś symetrii.
Czworokąt wpisany w okrąg i czworokąt opisany w kręgu.
Czworokąt wypukły można wpisać w krąg ⇔ sumy miar kątów przeciwległych w tym czworokącie są równe(każda z nich jest równa 180o).
Czworokąt wypukły można opisać na kręgu ⇔ sumy długości boków przeciwległych w tym czworokącie są równe.
Odcinki, proste i kąty w związku z okręgiem
Kąt między cięciwą i styczną
Kąt ostry między cięciwą i styczną przechodzą przez koniec cięciwy jest równy połowie kąta środkowego opowiadającego cięciwie.
Kąt środkowy i kąty wpisane oparte na tym samym łuku
Wszystkie kąty wpisane okrąg i oparte na tym samym łuku są równe każdy z nich jest równy połowie kąta środkowego opartego na tym łuku
Kąt wpisany w półokrąg (oparty na średnicy) jest prosty.
17. Rachunek prawdopodobieństwa
Kombinatoryka
Permutacje - każdy n - wyrazowy ciąg utworzony ze wszystkich elementów n elementowego zbioru. P = n!
Kombinacje - każdy k - elementowy podzbiór n - elementowego zbioru. 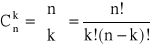
Wariacje bez powtórzeń - każdy k - wyrazowy ciąg utworzony z różnych elementów n - elementowego zbioru. ![]()
Wariacje z powtórzeniami - każdy k - wyrazowy ciąg utworzony z elementów n - elementowego zbioru. ![]()
Własności prawdopodobieństwa
P(A) ≥ 0, P(∅) = 0, P(Ω) = 1,
jeżeli A ⊂ B to P(A) ≤ P(B), dla każdego A ⊂ Ω jest P(A) ≤1,
P(A') = 1- P(A), P(A∪B) = P(A) + P(B) - P(A∩B).
Klasyczna definicja prawdopodobieństwa
Jeżeli wszystkie zdarzenia elementarne są jednakowo prawdopodobne to prawdopodobieństwo każdego zdarzenia A jest ilorazem liczby zdarzeń sprzyjających temu zdarzeniu przez liczbę wszystkich zdarzeń elementarnych. P(A) = ![]()
,
gdzie ![]()
- liczba zdarzeń sprzyjających zdarzeniu A, ![]()
- liczba wszystkich zdarzeń elementarnych.
Prawdopodobieństwo warunkowe
Prawdopodobieństwo zdarzenia A pod warunkiem zajścia zdarzenia B jest to liczba
P(A / B) = ![]()
Prawdopodobieństwo całkowite ( zupełne )
Jeśli B1, B2, ... ,Bn są zdarzeniami wyłączającymi się parami oraz ich suma jest zdarzeniem pewnym, to dla dowolnego zdarzenia A zachodzi wzór:
P(A) = P(A / B1) ⋅ P(B1) + P(A / B2) ⋅ P(B2) + ... + P(A / Bn) ⋅ P(Bn)
Niezależność zdarzeń
Zdarzenia A i B nazywamy niezależnymi, jeżeli P(A∩B) = P(A) ⋅ P(B).
W przeciwnym przypadku mówimy, że zdarzenia A i B są zależne.
Schemat Bernoulliego - ciąg powtórzeń tego samego doświadczenia
Prawdopodobieństwo otrzymania dokładnie k sukcesów w n próbach Bernoulliego wynosi:
Pn(k) = ![]()
⋅pk⋅qn-k,
gdzie p - prawdopodobieństwo sukcesu, q = 1- p - prawdopodobieństwo porażki, k = 0, 1, ... ,n.
SPIS TREŚCI
1. Zbiory. Działania na zbiorach.
22
Wyszukiwarka
Podobne podstrony:
calki wzory na egzam, Studia, Matematyka wyższa ;p
planimetria wzory, Matematyka, Liceum
Podstawowe wzory na całki, Studia, Zarządzanie, Matematyka w ekonomii i zarządzaniu
wzory matematyka finansowa
007 wzory matematyczne w Paskalu
Wzory - matematyka finansowa, Matematyka, Matematyka finansowa
Wzory matematyczne w finansach, Różne Dokumenty, MARKETING EKONOMIA ZARZĄDZANIE
Wzory Matematyczne, Prezentacje
wzory matematyczne
redagujemy wzory matematyczne
WZORY 7, Matematyka
Wzory matematyczne
wzory matematyczne lab3
wzory - matematyka finansowa, Finanse i rachunkowość, Matematyka finansowa
WZORY 8, Matematyka
Matematyka finansowa - wzory 2, Matematyka, Matematyka finansowa
METODY MATEMATYCZNE-wzory, MATEMATYKA
więcej podobnych podstron