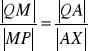Międzyszkolne Zawody Matematyczne
Klasa I LO, I Technikum
z rozszerzonym programem nauczania matematyki
Etap wojewódzki - 10.03.2007.
Czas rozwiązywania zadań: 150 minut.
Zad 1. Sporządź wykres funkcji ![]()
, a następnie zbadaj liczbę rozwiązań równania: ![]()
w zależności od parametru m.
Zad 2. Wykaż, że nie istnieją liczby naturalne x, y spełniające równanie: ![]()
.
Zad 3. Udowodnij, że jeżeli w czworokącie wypukłym dwusieczne kolejnych, sąsiednich kątów wewnętrznych przecinają się w czterech różnych punktach: K, L, M, N to sumy miar przeciwległych kątów czworokąta KLMN są równe.
Zad 4. Udowodnij, że jeśli liczby rzeczywiste a, b, c spełniają warunek ![]()
to suma pewnych dwóch spośród nich jest równa zero.
Zad 5. Punkty M i N są środkami podstaw AB i CD trapezu ABCD przy czym ![]()
. Udowodnij, że suma miar kątów: ![]()
.
Życzymy powodzenia!
Międzyszkolne Zawody Matematyczne
Klasa II LO oraz II, III Technikum
z rozszerzonym programem nauczania matematyki
Etap wojewódzki - 10.03.2007.
Czas rozwiązywania zadań: 150 minut.
Zad 1. Dana jest funkcja ![]()
. Wyznacz zbiór wartości funkcji f w zależności od parametru m.
Zad 2. Dany jest wielomian o współczynnikach całkowitych, który dla trzech różnych liczb całkowitych przyjmuje wartość 2. Wykaż, że wielomian ten dla żadnej liczby całkowitej nie przyjmuje wartości 3.
Zad 3. W trójkącie ABC o polu S poprowadzono środkową AM. Punkt K leżący na tej środkowej dzieli ją w stosunku: ![]()
. Przez punkt K i wierzchołek B poprowadzono prostą, która przecięła bok AC w punkcie D. Znajdź pole trójkąta AKD.
Zad 4. Rozwiąż równanie: 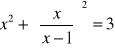
.
Zad 5. Na okręgu rozmieszczono kolejno punkty A, B, C, D. Przez każdą parę sąsiednich punktów poprowadzono okrąg. Wykaż, że punkty przecięcia się tych okręgów różne od danych leżą na jednym okręgu.
Życzymy powodzenia!
Międzyszkolne Zawody Matematyczne
Klasa III LO, IV Technikum
z rozszerzonym programem nauczania matematyki
Etap wojewódzki - 10.03.2007.
Czas rozwiązywania zadań: 150 minut.
Zad 1. Rozwiąż nierówność 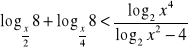
.
Zad 2. Wyznacz dziedzinę i zbiór wartości funkcji: ![]()
.
Zad 3. W czworościan foremny o krawędzi a wpisano graniastosłup trójkątny w taki sposób, że wierzchołki jego górnej podstawy są środkami ścian czworościanu. Wykonaj odpowiedni rysunek. Oblicz objętość otrzymanego graniastosłupa. Oblicz, jaką częścią objętości danego czworościanu jest objętość graniastosłupa.
Zad 4. Wykaż, że gdy n jest liczbą naturalną, to liczba ![]()
nie dzieli się przez 121.
Zad 5. Na bokach AB i AD czworokąta ABCD wpisanego w okrąg obrano takie punkty P i Q, że ![]()
oraz ![]()
. Odcinki AC i PQ przecinają się w punkcie M. Wykaż, że ![]()
.
Życzymy powodzenia!
Propozycja punktowania zadań dla poziomu pierwszego z rozszerzonym programem nauczania matematyki na etapie wojewódzkim Międzyszkolnych Zawodów Matematycznych.
Zad 1.(6 pkt.) |
||
|
Narysowanie wykresu funkcji |
2 |
|
Narysowanie w tym samym układzie współrzędnych jednego lub kilku wykresów funkcji |
2 |
|
Wyznaczenie liczby rozwiązań podanego równania w zależności od parametru m. |
2 |
Zad 2. (6 pkt.) |
||
|
Zauważenie, że dla |
2 |
|
Zauważenie, że dla |
3 |
|
Stwierdzenie, że podana suma nie przekracza liczby |
1 |
Zad 3.(6 pkt.) |
||
|
Sporządzenie odpowiedniego rysunku wraz z opisem (dla potrzeb kryteriów oznaczmy połówki kątów czworokąta ABCD przez: |
1 |
|
Zauważenie, że dwa przeciwległe spośród czterech kątów czworokąta KLMN są równe odpowiednio np: |
3 |
|
Zauważenie, że suma miar pozostałych kątów czworokąta KLMN jest równa |
2 |
Zad 4. (6 pkt.) |
||
|
Sprowadzenie do wspólnego mianownika ułamków, pomnożenie stron równania przez wspólny mianownik i dokonanie redukcji wyrażeń podobnych. |
2 |
|
Zapisanie lewej strony równania w postaci iloczynowej:
|
3 |
|
Stwierdzenie, że jeden z podanych czynników musi być równy 0 co dowodzi poprawności tezy zadania. |
1 |
Zad 5. (6 pkt.) |
||
|
Sporządzenie odpowiedniego rysunku wraz z opisem |
1 |
|
Poprowadzenie przez punkt N prostych równoległych do nierównoległych boków trapezu |
1 |
|
Zauważenie, że odcinek otrzymany w podstawie ma długość |
1 |
|
Połączenie środków ramion otrzymanego trójkąta odcinkiem o długości: |
1 |
|
Zauważenie, że otrzymany czworokąt, którego wierzchołkami są punkty M i N oraz środki ramion trójkąta ma przekątne równej długości połowiące się. Jest więc on prostokątem. |
1 |
|
Stwierdzenie, że suma miar kątów ostrych trapezu jest więc równa |
1 |
Za poprawne rozwiązanie zadanie metodą inną aniżeli opisana w schemacie punktowania należy przyznać maksymalną liczbę punktów.
Jeżeli uczeń rozwiązał zadanie inną metodą i popełnił błędy to należy określić i ocenić czynności równoważne do wymienionych w schemacie. Można przyznawać połówki punktów.
Propozycja punktowania zadań dla poziomu drugiego z rozszerzonym programem nauczania matematyki na etapie wojewódzkim Międzyszkolnych Zawodów Matematycznych.
Zad 1.(6 pkt.) |
||
|
Wymnożenie pierwszego czynnika z czwartym i drugiego z trzecim |
1 |
|
Zapisanie funkcji w postaci różnicy kwadratów:
|
2 |
|
Zauważenie, że dla każdej liczby rzeczywistej m wyróżnik trójmianu kwadratowego z pierwszego nawiasu jest nieujemny. |
1 |
|
Stwierdzenie, że najmniejsze wartość wyrażenia: |
1 |
|
Udzielenie odpowiedzi: zbiór wartości jest równy: |
1 |
Zad 2. (6 pkt.) |
||
|
Zapisanie wielomianu w postaci: |
2 |
|
Postawienie hipotezy, że istnieje liczba całkowita d taka, że |
1 |
|
Podstawienie d do wielomianu i zapisanie równania: |
1 |
|
Zauważenie, że skoro wszystkie czynniki są całkowite to dwa spośród trzech pierwszych muszą być równe i wynosić 1 lub -1. |
1 |
|
Zauważenie sprzeczności z założeniem, że liczby a, b i c są parami różne |
1 |
Zad 3.(6 pkt.) |
||
|
Narysowanie prostej równoległej do prostej BD przechodzącej przez punkt M i oznaczenie punktu wspólnego tej prostej z bokiem AC np: N |
1 |
|
Zauważenie, że: |
2 |
|
Wyznaczenie pola trójkąta AMN: |
1 |
|
Zauważenie podobieństwa trójkątów: AKD i AMN w skali |
1 |
|
Obliczenie pola trójkąta AKD: |
1 |
Zad 4. (6 pkt.) |
||
|
Skorzystanie ze wzoru: |
3 |
|
Podstawienie zmiennej
|
1 |
|
Powrót do równań ze zmienną x i rozwiązanie tych równań
dla |
1+1 |
Zad 5. (6 pkt.) |
||
|
Sporządzenie rysunku do zadania |
1 |
|
Połączenie odcinkami otrzymanych czterech punktów K, L, M, N z punktami A, B, C, D i otrzymanie czterech czworokątów: ABLK, BCML, CMND i DNKA wpisanych w okręgi. |
1 |
|
Oznaczenie kątów |
1 |
|
Zauważenie, że:
|
1 |
|
Obliczenie miar kątów: |
1 |
|
Stwierdzenie, że sumy miar kątów przeciwległych w czworokącie KLMN są równe po |
1 |
Za poprawne rozwiązanie zadanie metodą inną aniżeli opisana w schemacie punktowania należy przyznać maksymalną liczbę punktów.
Jeżeli uczeń rozwiązał zadanie inną metodą i popełnił błędy to należy określić i ocenić czynności równoważne do wymienionych w schemacie. Można przyznawać połówki punktów.
Propozycja punktowania zadań dla poziomu trzeciego z rozszerzonym programem nauczania matematyki na etapie wojewódzkim Międzyszkolnych Zawodów Matematycznych.
Zad 1.(6 pkt.) |
||
|
Wyznaczenie dziedziny nierówności: |
1 |
|
Doprowadzenie nierówności do postaci, w której za wszystkie logarytmy można wstawić nową zmienną np: |
2 |
|
Rozwiązanie nierówności wymiernej: |
2 |
|
Rozwiązanie nierówności początkowej: |
1 |
Zad 2. (6 pkt.) |
||
|
Wyznaczenie dziedziny funkcji f:
|
2 |
|
Określenie funkcji: |
2 |
|
Wyznaczenie zbioru wartości funkcji f: |
2 |
Zad 3.(6 pkt.) |
||
|
Wykonanie odpowiedniego rysunku |
1 |
|
Obliczenie długości wysokości graniastosłupa |
2 |
|
Obliczenie długości krawędzi podstawy graniastosłupa: |
1 |
|
Obliczenie objętości graniastosłupa |
1 |
|
Ustalenie zależności: |
1 |
Zad 4. (6 pkt.) |
||
|
Zapis: |
2 |
|
Rozpatrzenie przypadku, że oba składniki n+7 i n-4 różniące się o 11 dzielą się przez 11. |
2 |
|
Rozpatrzenie przypadku, że oba składniki n+7 i n-4 różniące się o 11 nie dzielą się przez 11. |
2 |
Zad 5. (6 pkt.) |
||
|
Sporządzenie rysunku wraz z oznaczeniami. |
1 |
|
Wybór takiego punktu X różnego od Q leżącego na półprostej DA, że |
1 |
|
Skorzystanie z warunku, że suma miar kątów BAD i BCD wynosi 180 stopni ( warunek okręgu opisanego na czworokącie). |
1 |
|
Obliczenie miary kąta PAX : |
1 |
|
Skorzystanie z tw. że kąty oparte na tym samym łuku wpisane w okrąg są równe : |
1 |
|
Z tw. Talesa |
1 |
Za poprawne rozwiązanie zadanie metodą inną aniżeli opisana w schemacie punktowania należy przyznać maksymalną liczbę punktów.
Jeżeli uczeń rozwiązał zadanie inną metodą i popełnił błędy to należy określić i ocenić czynności równoważne do wymienionych w schemacie. Można przyznawać połówki punktów.
Wyszukiwarka
Podobne podstrony:
mzm 2006 woj podst, Matematyka
biologia 2006 maj rozsz
chemia 2006 maj rozsz id 111803 Nieznany
1 2006 10 09 matematyka finansowaid 8919
2006.03.20 matematyka finansowa
2006 06 05 matematyka finansowaid 25460
efs-5-RPRDz-2-6-2006-woj-lodzkie , Fundusze Unijne
modzel, Pytania egzaminacyjne z Matematyki Dyskretnej z 2006 r., Pytania egzaminacyjne z Matematyki
1 2006.10.09 matematyka finansowa
mzm - etap wojewodzki 2005, Matematyka
biologia 2006 maj rozsz
chemia 2006 maj rozsz
więcej podobnych podstron