![]()
WSTĘP TEORETYCZNY:
Bryłą sztywną nazywamy ciało stałe, które nie deformuje się pod wpływem działania sił zewnętrznych. Ruch bryły można rozłożyć na ruch postępowy jej środka masy oraz ruch obrotowy.
Moment bezwładności bryły sztywnej:
jest sumą stałej wielkości Jo (na nią składają się momenty bezwładności pręta i każdego z ciężarków oraz bloku, na którym zwinięta jest nić) oraz momentu bezwładności obu kul względem osi całego układu:
![]()
(twierdzenie Steinera)
Dynamika ruchu obrotowego oraz opadającego ciężarka:
schemat układu doświadczalnego:
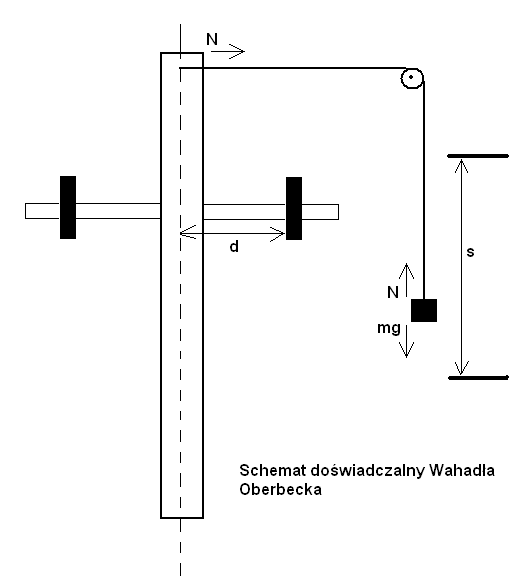
Na ciężarek działa siła ciężkości (m∙g) oraz przeciwnie zwrócona siła naciągu nici o wartości N.
Zgodnie z równaniem Newtona ciężarek opada ruchem jednostajnie przyspieszonym prostoliniowym:
![]()
Siła naciągu nici działając na bryłę wahadła o momencie bezwładności J wytwarza moment siły P o wartości:
![]()
gdzie:
r - promień walca, czyli ramię działającej siły.
Ten moment siły powoduje jednostajnie przyspieszony ruch wahadła Oberbecka z przyspieszeniem kątowym ε spełniającym równanie Newtona ruchu obrotowego:
![]()
Zatem ruch jednostajnie przyspieszony ciężarka i wahadła, ciał związanych ze sobą nicią, opisać można za pomocą poniższego układu równań:
![]()
Z powyższego układu równań wynika: ![]()
Za wzoru ![]()
wynika ![]()
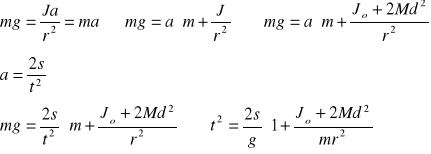
Zależność t2(d2)
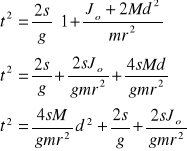
Zależność t2(s)
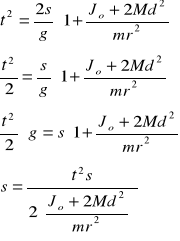
PLAN PRACY:
Zapoznanie się z działaniem fotokomórek, sprawdzenie jednostki, w której wskazywany jest czas.
Zmierzenie suwmiarką promienia r walca wahadła Oberbecka.
Odpowiedni dobór jednostek: s, d, M, m.
Wykonanie serii pomiarów czasu t opadania ciężarka dla co pięciu odległości s. Pomiar czasu dla każdej drogi powtarzamy trzykrotnie.
Dla ustalonej drogi s wykonanie serii pomiarów t opadania tego ciężarka m dla pięciu różnych odległości d ciężarka M zamocowanego na ramieniu wahadła.
OBLICZENIA ORAZ RACHUNEK NIEPEWNOŚCI POMIAROWEJ:
Poniżej zestawiono wstępne pomiary potrzebne przy obliczeniach, których dokonano przez przystąpieniem do właściwej pracy:
M = 0,125 kg
m = 0,1 kg
2d1 = 0,593 m
2d2 = 0,574 m
r = 0,01 m
Dane uzyskane podczas sprawdzania zależności drogi przebytej przez ciężarek od kwadratu czasu potrzebnego na przebycie tej drogi zamieszczono w poniższej tabeli:
Numer pomiaru |
s1 [m] |
s2 [m] |
|
t1 [s] |
t2 [s] |
t3 [s] |
|
t2 [s2] |
1 |
0,152 |
0,117 |
0,135 |
8,035 |
8,115 |
7,962 |
8,037 |
64,599 |
2 |
0,275 |
0,236 |
0,256 |
11,095 |
11,152 |
11,429 |
11,225 |
126,008 |
3 |
0,380 |
0,340 |
0,360 |
13,260 |
13,074 |
13,489 |
13,274 |
176,208 |
4 |
0,493 |
0,473 |
0,483 |
15,909 |
15,702 |
15,739 |
15,783 |
249,114 |
5 |
0,762 |
0,720 |
0,741 |
19,240 |
19,499 |
19,359 |
19,366 |
375,042 |
Wartość ![]()
obliczono ze wzoru:
![]()
dla każdego z pomiarów. Poniżej przedstawiono przykładowe obliczenia:
![]()
Z obliczaniem wartości ![]()
związane są następujące niepewności pomiarowe:
systematyczna ± 0,001, ponieważ taka jest skala przyrządu, którym mierzono odległości pomiędzy fotokomórkami.
wynikająca ze wzoru: ![]()
numer pomiaru |
s1 |
s2 |
|
Δ |
1 |
0,152 |
0,117 |
0,135 |
0,0088 |
2 |
0,275 |
0,236 |
0,256 |
0,0098 |
3 |
0,380 |
0,340 |
0,360 |
0,010 |
4 |
0,493 |
0,473 |
0,483 |
0,005 |
5 |
0,762 |
0,720 |
0,741 |
0,011 |
Przykładowe obliczenia:
![]()
Wartość ![]()
obliczono ze wzoru:
![]()
dla każdego pomiaru. Poniżej przedstawiono przykładowe obliczenia:
![]()
Niepewność pomiarową ![]()
, związaną z pomiarem czasu, wyliczono z poniższego wzoru:
![]()
numer pomiaru |
|
|
|
Σ |
Δt [s] |
1 |
0,002 |
0,078 |
0,075 |
0,155 |
0,052 |
2 |
0,130 |
0,073 |
0,204 |
0,407 |
0,136 |
3 |
0,014 |
0,200 |
0,215 |
0,429 |
0,143 |
4 |
0,126 |
0,081 |
0,044 |
0,251 |
0,084 |
5 |
0,126 |
0,133 |
0,007 |
0,266 |
0,089 |
Przykładowe obliczenia:
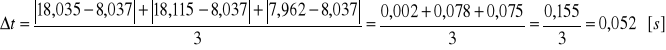
Zatem niepewność Δt2 określono wzorem:
![]()
Numer pomiaru |
|
|
|
1 |
65,434 |
63,769 |
0,832 |
2 |
129,075 |
122,978 |
3,048 |
3 |
180,028 |
172,429 |
3,799 |
4 |
251,765 |
246,476 |
2,645 |
5 |
378,484 |
371,616 |
3,434 |
Dane potrzebne do potwierdzenia zależności kwadratu odległości obciążników zamontowanych na wahadle od kwadratu czasu potrzebnego na przebycie określonej drogi zamieszono poniżej:
S = (0,229+0,269)/2 = 0,249 [m]
|
2d1 |
2d2 |
|
d2 |
Δd |
Δd2 |
t1 |
t2 |
t3 |
|
t2 |
Δt |
Δt2 |
1 |
0,593 |
0,574 |
0,292 |
0,085 |
0,002 |
0,001 |
10,454 |
10,658 |
10,819 |
10,644 |
113,288 |
0,126 |
2,692 |
2 |
0,513 |
0,493 |
0,252 |
0,063 |
0,003 |
0,001 |
9,754 |
9,294 |
9,615 |
9,554 |
91,285 |
0,174 |
3,316 |
3 |
0,433 |
0,414 |
0,212 |
0,045 |
0,002 |
0,001 |
8,581 |
8,307 |
8,107 |
8,332 |
69,417 |
0,166 |
2,770 |
4 |
0,352 |
0,333 |
0,171 |
0,029 |
0,002 |
0,001 |
7,072 |
7,355 |
7,202 |
7,210 |
51,979 |
0,097 |
1,397 |
5 |
0,271 |
0,251 |
0,131 |
0,017 |
0,003 |
0,001 |
6,404 |
6,274 |
6,154 |
6,277 |
39,405 |
0,084 |
1,060 |
Do obliczenia danych zawartych w tabeli posłużono się poniższymi wzorami:
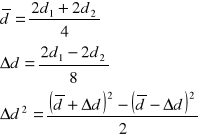
Wartości dla czasu wyznaczono w ten sam sposób jak przy określaniu poprzedniej zależności- t2(s).
Następnie dla badanych relacji t2(s) oraz t2(d2) wykonano wykresy i dopasowano zależność liniową wyznaczając współczynnik korelacji:
zależność t2(s):
Zależność t2(d2):
Wyprowadzony wcześniej wzór na zależność t2(d2) ma postać:
![]()
co możemy zapisać: ![]()
Z regresji liniowej otrzymano wzór: y = 1099,2 x + 20,409 , gdzie x = d2.
Zatem równanie na moment bezwładności będzie miało postać:
![]()
P O P R A W A
Wyprowadzony wzór:
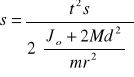
przedstawia zależność s(t2) a nie zależność t2(s) jak zapisano poprzednio.
Po obliczeniu wzoru: y = 504,9x przeprowadzano obliczenia związane z wyznaczaniem momentu bezwładności Jo z wykresu prostej t2(s):
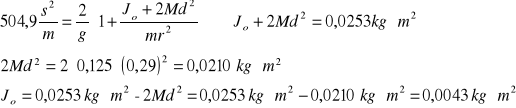
Po wyprowadzeniu wzoru na zależność t2(d2):
![]()
Za wyrażenia ![]()
podstawiono kolejno współczynniki A i B obliczone przy wyznaczaniu regresji liniowej.
|
współczynnik A |
współczynnik B |
doświadczalnie |
1099,2 |
20,409 |
teoretyczne |
|
|
Różnica pomiędzy współczynnikami A i B wyznaczonymi doświadczalnie i teoretycznie odbiegają od siebie. Szczególnie w przypadku współczynnika A. Wynikają one z błędów pomiarów oraz niedokładności przy wykonywaniu doświadczenia- złego ustawienia fotokomórki czy zatrzymywaniu stopera oraz mierzeniu odległości. Wszystkie te czynniki wpływają na owe różnice.