KIERUNEK Mechatronika
Realizowany w ramach projektu „Politechnika XXI wieku” współfinansowanego ze
środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
ĆWICZENIE NR 5
Porównanie niedokładności pomiarów wielkości kątowych metodami pośrednimi
Projekt Politechnika XXI wieku współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego;
Nr umowy UDA-POKL.04.01.01-00-121/09
Porównywanie niedokładności pomiarów wielkości kątowych metodami pośrednimi
Każdy pomiar charakteryzuje się określoną niedokładnością lub niepewnością w skutek oddziaływania na przebieg pomiaru różnego rodzaju czynników, zarówno o charakterze systematycznym jak i przypadkowym. W bezpośrednich metodach pomiaru czynniki systematyczne można bardzo łatwo zdefiniować, ponieważ ich wpływ na wynik pomiaru jest bezpośredni o charakterze stałym lub zmiennym liniowo zależnym od wartości mierzonej.
W technice wykonuje się szereg pomiarów różnych wielkości stosując często pośrednie metody pomiaru. W technice budowy maszyn pośrednie metody pomiaru stosuje się często do pomiaru wielkości kątowych (z systemu wielkości i jednostek miar SI wynika, że wielkość kątową może być definiowana jako wielkość pochodna długości z wyrażeniem jej wartości radianach). Metody pośrednie pozwalają definiować kąt jako wielkość pochodną długości oraz zapewniają możliwość realizacji dokładnych pomiarów wartości kątowych przyrządami do pomiaru długości o niekoniecznie wysokiej dokładności. Często są jedynymi metodami umożliwiającymi wykonanie pomiaru z uwagi na brak możliwości dostępu do danego wymiaru kątowego.
W pośrednich metodach pomiaru, niedokładność pomiaru zależy nieliniowo od wartości mierzonej. Z tego względu praktyczne wyznaczenie niedokładności pomiaru jest bardziej złożone niż w metodach bezpośrednich. Należy zwrócić uwagę, że w pomiarach pośrednich wpływ wielkości mierzonych bezpośrednio na niedokładność pomiaru wielkości mierzonej pośrednio jest zróżnicowany i zależy od rodzaju funkcji wiążącej mierzone wielkości.
Przebieg ćwiczenia
Przed przystąpieniem do pomiarów należy sprawdzić wyposażenie stanowiska laboratoryjnego do pomiaru kątów w przyrządy, wzorce i pomoce pomiarowe.
Następnie należy sprawdzić wartość wskazania zerowego przyrządów przeznaczonych do pomiarów bezpośrednich (głębokościomierza, mikromierza, kątomierza, kątomierza poziomicowego). Jeżeli występują błędy wskazania zerowego należy odczytać ich wartości i uwzględnić je jako poprawki. Wartość wskazania zerowego dla kątomierzy należy wyznaczyć w następujący sposób;
dla kątomierza uniwersalnego jako wzorca wartości zerowej kąta użyć płaszczyzny płyty pomiarowej przykładając do niej powierzchnie pomiarowe ramion kątomierza uniwersalnego i odczytując wskazanie zerowe,
dla kątomierza poziomicowego należy ustawić go na powierzchni płyty pomiarowej w miejscu w którym będzie wykonywany pomiar i dokonać pomiaru jej pochylenia odczytując wartość względną wskazania,
Wykonać pomiary wstępne danego kąta przy pomocy kątomierza uniwersalnego i kątomierza poziomicowego i wykonać pomiary zbieżności/pochylenia przy pomocy suwmiarki zgonie ze szkicem na rys.1.
Wyznaczyć wartości wstępnego pomiaru zbieżności/pochylenia według wzorów (1,2), zbieżność
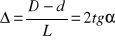
(1)Wyznaczyć wartość wstępną stosu płytek wzorcowych Hwst ze wzoru (3).
Wykonać pomiary kąta z użyciem liniału sinusowego. W tym celu należy:
Wykonać pomiary zbieżności/pochylenia dla kąta zewnętrznego z użyciem wałeczków pomiarowych. W tym celu należy:
Wykonać pomiary kąta wewnętrznego z użyciem kulek pomiarowych. W tym celu należy:
Wyznaczyć niedokładności pomiarów wartości kąta lub zbieżności/pochylenia stosownie do opisanej w pkt 6.4. metody pomiarowej [1],
Sprawdzić czy występuje zgodność wartości wyników pomiarów dla dwóch metod. Jeżeli wartości wyników pomiarów są zgodne, to powinny być spełnione warunki;
Jeżeli żaden z warunków nie jest spełniony oznacza to nieprawidłowo wykonany pomiar.
pochylenie ![]()
(2)
Rys. 1. Zasada pomiaru wstępnego kąta/zbieżności/pochylenia poprzez pomiar
wymiarów długości
![]()
(3)
a na podstawie wyników wstępnego pomiaru kąta lub zbieżności/pochylenia dobrać przyrządy pomiarowe o odpowiednich zakresach pomiarowych, oraz średnice kulek pomiarowych dla stożka wewnętrznego.
- przygotować stanowisko do pomiarów zgodnie z rys.2. Pomiar polega na takim dobraniu wysokości stosu płytek HS, aby różnica wskazań czujnika ΔW była równa
![]()
(4)
- dobieranie stosu płytek HS rozpocząć od wcześniej wyznaczonej wartości wstępnej Hwst
- wartość mierzonego kąta α należy wyznaczyć z zależności:
![]()
(5)
- w przypadku, gdy wskazania czujnika 3 są różne ΔW =W1 - W2 ≠ 0 należy obliczyć poprawkę c wysokości stosu płytek z proporcji przedstawionych na rys.3.
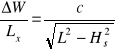
(6)
![]()
(7)
a wartość mierzonego kąta należy wtedy wyznaczyć z zależności:
![]()
(8)
Przy obliczaniu poprawki c należy zwrócić uwagę na jej znak algebraiczny tzn. jeżeli wskazanie czujnika przesuwanego od położenia W1 do W2 maleje (W1 > W2) to poprawka ma znak minus, gdy W1 < W2 poprawka ma znak plus.
Rys. 2. Zasada pomiaru kąta przy pomocy liniału sinusowego:
1- liniał sinusowy, 2 - stos płytek wzorcowych, 3 - czujnik, 4 - statyw czujnika, 5 - mierzony przedmiot, L - rozstaw wałeczków liniału równy 100mm lub 200mm
Rys. 3. Schemat pomocniczy do wyznaczenia poprawki c
- ustawić mierzony przedmiot na płycie pomiarowej lub stoliku przyrządu pomiarowego (np. długościomierza).
- zestawić dwa jednakowe stosy płytek wzorcowych o wymiarze H1 ≈ 5÷10 mm, oraz dobrać dwa jednakowe wałeczki pomiarowe o średnicy dw≈ 5 mm,
- dokonać pomiaru wymiaru M1 rys.4,
- zestawić dwa stosy płytek wzorcowych o wartościach H2 możliwie największych.
- dokonać pomiaru wymiaru M2 rys.4,
- zbieżność Δ powierzchni stożkowej należy wyznaczyć z zależności
![]()
(9)
Rys.4. Pomiar zbieżności stożka zewnętrznego: 1 - wałeczki pomiarowe o średnicy dw,
2 - stosy płytek wzorcowych, 3 - mierzony stożek
- pochylenie Λ powierzchni stożkowej należy wyznaczyć z zależności
![]()
(10)
Pomiary wymiarów M1 i M2 można wykonać metodą bezpośrednią przy pomocy mikromierza klasycznego lub cyfrowego. Gdy wymagana jest wysoka dokładność, pomiary można wykonywać nawet przy pomocy długościomierza Abbego. Wybór przyrządu do pomiaru wymiarów M1 i M2 zależy od wymaganej dokładności pomiaru.
Przy pomiarze zbieżności stożka z użyciem wałeczków pomiarowych należy zwrócić uwagę, że nacisk pomiarowy wywołuje siłę osiową Fv, która może w czasie pomiaru przemieścić mierzony przedmiot a tym samym spowodować błąd pomiaru wymiarów Mi.
- dobrać dwie kulki pomiarowe o średnicach d1 i d2 spełniających warunki
![]()
i ![]()
- wykonaniu pomiarów wymiarów H1 i H2.
- wartość mierzonego kąta α stożka należy wyznaczyć ze wzoru
![]()
(11)
- zbieżność stożka Δ należy wyznaczyć z zależności:
![]()
(12)
lub ze wzoru przybliżonego (dla małych zbieżności)
![]()
![]()
(13)
Rys. 5. Zasada pomiaru kąta stożka wewnętrznego z użyciem kulek pomiarowych:
1- stosy płytek wzorcowych, 2- kulki pomiarowe o średnicach d1 i d2,
3- mierzony przedmiot
W praktyce dokładność pomiaru tą metodą znacznie może odbiegać od obliczonej dokładności teoretycznej, z uwagi na możliwość wystąpienia zbyt dużego nacisku pomiarowego. Nacisk pomiarowy na styku kulka-powierzchnia stożka rośnie, gdy kąt rozwarcia mierzonego stożka maleje. Zbyt duży nacisk pomiarowy może wystąpić szczególnie przy pomiarach stożków wewnętrznych o małym kącie rozwarcia np. stożków Morse'a. Wpływ nacisku pomiarowego na praktycznie uzyskiwaną dokładność pomiaru będzie mało istotny, jeżeli zostaną spełnione warunek
![]()
(14)
- dla kąta
![]()
- dla zbieżności/pochylenia
![]()
gdzie: wskaźnik 1 odnosi się do jednej metody pomiaru kąta/zbieżności,
wskaźnik 2 odnosi się do drugiej metody pomiaru tego samego kąta.
Zalecana literatura
Podstawowa:
1. Kujan K.: Technika i systemy pomiarowe w budowie maszyn laboratorium. WPL, (2004).
Uzupełniająca:
2. Jakubiec W. Malinowski J.: Metrologia wielkości geometrycznych. WNT 1993, 1999.
1
d2
d1
ld
W1
W2
Lx
α
HS
L
3
4
1
α
5
2
W1
W2
c
ΔW
Lx
![]()
H1
H2
H =H2 - H1
M1
M2
M=M2-M1
α
1
3
2
2
1
F
dw
H1
H2
L
1
2
3
H
α
d2
d1
Dmax
Dmin
2
Wyszukiwarka
Podobne podstrony:
Mechatronika ćw 8, I,II, I, MET, geometryczna, LAB, INSTR
Mechatronika ćw 1, I,II, I, MET, geometryczna, LAB, INSTR
Mechatronika ćw 6, I,II, I, MET, geometryczna, LAB, INSTR
Mechatronika ćw 3, I,II, I, MET, geometryczna, LAB, INSTR
Mechatronika ćw 7, I,II, I, MET, geometryczna, LAB, INSTR
Wyka z ćwicz. BHP i reg.2012, I,II, I, MET, geometryczna, LAB, INSTR
druk, I,II, I, MET, geometryczna, LAB, INSTR
cw.2, II Rok, Elektrotechnika-lab
Wnioskicw4, Mechatronika, Rok II, Semestr III, Elektronika, Lab
Opracowanie koducw4 (1), Mechatronika, Rok II, Semestr III, Elektronika, Lab
open colector, Mechatronika, Rok II, Semestr III, Elektronika, Lab
cw.16, II Rok, Elektrotechnika-lab
Ćw 6 El, PW Transport, II rok, Elektrotechnika 3 lab, Cykl 2 opracowane zagadnienia
elektro7, Mechatronika, Rok II, Semestr III, Elektronika, Lab
APT LAB instr 5
Sprawko - ćw 6a, Politechnika Poznańska, Lab. Pomiary Wielkości Mechanicznych
instrukcja cw 1, II rok, II semestr, Chemia wody i powietrza
Przetwórstwo opracowane pytania MZ 2B DZ (1), Mechatronika, Rok II, Semestr III, PTS i skrawanie
ćw II
więcej podobnych podstron