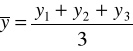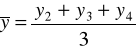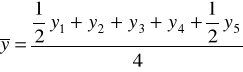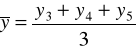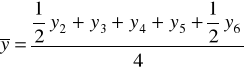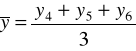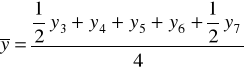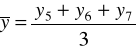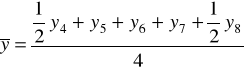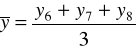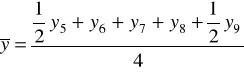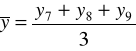Składnikowa analiza szeregów czasowych
W szeregach czasowych wyróżnia się tradycyjnie dwie składowe:
składowa systematyczna. Jest ona efektem oddziaływania na badane zjawisko tzw. przyczyn głównych
składowa przypadkowa (losowa). Jest efektem działania przyczyn ubocznych, tj. nieistotnych dla „normalnego” przebiegu badanego zjawiska.
Składowa systematyczna może wystąpić w różnych postaciach, a mianowicie:
1. trendu,
2. stałego przeciętnego poziomu badanego zjawiska (gdy trend nie występuje),
3. wahań cyklicznych,
4. wahań sezonowych.
Najczęściej przez trend rozumie się dążność badanego zjawiska do wzrostu bądź spadku, przejawiającą się w dłuższym przedziale czasowym (w odpowiednio długim czasie).
Stały (przeciętny) poziom zjawiska występuje wówczas, gdy jego wartości oscylują wokół pewnego stałego poziomu. Mówimy o nim wtedy, gdy w szeregu czasowym nie ma tendencji rozwojowej.
Wahania cykliczne − długookresowe rytmiczne wahania badanego zjawiska wokół trendu, następujące w sposób regularny i cykliczny, np. wahania koniunkturalne.
Wahania sezonowe − wahania poziomu badanego zjawiska wokół tendencji rozwojowej, następujące w cyklu rocznym. Wahania te związane są z następstwem pór roku.
Proces wyodrębniania poszczególnych składowych szeregu czasowego określa się mianem dekompozycji szeregu czasowego.
Najczęściej przy tym, identyfikacji poszczególnych składowych szeregu czasowego dokonuje się na podstawie analizy graficznej.
Wyróżnia się z reguły dwa podstawowe modele szeregów czasowych:
Model addytywny − zakłada się w nim, że obserwowane zjawiska są sumą składowych szeregu czasowego. Można to wyrazić relacją:
![]()
,
gdzie:
− trend
− wahanie cykliczne
− wahanie sezonowe
− wahania przypadkowe
t − zmienna czasowa
W modelu tym zakłada się więc, że poszczególne składowe są efektem działania innych przyczyn − nie ma więc interakcji między nimi.
Model multiplikatywny − przyjmuje się w nim, że obserwowane wartości badanego zjawiska są iloczynem składowych szeregu czasowego.
Mamy więc w tym przypadku relację:
![]()
W modelu tym składowe mogą wchodzić ze sobą w interakcje, jako że są pod wpływem działania takiego samego splotu przyczyn (oczywiście nie muszą to być wszystkie takie same przyczyny).
Model multiplikatywny jest najczęściej wykorzystywany w praktyce. W modelu tym trend jest wyrażany w jednostkach mianowanych takich, jak badane zjawisko, wahania natomiast są określane jako względne odchylenia od tendencji rozwojowej.
Proces dekompozycji szeregu czasowego może odbywać się w sposób:
klasyczny − polegający na sekwencyjnym wyodrębnianiu poszczególnych składowych szeregu czasowego,
integralny − zakładający jednoczesną estymację składowych szeregu czasowego.
Wyrównywanie szeregów czasowych - wyodrębnianie tendencji rozwojowej (trendu)
Można wyróżnić dwie podstawowe metody wyrównywania szeregów czasowych:
metodę mechaniczną,
metodę analityczną.
Metoda mechaniczna polega na opisie rozwoju zjawiska w czasie za pomocą tzw. średnich ruchomych, których wartości traktujemy jako wartości trendu.
Średnia ruchoma jest to średnia arytmetyczna obliczona z pewnej liczby k-kolejnych wyrazów szeregu czasowego.
Liczba k określana jest mianem stałej wygładzania. Wraz ze wzrostem stałej wygładzania rośnie efekt wyrównania, co oznacza, że szereg czasowy jest lepiej wygładzony.
Z drugiej strony wzrost liczby k powoduje większe skrócenie szeregu czasowego.
Jeśli stała wygładzania jest liczbą nieparzystą, to szereg wyjściowy jest skrócony o ![]()
okresy początkowe i końcowe.
Jeśli natomiast stała wygładzania jest liczbą parzystą, to szereg wyjściowy jest skrócony o ![]()
okresy początkowe i końcowe.
Wybór liczby wyrazów średniej ruchomej musi więc stanowić kompromis. Sugeruje się w związku z powyższym, by przy wyborze liczby k spełniony był warunek:
![]()
W praktyce zaleca się, jeśli w szeregu czasowym występuje tylko trend, stosowanie średniej ruchomej z nieparzystej liczby wyrazów.
Wtedy następuje przyporządkowanie obliczonej średniej okresowi środkowemu.
Jeśli natomiast w szeregu czasowym występują obok trendu również wahania sezonowe (okresowe), to stała wygładzania powinna liczyć tyle wyrazów, ile podokresów sezonowych występuje w cyklu wahań (jeśli np. występują kwartalne wahania sezonowe to k=4 ).
Średnią ruchomą obliczaną z parzystej liczby wyrazów nazywa się średnią ruchomą scentrowaną.
Metodę mechaniczną, czyli sposób liczenia średnich ruchomych trzy- i cztero-okresowych zaprezentowano w tabeli.
Metoda mechaniczna
Lata |
Poziom zjawiska - yt |
Średnie ruchome 3 - okresowe |
Średnie ruchome 4 - okresowe |
1998
|
y1 |
- |
- |
1999 |
y2 |
|
- |
2000 |
y3 |
|
|
2001 |
y4 |
|
|
2002 |
y5 |
|
|
2003 |
y6 |
|
|
2004 |
y7 |
|
|
2005 |
y8 |
|
- |
2006
|
y9 |
- |
- |
Przykłady
Zadanie 1.
Zbiory ziemniaków w pewnej gminie w Polsce w latach 1998-2006 przedstawiały się następująco:
Lata |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
Zbiory w tys. t |
36,3 |
29,0 |
23,4 |
36,3 |
23,1 |
24,9 |
27,2 |
20,8 |
25,9 |
Wyznacz tendencję rozwojową zbiorów ziemniaków w Polsce w badanych latach stosując metodę mechaniczną.
Rozwiązanie:
Liczymy średnią ruchomą 3-letnią i sporządzamy wykres szeregu wyjściowego
i średnich ruchomych:
Lata |
Zbiory w mln ton |
Obliczenia |
Średnia 3-letnia |
1990 |
36,3 |
- |
- |
1991 |
29,0 |
(36,3+29,0+23,4)/3 |
29,57 |
1992 |
23,4 |
(29,0+23,4+36,3)/3 |
29,57 |
1993 |
36,3 |
(23,4+36,3+23,1)/3 |
27,60 |
1994 |
23,1 |
(36,3+23,1+24,9)/3 |
28,10 |
1995 |
24,9 |
(23,1+24,9+27,2)/3 |
25,07 |
1996 |
27,2 |
(24,9+27,2+20,8)/3 |
24,30 |
1997 |
20,8 |
(27,2+20,8+25,9)/3 |
24,63 |
1998 |
25,9 |
- |
- |
Wniosek: Zbiory ziemniaków w Polsce w badanych latach charakteryzowały się zmienną tendencją. Wyliczone średnie ruchome wskazują jednak na ich spadkowy trend rozwojowy.
Metoda analityczna − jej istota sprowadza się do przyjęcia założenia, że zmiany zjawiska w czasie można przedstawić jako funkcję zmiennej czasowej z dokładnością do składnika losowego.
Oznacza to budowę modelu szeregu czasowego, w którym jedyną zmienną objaśniającą jest zmienna czasowa.
Zmienna ta, rzecz jasna, nie jest bezpośrednią przyczyną zmian zachodzących w rozwoju badanego zjawiska, stanowi ona natomiast wypadkową wpływu czynników, które te zmiany powodują.
Zmienna czasowa t jest to zmienna, której realizacje będące kolejnymi liczbami całkowitymi, przyporządkowane są poszczególnym jednostkom czasowym według zasady następstwa czasowego.
Najczęściej przyjmuje się przy tym, że realizacje zmiennej czasowej są liczbami naturalnymi i przyjmują wartości:
t = 1, 2, 3, ... , n
n − liczba obserwacji w szeregu czasowym.
Model trendu jest to więc konstrukcja formalna, za pomocą której przedstawia się przebieg badanego zjawiska w czasie. W modelu tym zmienną objaśniającą (jedyną) jest zmienna czasowa, która reprezentuje upływ czasu syntetyzując wpływ bliżej nieznanych czynników na zachowanie się rozpatrywanego w czasie zjawiska.
W rezultacie zapis formalny modelu trendu ma postać:
![]()
t = 1, 2, 3, ..., n
gdzie:
f(t) − funkcja trendu,
− składnik losowy.
Składnik losowy charakteryzuje efekty oddziaływania na badane zjawisko wahań przypadkowych. Zakłada się przy tym, że jego wartość oczekiwana wynosi zero, natomiast wariancja jest skończona.
Podstawowym problemem w metodzie analitycznej jest określenie postaci analitycznej f(t). Przy jej wyborze kierujemy się zwykle następującymi przesłankami:
Wybrana funkcja powinna być prosta analitycznie.
Parametry strukturalne funkcji powinny być interpretowalne.
Należy wybierać funkcje, których parametry można estymować klasyczną metodą najmniejszych kwadratów.
Wybrana funkcja powinna być zgodna z empirycznymi wynikami badań.
Powyższe przesłanki powodują, że najczęściej wykorzystywanymi w praktyce empirycznej funkcjami są:
funkcja liniowa
![]()
(1)
funkcja paraboliczna
![]()
(2)
funkcja potęgowa
![]()
(3)
funkcja wykładnicza
![]()
(4)
funkcja hiperboliczna
![]()
(5)
funkcja logistyczna
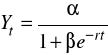
(6)
Wszystkie wymienione funkcje (2−6) można sprowadzić, po dokonaniu pewnych transformacji, do postaci liniowej.
W związku z powyższym nasze dalsze rozważania poświęcimy estymacji liniowej funkcji trendu.
Załóżmy więc, że funkcja trendu ma postać:
![]()
,
gdzie:
yt − poziom badanego zjawiska w jednostce czasu t,
t − zmienna czasowa (t = 1, 2, …, n),
ut − realizacje składnika losowego,
![]()
− parametry liniowej funkcji trendu.
Parametr 1 określa, jaki jest przeciętny okresowy przyrost badanej zmiennej Y w analizowanym przedziale czasowym, zaś parametr 0 wskazuje na teoretyczny poziom tej zmiennej w tym okresie, dla którego t = 0.
Parametry ![]()
szacuje się stosując klasyczną metodę najmniejszych kwadratów, otrzymując ich oceny w postaci:
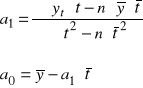
,
gdzie:
![]()
− średnia arytmetyczna zmiennej Y w przedziale czasowym <1, n>,
![]()
− średnia arytmetyczna zmiennej czasowej,
![]()
− realizacje zmiennej Y w okresie t (t = 1, 2, …, n).
Po oszacowaniu parametrów strukturalnych funkcji trendu konieczna jest ocena jej jakości. Ocena ta dokonywana jest ze względu na następujące kryteria:
Kryterium błędu losowego
Obliczamy wtedy:
odchylenie standardowe składnika losowego (resztowego)
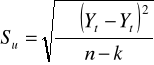
gdzie:
![]()
− wartości empiryczne zmiennej ( t = 1, 2, 3, ..., n ),
![]()
− wartości teoretyczne ( wartości trendu ) zmiennej objaśnianej,
k − liczba szacowanych parametrów trendu.
Parametr ![]()
mówi, jaki przeciętnie biorąc, popełniamy błąd szacując poziom badanego zjawiska na podstawie funkcji trendu.
współczynnik zmienności losowej:
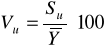
gdzie:
![]()
− średnia arytmetyczna zmiennej objaśnianej.
Miara ta określa, jaki procent średniego poziomu badanego zjawiska stanowi odchylenie standardowe składnika resztowego.
Z reguły przyjmuje się, że jeżeli:
![]()
,
to błąd losowy modelu trendu można uznać za relatywnie mały i w konsekwencji ocenić model za dopuszczalny z punktu widzenia tego kryterium.
Kryterium dokładności opisu badanego wycinka rzeczywistości (badanego zjawiska)
Obliczamy wtedy:
współczynnik zgodności:
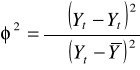
Miernik ten przyjmuje wartości z przedziału ![]()
i określa, jaką część badanego zjawiska nie opisuje wybrana funkcja trendu. Im ![]()
, tym jakość (dokładność) opisu trendu przez zastosowaną funkcję jest lepsza.
współczynnik determinacji:
![]()
Miara ta, rzecz jasna, również przyjmuje wartość z przedziału ![]()
i określa, jaka część zmienności badanego zjawiska jest wyjaśniona przez funkcję trendu.
Łatwo zauważyć, że im ![]()
, tym model trendu jest lepszy, czyli tym dokładność opisu zachowania się badanej zmiennej w czasie, przez zastosowaną funkcję trendu jest lepsza.
Umownie przyjmuje się często, że jeśli ![]()
, to model trendu jest dopuszczalny z punktu widzenia tego kryterium.
Warto jednak zaznaczyć, że o przyjętej normie granicznej decyduje podmiot badający.
Kryterium precyzji szacunku parametrów modelu trendu.
W tym celu oblicza się błędy średnie szacunku ocen parametrów funkcji trendu, a następnie porównuje się je z tymi ocenami. Jeśli otrzymana relacja (umownie biorąc) jest większa od 2 to można uznać, że dany parametr funkcji trendu został oszacowany precyzyjnie.
Jeśli funkcja trendu jest liniowa to błędy średnie szacunku ocen parametrów dane są wzorami:
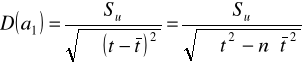
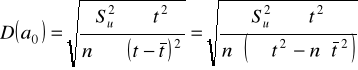
Oceny parametrów trendu liniowego uznamy za precyzyjne, jeśli (jak już zaznaczyliśmy wcześniej):
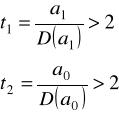
Oszacowaną funkcję trendu można następnie wykorzystać do sporządzenia prognozy. Prognozę zmiennej Y na okres T otrzymuje się przez ekstrapolację funkcji trendu, czyli przez podstawienie do modelu w miejsce zmiennej czasowej t jej realizacji właściwej dla okresu prognozowanego T. Załóżmy, że realizacja ta wynosi tT. Wtedy:
![]()
czyli w przypadku liniowej funkcji trendu:
![]()
.
Tak skonstruowana prognoza jest prognozą punktową. Ocena jej jakości dokonywana jest przez obliczenie średniego błędu prognozy ex ante według wzoru:
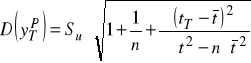
oraz względnego błędu prognozy ex ante według relacji:
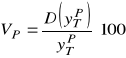
.
Z reguły przyjmuje się, że jeżeli:
![]()
− to prognoza jest wysoce precyzyjna,
![]()
− to prognoza jest dostatecznie precyzyjna,
![]()
− to prognoza ma niedostateczną precyzję.
Należy jednak wyraźnie podkreślić, że o tym, czy prognozę przyjąć, czy też odrzucić decyduje jej odbiorca.
Zadanie 2.
Przewozy pasażerów transportem kolejowym w Polsce w latach 1997-2005 kształtowały się następująco:
Lata |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
Przewozy w mln osób |
416,6 |
400,8 |
395,2 |
360,2 |
331,8 |
304,1 |
283,0 |
272,0 |
258,0 |
Źródło: Rocznik Statystyczny GUS 2006
Przedstaw badany szereg graficznie.
Oszacuj parametry liniowego modelu trendu.
Oceń stopień dopasowania modelu do danych empirycznych.
Jakich przewozów można oczekiwać w 2007 roku?
Rozwiązanie:
ad a) Sporządzamy wykres szeregu:
Badane zjawisko charakteryzuje się wyraźnym spadkowym trendem rozwojowym. Wydaje się, że można przyjąć hipotezę, że jest to trend liniowy.
ad b) Hipotetyczny model trendu ma postać:
![]()
gdzie: t = 1, 2, ..., 9
W celu wyliczenia parametrów strukturalnych wykonujemy potrzebne obliczenia w tabeli roboczej:
Lata |
Przewozy w mln osób yt |
t |
|
t2 |
|
|
|
1997 1998 1999 2000 2001 2002 2003 2004 2005 |
416,6 400,8 395,2 360,2 331,8 304,1 283,0 272,0 258,0 |
1 2 3 4 5 6 7 8 9 |
416,6 801,6 1185,6 1440,8 1659,0 1824,6 1981,0 2176,0 2322,0 |
1 4 9 16 25 36 49 64 81 |
422,5 400,8 379,1 357,4 335,7 314,1 292,4 270,7 249,0 |
34,78 0,00 258,53 7,66 15,56 99,12 87,76 1,74 81,16 |
6537,62 4232,23 3534,96 598,07 15,56 1001,37 2781,98 4063,35 6044,20 |
X |
3021,7 |
45 |
13807,2 |
285 |
X |
586,31 |
28809,34 |
Oceny parametrów strukturalnych obliczamy korzystając ze wzorów:
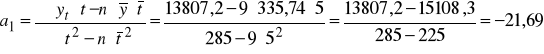
![]()
czyli:
![]()
Ocena parametru a1 informuje, że w latach 1997-2005 przewozy pasażerów w Polsce spadały przeciętnie rocznie o 21,69 mln osób.
Wartość a0 oznacza, że teoretycznie przewozy w 1996 roku, (czyli gdy t=0) wynosiły 444,19 mln osób.
ad c)
Obliczamy odchylenie standardowe składnika resztowego:
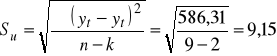
Rzeczywiste rozmiary przewozów w poszczególnych latach odchylają się od rozmiarów obliczonych na podstawie modelu trendu przeciętnie biorąc o +/- 9,15 mln osób.
Obliczamy błędy średnie szacunku ocen parametrów strukturalnych modelu:
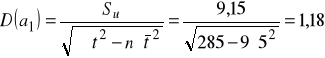
,
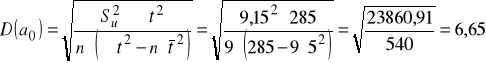
.
Ostatecznie więc funkcję trendu można zapisać w postaci:
![]()
.
Ocena a1 różni się od prawdziwej wartości parametru przeciętnie o +/- 1,18 mln osób, zaś ocena parametru a0 odchyla się od prawdziwej wartości parametru przeciętnie o +/- 6,65 mln osób.
Obliczamy współczynnik zgodności:
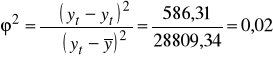
Oszacowany liniowy model trendu nie wyjaśnia 2,0 % zmienności badanego zjawiska w czasie.
Wyznaczony trend wykreślamy:
ad d) Zgodnie z przyjętą numeracją lat dla roku 2000 t = 11, stąd:
![]()
+/- 9,15
Jeżeli trend spadkowy przewozów z lat 1997-2005 utrzyma się nadal to w roku 2007 można oczekiwać przewozów 205,6 +/- 9,15 mln osób.
3
Wyszukiwarka
Podobne podstrony:
Analiza wahan sezonowych, materiały z roku 2011-2012, Semestr II, Statystyka opisowa - ćwiczenia
ANALIZA WSPOLZALEZNOSCI ZJAWISK czesc 1, materiały z roku 2011-2012, Semestr II, Statystyka opisowa
1Grupowanie, materiały z roku 2011-2012, Semestr II, Statystyka opisowa - ćwiczenia
Regresja liniowa dwoch zmiennych, materiały z roku 2011-2012, Semestr II, Statystyka opisowa - ćwicz
Wzory na 1 kolosa, UE ROND - UE KATOWICE, Rok 2 2011-2012, semestr 4, Finanse przedsiębiorstwa, Wykł
Program zajec pielegniarek 2011-2012 semestr II
Program zajec pielegniarek 2011 2012 semestr II
wzory statystyka opisowa (2011), Ekonomia UWr WPAIE 2010-2013, Semestr II, Statystyka Opisowa
11 Analiza Szeregów Czasowych z rozwiązaniami
Analiza szeregów czasowych wzory
11 Analiza Szeregów Czasowych
Analiza szeregów czasowych
analiza szeregow czasowych z9 i Nieznany (2)
więcej podobnych podstron